werken met exponentiële groei en de bijbehorende groeifactor, groeifactoren omrekenen;

lineaire groei en exponentiële groei vergelijken;

formules opstellen voor lineaire en exponentiële groei.

werken met lineaire en exponentiële groei;

de rekenregels voor machten gebruiken;

tabellen maken en grafieken tekenen bij formules van twee variabelen.

Door het uitvallen van een pomp die een bestrijdingsmiddel in een waterkringloop doseert, begin het aantal bacteriën in het water te groeien. Ieder uur verdubbelt het aantal bacteriën. Als de pomp uitvalt, zijn er $4,0 * 10^6$ bacteriën per kubieke meter water aanwezig. Als het waterfilter verstopt is, wordt het alarm geactiveerd.

Vul de onderstaande tabel in waarin het aantal bacteriën is uitgezet tegen de tijd.
Teken een bijpassende grafiek.

$t$ (uur)	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$
$A$ (aantal)	$4,0*10^6$	‌	‌	‌	‌	‌	‌	‌	‌

$t$ (uur)	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$
$A$ (aantal)	$4,0*10^6$	$8,0*10^6$	$16,0*10^6$	$32,0*10^6$	$64,0*10^6$	$1,28*10^8$	$2,56*10^8$	$5,12*10^8$	$10,24*10^8$

Zie figuur.

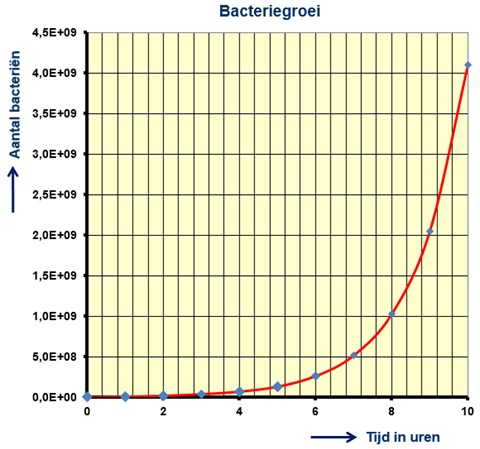
Hoe groot is de groeifactor per uur?

$2$

Geef een formule bij deze exponentiële groei, dus het verband tussen $A$ en $t$ , met $t$ in uren.

$A = 4,0*10^6*2^t$

Bij een aantal van $4,0 * 10^9$ bacteriën per kubieke meter water treedt er slijmvorming op waardoor het waterfilter verstopt raakt en er een alarm af gaat.

Na ongeveer hoeveel uur wordt het alarm geactiveerd?

Na ongeveer $10$ uur.

Als je een formule wilt maken met $t$ in minuten in plaats van in uren, zijn er twee mogelijkheden: groeifactor aanpassen of de exponent wijzigen. Het makkelijkste in dit geval is het wijzigen van de exponent.

Hoe ziet het verband tussen $A$ en $t$ er uit als $t$ in minuten wordt ingevuld?

$A = 4,0*10^6*2^(t/60)$

Controleer je formule door de uitkomst te bereken voor $t = 120$ minuten.

$A = 4,0*10^6*2^(120/60) = 16,0 * 10^6$ bacteriën.

Bereken hoeveel bacteriën er na $45$ minuten zijn.

$A = 4,0*10^6*2^(45/60) ~~ 6,73 * 10^6$ bacteriën.

Er zijn landen waarin de voetbalsport nog maar weinig beoefenaren kent, maar waarin die sport wel in opkomst is.

Stel dat in zo'n land A vanaf 1998 het aantal leden van voetbalclubs jaarlijks met $15000$ is toegenomen. Op 1 januari 2010 waren er $200000$ leden. Neem aan dat deze groei ongewijzigd door gaat.
Het aantal leden op 1 januari 2015 is dan $200000 + 15000 * 5 = 275000$ .
In dit geval is er sprake van lineaire groei, er komt jaarlijks een vast aantal leden bij.

In een andere opkomende voetbalnatie B neemt het aantal leden van voetbalclubs jaarlijks met $5$ % toe. Op 1 januari 2010 waren er $200000$ leden. Neem aan dat deze groei ongewijzigd door gaat.
Op 1 januari 2015 heeft dit land dan $200000 * 1,05^5 ~~ 255256$ , dus ongeveer $255000$ leden.
Nu spreek je van exponentiële groei met een beginhoeveelheid van $200000$ en een groeifactor van $1,05$ per jaar.

Je kunt voor beide manieren van groei formules en grafieken opstellen. Je noemt dan $A$ het aantal leden in land A, $B$ het aantal leden in land B en $t$ de tijd in jaren na 2010.

Bekijk in de Uitleg de groei van het aantal leden van voetbalclubs.

Welke formule kun je opstellen voor $A$ afhankelijk van $t$ ?

$A = 200000 + 15000 t$

Bereken het aantal leden van voetbalclubs in A in 2020 als de lineaire groei zo door blijft gaan.

$200000 + 15000*10 = 350000$

Stel een formule op voor $B$ afhankelijk van $t$ .

$B = 200000*1,05^t$

Bereken het aantal leden van voetbalclubs in B in 2020 als de exponentiële groei zo door blijft gaan.

$200000*1,05^10 ~~ 325779 ~~ 326000$

In B groeit het aantal leden van voetbalclubs met $5$ % per jaar.
Hoeveel procent per maand is dat?

De groeifactor per jaar ( $12$ maanden) is $1,05$ .
Noem je de groeifactor per maand $g$ , dan is $g*g*g*g*g*g*g*g*g*g*g*g = g^12 = 1,05$ .
De vergelijking $g^12 = 1,05$ kun je oplossen door de omgekeerde macht te gebruiken: $g = 1,05^(1/12) ~~ 1,004$ .
De maandelijkse groei is dus ongeveer $0,4$ %.

Bekijk opnieuw de groei van het aantal leden van voetbalclubs. Gebruik de formules bij de vorige opgave. Ga er van uit dat in beide landen de groei zo doorgaat.

Teken de grafieken van $A$ en $B$ in één figuur. Laat zien dat beide grafieken twee punten gemeenschappelijk hebben.

Maak eerst tabellen. Neem voor $t$ de waarden $0$ , $5$ , $10$ , $15$ en $20$ .

In welk jaar zijn er in land A meer leden van voetbalclubs dan in land B?

Maak je tabel nauwkeuriger. In 2027 zijn er in land B voor het eerst meer leden, namelijk ongeveer $458000$ terwijl er in land A dan $455000$ leden zijn.

Je ziet hier grafieken van twee belangrijke manieren van groei:

Lineaire groei met beginhoeveelheid $b$ en een vaste toename per eenheid van $a$ .
Bijbehorende formule: $H = a*t + b$ .
Bijbehorende grafiek: een rechte lijn door $(0, b)$ met hellingsgetal $a$ .

Exponentiële groei met beginhoeveelheid $b$ en een vaste groeifactor per eenheid van $g$ .
Bijbehorende formule: $H = b*g^t$ .
Bijbehorende grafiek: een steeds sterker stijgende curve door $(0, b)$ als $g gt 1$ en een steeds minder sterk dalende curve door $(0, b)$ als $0 lt g lt 1$ .

Bij lineaire groei met een vaste toename van $a=0$ spreek je van een constante functie.
En dat is ook het geval bij exponentiële groei met groeifactor $g^0 = 1$ .

Je kunt groeifactoren omrekenen:
als de groeifactor per dag $1,5$ is, dan is hij per week $1,5^7$ en per uur $1,5^(1/24)$ .

Na jaren van terugloop is de populatie zeehonden in het Nederlandse deel van het Waddengebied gelukkig weer gestegen. Sinds juni 2008 is het aantal zeehonden in dit gebied maandelijks met $2,6$ % toegenomen. Ga ervan uit dat er op 1 juli 2008 $1534$ zeehonden waren.
Neem aan dat de groei van het aantal zeehonden in dit gebied een tijdlang zo doorgaat en stel een bijpassende formule op.
Bereken het aantal zeehonden op 1 januari 2013.

Omdat er per maand een vast percentage zeehonden bij komt, is er sprake van exponentiële groei. De groeifactor per maand is $1,026$ . Neem $t = 0$ op 1 juli 2008, dan is de beginhoeveelheid $1534$ .
Is het aantal zeehonden $Z$ en de tijd in maanden $t$ dan is een juiste formule $Z = 1534*1,026^t$ .

Voor het aantal zeehonden op 1 januari 2013 geldt nu $t = 54$ . Vul je dit in de formule in, dan vind je $Z ~~ 6135$ .

In Voorbeeld zie je hoe de populatie zeehonden in het Nederlandse deel van de Waddenzee groeit.

Bereken het aantal zeehonden op 1 januari 2009.

$1534*1,026^6 ~~ 1789$

Hoeveel bedraagt de groeifactor per jaar? En het groeipercentage?

$1,026^12 ~~ 1,361$ en dat is een groeipercentage van ongeveer $36,1$ % per jaar.

Stel een formule op voor het aantal zeehonden $Z$ afhankelijk van de tijd $t$ in jaren. Neem $t = 0$ op 1 januari 2009.

$Z = 1789*1,361^t$

Bereken ook met de formule die je in c hebt gevonden het aantal zeehonden op 1 januari 2013. Verklaar het kleine verschil.

Je vindt nu ongeveer $6138$ zeehonden. Het verschil komt door de afrondingen.

In de Theorie zie je een applet waarin grafieken van lineaire groei en exponentiële groei met dezelfde beginhoeveelheid worden vergeleken.

Stel de functies $H_1 = 4*1,10^t$ en $H_{2} = 0,6 t + 4$ in met behulp van de schuifbalkjes. Hoeveel snijpunten hebben de grafieken van deze functies?

Doen, er zijn twee snijpunten.

Het éne snijpunt is uiteraard $(0, 4)$ . Bepaal het tweede snijpunt in één decimaal nauwkeurig.

Maak zelf de grafieken in GeoGebra en laat dit programma het snijpunt bepalen, of gebruik een grafische rekenmachine. Je vindt $(8, 9)$ .

Als je de groeifactor van $H_{1}$ verandert, hebben de grafieken soms nog maar één snijpunt. Moet je de groeifactor daartoe groter of kleiner maken?

Dit lukt alleen als de groeifactor groter wordt. Vanaf een groeifactor van ongeveer $1,17$ .

Stel de functies $H_1 = 4*0,80^t$ en $H_{2} = - 0,5 t + 4$ in met behulp van de schuifbalkjes. Hoeveel snijpunten hebben de grafieken van deze functies?

Doen, ook nu zijn er twee snijpunten.

Het éne snijpunt is uiteraard $(0, 4)$ . Bereken met behulp van inklemmen het tweede snijpunt in één decimaal nauwkeurig.

Maak zelf de grafieken in GeoGebra en laat dit programma het snijpunt bepalen, of gebruik een grafische rekenmachine. Je vindt $(5,8; 1,1)$ .

De afdeling bevolking van de gemeente Amsteldijk verwacht dat er eind van dit jaar zo’n $40.000$ mensen in deze gemeente zullen wonen. Het gemeentebestuur hoopt dat het inwonersaantal nog verder zal uitbreiden omdat dit de mogelijkheid biedt om enkele voorzieningen te verbeteren.
Wethouder Simonsz zegt: We streven er naar om elk jaar $1500$ inwoners meer te hebben.
De burgemeester mw. Jansma hoopt echter elk jaar $3$ % meer inwoners te kunnen inschrijven dan het jaar ervoor.

Maak nu grafieken voor de bevolkingsgrootte voor de komende acht jaar. Eén die past bij de uitspraak van dhr. Simonsz en één die past bij de uitspraak van mw. Jansma.

Tijd $t$	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$
Aantal vlg Simonsz	$40000$	$41500$	$43000$	$44500$	$46000$	$47500$	$49000$	$50500$	$52000$
Aantal vlg Jansma	$40000$	$41200$	$42436$	$43709$	$45020$	$46371$	$47762$	$49195$	$50671$

Geef een passende formule voor het aantal inwoners $N$ afhankelijk van de tijd $t$ in jaren die past bij de uitspraak van wethouder Simonsz. Ga er van uit dat op $t = 0$ het aantal inwoners $40000$ is.

$N = 40000 + 1500 t$

Geef een passende formule voor het aantal inwoners $N$ afhankelijk van de tijd $t$ in jaren die past bij de uitspraak van burgemeester Jansma. Ga er van uit dat op $t = 0$ het aantal inwoners $40000$ is.

$N = 40000 * 1,03^t$

Welk van beide formules levert op den duur de meeste inwoners op voor de gemeente Amsteldijk? Licht je antwoord toe.

Op den duur zal de formule van mw. Jansma de meeste inwoners opleveren. Bij haar formule komt er jaarlijks een steeds groter aantal bij.

Volgens welke formule is het aantal inwoners van Amsteldijk voor het eerst verdubbeld?

Verdubbeling bij Simonsz: $40000 + 1500 t = 80000$ geeft met de balansmethode $t ~~ 26,7$ jaar.
Verdubbeling bij Jansma: $40000 * 1,03^t = 80000$ geeft met behulp van GeoGebra of een grafische rekenmachine $t ~~ 23,4$ jaar.
Volgens de formule van mw. Jansma is het aantal inwoners het eerst verdubbeld.

In deze tabel wordt de groei van het aantal inwoners (afgerond op honderdtallen) van twee steden A en B weergegeven. Bij stad A is bij benadering sprake van lineaire groei en bij stad B heb je meer te maken met exponentiële groei. In welk jaar gaat het aantal inwoners van B dat van A overschrijden als de groei zo door gaat?

jaartal	2000	2001	2002	2003	2004	2005	2006	2007	2008
aantal inwoners A	$79600$	$81100$	$82600$	$84200$	$85600$	$87100$	$88500$	$90100$	$91600$
aantal inwoners B	$72100$	$73900$	$75800$	$77600$	$79600$	$81600$	$83600$	$85700$	$87800$

In stad A is de groei ongeveer lineair, er komen jaarlijks ongeveer $1500$ mensen bij. Er geldt $A = 79600 + 1500 t$ waarin $A$ het aantal inwoners van A en $t$ de tijd in jaren na 2000 is.

In stad B is de groei ongeveer exponentieel met groeifactor $1,025$ . Er geldt $B = 72100*1,025^t$ waarin $B$ het aantal inwoners van A en $t$ de tijd in jaren na 2000 is.

Met behulp van deze formules kun je de tabellen voortzetten. Je merkt dan dat vanaf 2013 stad B meer inwoners heeft dan stad A.

Bekijk Voorbeeld.

Hoe ga je na dat er voor stad A (ongeveer) sprake is van lineaire groei? Ga dit ook echt na.

Je trekt telkens de aantallen inwoners van twee opeenvolgende jaren van elkaar af. Daar komt steeds ongeveer $1500$ uit. De getallen verschillen wel wat van jaar tot jaar, maar gemiddeld klopt dit wel ongeveer. In een grafiek ziet het er ook redelijk uit als een rechte lijn.

Hoe leid je voor stad A de formule af uit de tabel?

De beginhoeveelheid is $79600$ op $t = 0$ en er komen jaarlijks ongeveer $1500$ inwoners bij.

Hoe ga je na dat er voor stad B (ongeveer) sprake is van exponentiële groei? Ga dit ook echt na.

Je deelt telkens de aantallen inwoners van twee opeenvolgende jaren op elkaar. Daar komt steeds ongeveer $1,025$ uit. De getallen kunnen wel wat van jaar tot jaar verschillen, maar gemiddeld klopt dit wel ongeveer. In een grafiek zie je de steeds sterkere stijging.

Hoe leid je voor stad A de formule af uit de tabel?

De beginhoeveelheid is $72100$ op $t = 0$ en er is een groeifactor per jaar van ongeveer $1,025$ .

Laat zien in welk jaar het aantal inwoners van B dat van A gaat overschrijden als de groei zo door gaat.

Maak de tabellen verder af, of werk met GeoGebra of een grafische rekenmachine.

Hier zie je een grafiek die laat zien hoe een hoeveelheid gif $G$ (in mg/L) in het water wordt afgebroken. De eerste drie metingen staan in de figuur. De hoeveelheid gif wordt steeds ongeveer met eenzelfde factor vermenigvuldigd die kleiner is dan $1$ , dus de hoeveelheid wordt steeds minder. Je spreekt dan van exponentieel verval.

Laat met een berekening zien, dat er (ongeveer) sprake is van exponentieel verval.

Na het eerste uur is nog $\frac{51}{60} = 0,85$ deel over, na het tweede uur nog $\frac{43}{51} \approx 0,84$ en na het derde uur ook nog $\frac{37}{43} = 0,86$ . Gemiddeld is er een groeifactor van $0,85$ .

Leid een formule af voor $G$ afhankelijk van $t$ .

$G = 60 \cdot {0,85}^{t}$

Na hoeveel uur is er minder dan $1$ % van deze giftige stof over?

Maak een tabel. Na $15$ uur is dit het geval.

Van een hoeveelheid $N$ is het volgende gegeven:
Op $t = 3$ is $N = 1200$ en op $t = 11$ is $N = 800$ .

Stel een formule op voor $N$ als functie van $t$ er sprake is exponentiële groei.

Bij exponentiële groei is er sprake van een groeifactor $g$ per tijdseenheid. Per $8$ tijdseenheden vermenigvuldig je met $800 / 1200 = \frac{2}{3}$ . Je moet daarvoor acht keer met de groeifactor $g$ vermenigvuldigen, dus $g \cdot g \cdot g \cdot g \cdot g \cdot g \cdot g \cdot g = g^{8} = \frac{2}{3}$ .
Je vindt $g = (2/3)^(1/8) ~~ 0,95$ .
Merk daarbij op dat het gebruikelijk is om de groeifactor (tenzij anders wordt vermeld) in twee decimalen, dus in procenten, nauwkeurig te bepalen.

De gevraagde formule is nu $N = b \cdot {0,95}^{t}$ .
Om de juiste waarde voor de beginhoeveelheid $b$ te vinden gebruik je bijvoorbeeld $t = 3$ en $N = 1200$ . Je vindt dan $b \approx 1400$ .

De formule wordt $N \approx 1400 \cdot {0,95}^{t}$ .

Bekijk hoe in Voorbeeld een formule voor exponentiële groei van een hoeveelheid $N$ wordt gevonden op basis van de waarden van $N$ op twee verschillende tijdstippen.

Bereken zelf de groeifactor per tijdseenheid.

$g = \sqrt[8]{\frac{2}{3}} \approx 0,95$

Voer ook zelf de berekening van de beginhoeveelheid uit.

Uit $1200 = b \cdot {0,95}^{3}$ volgt $b \approx 1400$ .

Je kunt de beginhoeveelheid ook berekenen door op $t = 11$ is $N = 800$ te gebruiken. Laat zien dat je ongeveer op hetzelfde uitkomt.

Uit $800 = b \cdot {0,95}^{11}$ volgt $b \approx 1406$ . Het verschil zit hem in de afronding van de groeifactor.

Bij de gegevens in Voorbeeld past ook een lineaire formule voor $N$ als functie van $t$ .

Stel zo'n bijpassende formule op.

Per $11 - 3 = 8$ tijdseenheden is er een afname van $1200 - 800 = 400$ . Per tijdseenheid dus een afname van $50$ .
Bij deze lineaire functie past een formule van de vorm $N = - 50 t + b$ . Nog even $t = 3$ en $N = 1200$ invullen en je krijgt de formule $N = - 50 t + 1350$ .

Je hebt nu twee rekenmodellen bij dezelfde gegevens: een lineaire functie en een exponentiële functie. Maar ze verschillen nogal.

Bereken bij beide rekenmodellen de waarde van $N$ als $t = 20$ .

Lineaire functie: $N = - 50 \cdot 20 + 1350 = 350$ .
Exponentiële functie: $N = 1400 \cdot {0,95}^{20} \approx 502$

Bij de lineaire functie is de hoeveelheid $N$ op zeker moment op. Op welk moment is dat? En hoe zit het dan met het exponentiële rekenmodel?

Uit $- 50 t + 1350 = 0$ volgt $t = 27$ . Het exponentiële groeimodel geeft dan $N \approx 350$ .

Is bij de exponentiële functie de hoeveelheid $N$ ook op zeker moment op? Licht je antwoord toe.

Eigenlijk raakt de hoeveelheid $N$ nooit op, elke keer is er nog $95$ % van de vorige hoeveelheid over. Maar op zeker moment zal de hoeveelheid zo klein zijn dat hij niet meer waarneembaar of meetbaar is.

Een hoeveelheid $H$ heeft op $t = 0$ de waarde $160$ . Stel in de volgende gevallen een formule op voor $H$ afhankelijk van $t$ (in dagen) en bereken de waarde van $H$ op $t = 10$ in gehelen nauwkeurig.

$H$ neemt dagelijks toe met $15$ %.

$H = 160 \cdot {1,15}^{t}$ en op $t = 10$ geldt $H \approx 647$ .

$H$ neemt dagelijks toe met $15$ .

$H = 160 + 15^{t}$ en op $t = 10$ geldt $H \approx 310$ .

$H$ neemt dagelijks af met $15$ %.

$H = 160 \cdot {0,85}^{t}$ en op $t = 10$ geldt $H \approx 31$ .

$H$ neemt dagelijks af met $15$ .

$H = 160 - 15^{t}$ en op $t = 10$ geldt $H \approx 10$ .

$H$ neemt wekelijks toe met $15$ %.

De groeifactor per dag bereken je uit $g^{7} = 1,15$ . Je vindt $g \approx 1,02$ .
De formule is dan $H = 160 \cdot {1,02}^{t}$ en op $t = 10$ geldt $H \approx 195$ .

$H$ neemt wekelijks af met $15$ %.

De groeifactor per dag bereken je uit $g^{7} = 0,85$ . Je vindt $g \approx 0,977$ .
De formule is dan $H = 160 \cdot {0,977}^{t}$ en op $t = 10$ geldt $H \approx 127$ .

Van een middelgrote stad geeft deze tabel de aantallen inwoners afgerond op honderdtallen. Op de afdeling huisvesting wil men de groei voor de komende jaren voorspellen.

jaartal	bevolking
2008	154000
2009	156300
2010	158700
2011	161000

Eén van de medewerkers zegt: Je zou kunnen veronderstellen dat er jaarlijks zo'n 2300 inwoners bijkomen.

Van welke soort groei gaat deze medewerker uit? Laat zien dat dit wel ongeveer zou kunnen kloppen binnen de afgesproken afronding.

Deze medewerker gaat uit van lineaire groei. Als je begint met $154000$ inwoners in 2008 en je telt daar elk volgend jaar $2300$ inwoners bij, dan krijg je voor 2009 precies $156300$ , voor 2010 $158600$ en voor 2011 $160900$ inwoners. En dat zou alleen aan de afrondingen kunnen liggen.

Neem aan dat $t$ de tijd in jaren na 2008 is. Welke formule voor het aantal inwoners $I$ volgt uit de aanname van lineaire groei?

$I = 2300 t + 154000$

Een andere medewerker merkt op: Er zou ook sprake kunnen zijn van exponentiële groei met 1,5% per jaar.

Laat zien hoe zij aan dit groeipercentage is gekomen.

$156300 / 154000 \approx 1,015$ , $158700 / 156300 \approx 1,015$ en $161000 / 158700 \approx 1,015$ . Er is dus een groeifactor van $1,015$ per jaar.

Welke formule kun je opstellen voor $I$ als functie van $t$ uitgaande van deze exponentiële groei?

$I = 154000 \cdot {1,015}^{t}$

Er zijn nu twee formules gevonden waarmee je de bevolking van deze stad in volgende jaren zou kunnen voorspellen. Wat is het grote verschil tussen beide?

Bij de exponentiële groei wordt de jaarlijkse stijging van het aantal inwoners steeds groter, dus worden op den duur de bevolkingsaantallen erg groot. Bij lineaire groei is de stijging jaarlijks gelijk.

Voorspel met beide formules het aantal inwoners van deze stad in 2020.

Lineaire groei: $I = 2300 \cdot 12 + 154000 = 181600$ .
Exponentiële groei: $I = 154000 \cdot {1,015}^{12} \approx 184100$ .

In een uiterwaard langs de IJssel heeft Rijkswaterstaat in 2005 vossen uitgezet om het aantal konijnen dat er leeft te doen verminderen. De konijnen vormden namelijk een plaag in dit gebied. Biologen hebben sinds 2005 jaarlijks het aantal konijnen geteld. Dit is weergegeven in de volgende tabel:

jaartal	2005	2006	2007	2008	2009
aantal konijnen	$1450$	$1261$	$1097$	$954$	$830$

Met hoeveel procent per jaar neemt het aantal konijnen sinds 2005 af? Is dat percentage elk jaar ongeveer evenveel?

Als je de opeenvolgende aantal vossen steeds op elkaar deelt, vind je telkens ongeveer $0,87$ . De konijnen verminderen dus elk jaar ongeveer $13$ % in aantal.

Welke formule kun je opstellen voor het aantal konijnen $K$ afhankelijk van de tijd $t$ in jaren?

$N = 1450*0,87^t$ .

Het aantal konijnen mag echter niet onder de $175$ komen, want dan loopt hun voortbestaan gevaar en hebben ook de vossen niet meer voldoende voedsel.

Vanaf welk jaar moet Rijkswaterstaat beginnen met het vangen van vossen om te voorkomen dat dit gebeurt?

Maak de tabel verder af, of gebruik GeoGebra of een grafische rekenmachine.
Vanaf 2020 komt het aantal konijnen vlak bij de $175$ , dus dan moet het aantal vossen wel worden verkleind.

Als je gaat duiken in de diepzee dan zul je merken dat hoe dieper je komt, hoe blauwer alles eruit ziet. Dit komt doordat het rode licht minder ver in water doordringt dan blauw licht. Dit blauwe licht kan dan dieper doordringen. Per meter diepte wordt $32,7$ % van het blauwe licht tegengehouden door het water.

Tot welke diepte dringt dan nog maar $1$ % van het blauwe licht door?

Per meter wordt $32,7$ % tegengehouden en dus dringt er $67,3$ % door. De groeifactor waar je mee rekent is dus $0,673$ . Neem $100$ als beginhoeveelheid en los op:

$100 \cdot {0.673}^{t} = 1$

Maak een tabel en je merkt dat je tot iets minder dan $12$ m diepte nog meer dan $1$ % blauw licht hebt.

Elke ochtend om 9:00 uur krijgt een patiënt door middel van een injectie $2$ mL van een pijnstillend medicijn toegediend. Door afbraak in het lichaam van de patiënt neemt de hoeveelheid geneesmiddel elke $12$ uur af met $32$ %.

Met welke groeifactor neemt de hoeveelheid pijnstiller elke $12$ uur af?

$0,68$ .

Met welke groeifactor neemt de hoeveelheid pijnstiller elke $6$ uur af? Welk afnamepercentage per zes uur hoort daar bij?

Noem die groeifactor $g$ , dan is $g^{2} = 0,68$ . En dus is $g = \sqrt{0,68} \approx 0,82$ . Dat is een afname van ongeveer $18$ % per zes uur.

Met welke groeifactor neemt de hoeveelheid pijnstiller elk uur af? Welk afnamepercentage per uur hoort daar bij?

Noem die groeifactor $g$ , dan is $g^{12} = 0,68$ en $g = \sqrt[12]{0,68} \approx 0,97$ . Dat is een afname van ongeveer $3$ % per uur.

Hoeveel mL van het pijnstillend middel bevindt zich na één dag vlak voor de volgende injectie in het lichaam van de man? En hoeveel mL direct na de injectie?

Nog $0,92$ mL vlak voor de injectie en dus $2,92$ mL vlak erna.

Bereken de hoeveelheid pijnstiller na $30$ uur. En ook na $60$ uur.

Na $30$ uur: $2,92 \cdot 0,82 \approx 2,39$ mL.
Aan het einde van de tweede dag (dus na $48$ uur) heeft de patiënt nog $2,92 \cdot {0,68}^{2} \approx 1,35$ mL pijnstiller in zijn lichaam. Na een derde injectie wordt dit $3,35$ mL.
Na $60$ uur heeft hij $3,35 \cdot 0,68 \approx 2,28$ mL pijnstiller in zijn lichaam.

Schets een grafiek van de hoeveelheid geneesmiddel gedurende de eerste $60$ uur.

Doen, je krijgt een grafiek met verticale sprongen. Gebruik de gegevens uit deze opgave.

Een dergelijke grafiek stond eind 2011 in De Volkskrant. Men dacht op dat moment dat het aantal mensen op Aarde de $7$ miljard was overschreden. De grafiek doet sterk denken aan exponentiële groei. Toch is dat niet helemaal juist.

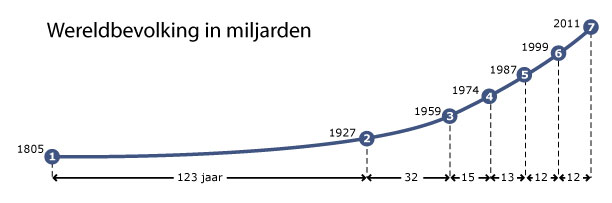
Laat zien dat de wereldbevolking tussen 1805 en 1927 met ongeveer $0,56$ % per jaar toenam.

$1 \cdot {1,0056}^{123} \approx 2$

Tussen 1927 en 1959 groeide de wereldbevolking sneller.

Met hoeveel procent per jaar ongeveer?

$1,5^(1/32) ~~ 1,0128$ .
Je vindt dus ongeveer $1,28$ % per jaar.

Laat zien dat de wereldbevolking tussen 1959 en 1974 het snelst groeide en dat de groei daarna weer wat afnam.

Tussen 1959 en 1974 was de groei ongeveer $1,94$ % per jaar. Daarna was de groei van 1974 tot 1987 ongeveer $1,73$ % per jaar, van 1987 tot 1999 ongeveer $1,53$ % per jaar en van 1999 tot 2011 ongeveer $1,29$ % per jaar.

Als de groei de komende jaren op dezelfde wijze zal doorgaan, wat betekent dit dan voor de wereldbevolking op den duur?

De wereldbevolking zal dan nog een tijd blijven stijgen, maar wel met een steeds kleiner percentage.

Als er iets is dat steeds sneller lijkt te groeien dan is dat wel het computergebruik en het internetverkeer. Het plaatje hiernaast laat daar iets van zien uit de beginjaren van het computertijdperk waarin we nu leven. De tabel symboliseert de wet van Moore. Daarbij moet je weten dat de zogenaamde processor (een minuscuul printplaatje, een chip) de hele rekenkracht van de computer vertegenwoordigde. Daarbij speelde het aantal transistoren dat men op zo'n processor kwijt kon een grote rol: hoe meer processoren, hoe groter de rekenkracht. In 1970 voorspelde Gordon Moore (één van de oprichters van chipsfabrikant Intel) dat het aantal transistoren dat men op zo'n processor kwijt kon elke $2$ jaar zou verdubbelen. En hij kreeg gelijk...
Na 2000 werden er meerdere processoren gebruikt die samen de rekencapaciteit nog verder konden verhogen. Pas in de huidige tijd wordt er gewerkt aan andere technologieën voor computers en zal de wet van Moore wellicht ooit in het museum terecht komen.

Maar niet alleen de rekenkracht van de computer groeide exponentieel, ook het aantal gebruikers van internet, van Google, van Facebook, ..., groeide enorm. En het is niet duidelijk of de grenzen van die groei in zicht komen...

De wet van Moore

Bekijk de figuur.

In 1972 introduceerde Intel de 8008 processor met $2500$ transistoren. Ga uit van de wet van Moore dat elke $2$ jaar het aantal transistoren op een processor verdubbelt.

In 1993 introduceerde Intel de Pentium-processor. Lag men met die processor nog op Moore's schema?

$2500 \cdot 2^{10,5} \approx 3620387$ . Dat zijn meer dan $3,6 \cdot 10^{6}$ transistoren. Dat is iets meer dan in de tabel.

In 2000 kwam de Pentium 4. Paste die in de wet van Moore?

$2500 \cdot 2^{14} \approx 40960000$ . Dat zijn bijna $41 \cdot 10^{6}$ transistoren. En ook dat lijkt te kloppen met de tabel.

Zeker tot 2012 is de rekenkracht van een computer ongeveer elke twee jaar verdubbeld. Stel je voor dat $R$ die rekenkracht voorstelt afhankelijk van $t$ het aantal jaren na 1972. Op $t = 0$ is $R = 2500$ .

Stel een formule op voor $R$ als functie van $t$ .

$R = 2500 \cdot {1,414}^{t}$

Bereken hiermee de rekenkracht die een computer uit 2012 volgens de wet van Moore zou hebben.

$R = 2500 \cdot {1,414}^{40} \approx 2,6 \cdot 10^{9}$

Onderzoek in welk jaar die rekenkracht boven de $1$ biljoen, dus boven $1 \cdot 10^{12}$ uit gaat komen volgens de wet van Moore.

Maak een tabel bij de formule die je hebt gemaakt. Je vindt dat dit omstreeks 2029 het geval zou moeten zijn.

Pasteurisatie

Bij pasteurisatie wordt een vloeistof verwarmd om de bacteriën in de vloeistof te doden. In een vloeistof bevinden zich $100text(.)000$ ( $= 10^5$ ) bacteriën die door pasteurisatie worden gedood. Bij het toegepaste pasteurisatieproces wordt per $20$ seconden het aantal bacteriën gehalveerd.

Vul deze tabel verder in.

$t$ (seconden)	$0$	$20$	$40$	$60$	$80$
$A$ (aantal)	$100text(.)000$	‌	‌	‌	‌

$t$ (seconden)	$0$	$20$	$40$	$60$	$80$
$A$ (aantal)	$100text(.)000$	$50text(.)000$	$25text(.)000$	$12text(.)500$	$6250$

Geef een schatting na hoeveel seconden het aantal bacteriën onder de $1000$ komt.

Na ongeveer $140$ s.

Bij het verband tussen het aantal bacteriën ( $A$ ) en de tijd ( $t$ ) in minuten van bovenstaand pasteurisatieproces past de formule:

$A = 100text(.)000*(1/8)^t$

Leg de formule eens uit.

Per minuut wordt er $3$ keer met $1/2$ vermenigvuldigd en wordt dus het aantal bacteriën met $1/2 * 1/2 * 1/2 = 1/8$ vermenigvuldigd.

Bereken het aantal bacteriën na $4$ minuten. Rond je antwoord af op een heel aantal.

$100text(.)000 * (1/8)^4 ~~ 24$ bacteriën.

Beredeneer hoeveel bacteriën er nog na $4$ minuten zouden zijn als bij de pasteurisatie het aantal bacteriën iedere $30$ seconden zou halveren (i.p.v. iedere $20$ seconden).

Per minuut wordt nu $2$ keer met $1/2$ vermenigvuldigd en wordt dus de groeifactor per minuut $1/2 * 1/2 = 1/4$ . Je hebt dan na $4$ minuten nog $100text(.)000 * (1/4)^4 ~~ 391$ bacteriën.

Leeglopen vloeistofvat

Een met vloeistof gevuld vat zal steeds langzamer leeglopen omdat de hoogte van de vloeistof afneemt waardoor de druk op de uitstroomopening afneemt. Het verloop is in onderstaande grafiek weergegeven. Hierin is $H$ de waterhoogte in cm en $t$ de tijd in seconden.

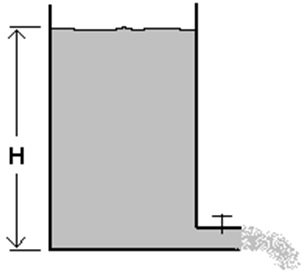
Bepaal met behulp van de grafiek de halveringstijd van de vloeistofhoogte.

$5$ s.

Voor het verband tussen $H$ en $t$ geldt:

$H = H_0*(1/2)^(t/(tau_1))$

Hierin is $H_0$ de waterhoogte op $t=0$ .

Bepaal $H_0$ en $tau_1$ en geef de ingevulde formule.

$H = 30*(1/2)^(t/5)$

Leg met behulp van de formule uit dat $tau_1$ de tijd is waarbij de vloeistofhoogte is gehalveerd. En leg ook uit dat na $2*tau_1$ seconden de vloeistofhoogte nog maar een kwart van de oorspronkelijke hoogte is.

Als je $t = tau_1 = 5$ invult komt er $H = 30*(1/2)^(5/5) = 30*(1/2)^1$ en halveert de beginhoeveelheid.

Als je $t = 2*tau_1 = 10$ invult komt er $H = 30*(1/2)^(10/5) = 30*(1/2)^2 = 30* 1/4$ en wordt de beginhoeveelheid door $4$ gedeeld.

Bereken na hoeveel seconden de vloeistofhoogte $6$ cm bedraagt. Geef je antwoord in twee decimalen nauwkeurig.

$H = 30*(1/2)^(t/5) = 6$ geeft (gebruik GeoGebra, Desmos of een GR) $t ~~ 13,06$ s.

De uitstroomopening wordt vernauwd en de bak loopt opnieuw leeg.
Voor $t=10$ s geldt $H=10$ cm.
De beginhoogte blijft hetzelfde. Nu geldt:

$H = H_0*(1/3)^(t/(tau_2))$

Bepaal $H_0$ en $tau_2$ en geef de ingevulde formule.

$H = 30*(1/3)^(t/10)$

Henri beweert dat de formule van de vorige opdracht, met de vernauwde uitstroomopening, ook anders geschreven kan worden. Hij komt met de volgende formule:

$H = 30*3^(text(-)0,1t)$

Laat zien dat deze formule (ook) klopt. Doe dit op twee manieren: door te onderzoeken of de formule dezelfde uitkomsten geeft én door de formule te herleiden.

Maak bij beide formules de grafieken. Ze zullen samenvallen.

Herleiden: $H = 30*(1/3)^(t/10) = 30*(3^(text(-)1))^(0,1t) = 30*3^(text(-)0,1t)$ .

Autobanden zijn meestal een beetje poreus (luchtdoorlatend). Dit betekent dat een opgepompte band steeds een beetje zachter wordt. De bandenspanning van een band is na het oppompen ongeveer gelijk aan $2,103$ bar. Deze bandenspanning neemt elke dag met ongeveer $13,3$ % af.

Welke groeifactor per dag heeft de bandenspanning?

$0,867$

Welke groeifactor per week heeft de bandenspanning? En welke groeifactor per uur?

Per week: ${0,867}^{7} \approx 0,368$ .
Per uur: $0,867^(1/24) ~~ 0,988$ .

Stel een formule op voor de bandenspanning $p$ van deze autoband afhankelijk van de tijd $t$ in dagen.

$p = 2,103*0,867^t$

Je kunt niet meer rijden als de bandenspanning minder is dan $0,1$ bar. Hoeveel dagen duurt dit nadat je de band hebt opgepompt?

Maak een tabel of gebruik de formule en GeoGebra of een grafische rekenmachine. Voor het eerst op de $22$ ste dag, dus het duurt $21$ dagen.

Het aantal WhatsApp-berichten $W$ is sinds 2001 flink toegenomen. Zie onderstaande tabel (aantallen berichten $W$ in miljoenen):

jaartal	2005	2006	2007	2008
$W$	$4,9$	$9,8$	$19,6$	$39,2$

Met hoeveel procent neemt het aantal WhatsApp-berichten per jaar toe?

Met groeifactor $2$ , dus met $100$ % per jaar.

Welke formule kun je opstellen voor het aantal WhatsApp-berichten $W$ per jaar (in miljoenen) afhankelijk van het aantal jaren $t$ na 2005?

$W = 4,9*2^t$

Hoeveel van deze berichten verwachtte men in 2012?

$39,2 \cdot 2^{4} = 627,2$ mln.