de omtrek en de oppervlakte van veelhoeken berekenen;
werken met formules voor de oppervlakte van driehoeken en vierhoeken.
vlakke figuren, met name driehoeken en vierhoeken en hun eigenschappen;
lengtes van zijden in driehoeken berekenen met de stelling van Pythagoras en/of gelijkvormigheid.
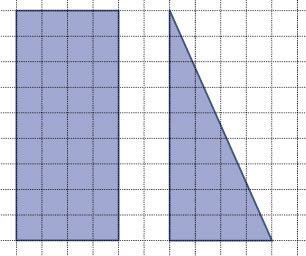
Je ziet hier een rechthoek en een rechthoekige driehoek op een cm-rooster.
Hoeveel cm
cm
Hoeveel cm
cm
Precies de helft van de oppervlakte van de rechthoek, dus
cm
Waarom kun je van deze figuren gemakkelijk de oppervlakte bepalen?
Ze staan op een cm-rooster en de hoekpunten zijn roosterpunten. Bovendien zijn het rechthoeken (of handige delen ervan).
Ze staan op een cm-rooster en de hoekpunten zijn roosterpunten. Bovendien zijn het rechthoeken (of handige delen ervan).
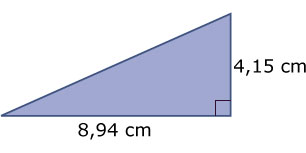
Dit is een rechthoekige driehoek die niet precies op een cm-rooster past.
Waarom moet nu het rechtehoekteken in de figuur staan?
Omdat je niet zeker weet of de hoek een rechte hoek is. Dat zie je alleen wanneer de driehoek in een rooster staat (waarvan je aanneemt dat de roosterlijnen loodrecht op elkaar staan).
Omdat je niet zeker weet of de hoek een rechte hoek is. Dat zie je alleen wanneer de driehoek in een rooster staat (waarvan je aanneemt dat de roosterlijnen loodrecht op elkaar staan).
Hoeveel cm
cm
Het is precies de helft van de oppervlakte van een rechthoek met zijden van
bij cm. De oppervlakte is daarom
cm
Hoe reken je in het algemeen de oppervlakte uit van een rechthoekige driehoek? Probeer je antwoord in formulevorm te geven.
Noem de rechthoekszijden
Om de oppervlakte van een figuur te bepalen kun je soms handig gebruikmaken van oppervlakteformules.
De oppervlakte van een rechthoek kun je berekenen met
Noem je de lengte en de breedte , dan geldt de formule:
Voor de oppervlakte van de rechthoekige driehoek, geldt:
Voor de oppervlakte van een vierkant (dus
Van figuren met andere vormen kun je ook de oppervlakte uitrekenen:
Is de figuur uit bekende basisvormen opgebouwd, dan kun je eerst de oppervlakte van deze basisvormen berekenen. Daarna tel je die oppervlaktes bij elkaar op.
Je kunt ook een rechthoek om een figuur heen maken. Bereken daar de oppervlakte van. Vervolgens trek je daar de oppervlakte van de
Bekijk de drie rechthoeken en rechthoekige driehoek.
Waarom moet je de oppervlakte van deze figuren berekenen met behulp van een oppervlakteformule?
Omdat je geen
Bereken van elk van deze vier figuren de exacte oppervlakte.
Figuur a: cm
Figuur b: cm
Figuur c: cm
Figuur d: cm
Figuur a: cm
Figuur b: cm
Figuur c: cm
Figuur d: cm
Van een rechthoek kun je gemakkelijk de omtrek berekenen. Welke formule geldt voor de omtrek van een rechthoek?
Of:
Met haakjes is het nog korter:
Bereken de exacte omtrek van de figuren a, b en c.
Figuur a: cm
Figuur b: cm
Figuur c: cm
Figuur a: cm
Figuur b: cm
Figuur c: cm
Hoe kun je van figuur d de omtrek bepalen?
Door eerst met behulp van de stelling van Pythagoras de hypothenusa te berekenen: . Vervolgens kun je de lengtes van de drie zijden optellen. De omtrek wordt .
Door eerst met behulp van de stelling van Pythagoras de hypothenusa te berekenen: . Vervolgens kun je de lengtes van de drie zijden optellen. De omtrek wordt .
In de uitleg vind je de oppervlakteformule voor een vierkant.
Bereken de exacte oppervlakte van een vierkant met zijden van mm.
mm
Bereken de lengte van de zijde van een vierkant met een oppervlakte van mm
mm
geeft mm. De zijde van dit vierkant is dus ongeveer mm.
Welke formule geldt voor de omtrek van een vierkant met zijde ?
Bekijk figuur a en b. De roostereenheid is cm.
Bereken de exacte oppervlakte van figuur a in cm
Deze figuur is te zien als een samenstelling van rechthoek I en de driehoeken II en III. Er geldt:
Deze figuur is te zien als een samenstelling van rechthoek I en de driehoeken II en III. Er geldt:
Bereken de oppervlakte van figuur b in cm
Zet een rechthoek van cm bij cm om figuur b. De oppervlakte van de figuur is de oppervlakte van deze rechthoek min de oppervlakte van de drie halve rechthoeken , en . Er geldt:
Zet een rechthoek van cm bij cm om figuur b. De oppervlakte van de figuur is de oppervlakte van deze rechthoek min de oppervlakte van de drie halve rechthoeken , en . Er geldt:
In de applet zie je hoe de oppervlakte van een driehoek altijd de helft is van de oppervlakte van de rechthoek eromheen. Van deze rechthoek is de lengte gelijk aan de basis van de driehoek en de breedte gelijk aan de hoogte van de driehoek:
Zolang basis en hoogte niet veranderen, verandert ook de oppervlakte van de driehoek niet. Je kunt dus de vorm van de driehoek veranderen door evenwijdig aan de basis te verschuiven zonder de oppervlakte te veranderen. Dit heet het principe van Cavalieri.
Het principe van Cavalieri blijft ook gelden als één van de hoeken op de basis stomp wordt.
De hoogte is dan een lijnstuk buiten de driehoek: de (loodrechte) afstand van de top tot het verlengde van de basis .
Elke vierhoek kun je verdelen in twee driehoeken.
De oppervlakte van een vierhoek is daarom gelijk aan de som van de oppervlaktes van de twee driehoeken waarin je hem kunt verdelen. Bij bijzondere vierhoeken levert dit eenvoudige formules op voor het
berekenen van de oppervlakte.
Is een vierhoek een parallellogram, dan levert het verdelen twee gelijke driehoeken op. De oppervlakte van een parallellogram is daarom precies twee keer de oppervlakte van één van die driehoeken.
In de voorbeelden zie je ook hoe je de oppervlakte van enkele andere bijzondere vierhoeken zoals de vlieger en het trapezium berekent.
Bereken de oppervlakte van .
Bereken de oppervlakte van .
Bij moet je even goed kijken welke zijde je als basis kiest. Zijde kan niet, omdat de afstand van tot deze basis niet is gegeven. Kies zijde als basis, want dan is punt het tegenoverliggende hoekpunt. is dan de bekende (loodrechte) afstand tot (het verlengde) van de basis, dus de hoogte van de driehoek.
Werk met de applet in de Uitleg.
Maak een parallellogram met basis en een hoogte van . (Gebruik daarbij handig het rooster).
Als je de plaats van en hebt gekozen, is er dan nog maar één parallellogram mogelijk?
ja
nee
Zie de figuur bij b. Nee, je kunt lijnstuk nog onbeperkt in dezelfde richting verschuiven, zodat de hoogte niet verandert.
In welke twee gelijke driehoeken kun je je parallellogram verdelen?
In en .
Heeft elk parallellogram met een basis van en een hoogte van dezelfde oppervlakte?
ja
nee
Ja. Omdat de basis en de hoogte hetzelfde blijven, hebben beide driehoeken waarin je het kunt verdelen dezelfde oppervlakte en het parallellogram dus ook.
Bereken die oppervlakte met de formule voor de oppervlakte van een parallellogram. Controleer vervolgens met het rooster in de applet dat het antwoord correct is.
Onder de
Andere lengtematen leidt je hiervan af: cm m, mm m, etc.
Over eenheden en hun voorvoegsels gaat onderdeel 6 van Rekenen 1.
Onder de
Andere oppervlaktematen leidt je hiervan af: omdat cm m is cm
Van een rechthoek bereken je snel de oppervlakte door de lengte en de breedte te vermenigvuldigen.
Een halve rechthoek is de helft daarvan.
Elke veelhoek is ofwel te verdelen in rechthoeken en halve rechthoeken, ofwel te omlijsten door een rechthoek waarvan je dan kleinere rechthoeken en halve rechthoeken kunt
Je kunt daarmee ook
Als een figuur wordt vergroot met vergrotingsfactor dan wordt ook de omtrek keer zo groot, maar de oppervlakte wordt keer zo groot.
Bereken de oppervlakte van .
Bereken ook de oppervlakte van waarvan de lengtes van de zijden precies keer zo groot zijn dan die van .
Voor de oppervlakte van een driehoek geldt:
Van is de basis m en de hoogte .
De lengte van bereken je met de stelling van Pythagoras. Ga na, dat m.
Dus is: m
Van zijn alle lengtes van zijden keer zo groot.
Dus is . (Welke hoeken overeenkomstige hoeken zijn is voor de oppervlakte niet van belang.)
De basis van is (bijvoorbeeld) m.
De bijbehorende hoogte is dan m.
Dus is: m
Bekijk
Reken zelf de lengte van hoogte na.
Omdat is m.
In het voorbeeld zie je hoe je met die hoogte de oppervlakte van berekent.
Hoe kun je de omtrek van berekenen?
Bereken eerst m.
De omtrek van is dan m.
Hoe groot is de omtrek van ?
m.
is een driehoek waarvan alle zijden keer zo groot zijn dan die van .
Hoe groot zijn de omtrek en de oppervlakte van ?
m.
m
Bereken van deze driehoeken de oppervlakte en de omtrek.
en .
Bij bereken je eerst de hoogte en de zijde .
en .
De punten , , en zijn gegeven. Neem cm als roostereenheid.
Teken in een assenstelsel. Bereken de oppervlakte van deze driehoek met behulp van de oppervlakteformule.
Teken in een nieuw assenstelsel. Waarom kun je de oppervlakte van niet exact met behulp van de oppervlakteformule berekenen?
Zie bij de uitwerking van c.
Je kunt de oppervlakte
niet exact met behulp van de oppervlakteformule berekenen, omdat de basis en
hoogte nu niet op roosterlijnen en tussen roosterpunten staan. Je kunt de
afmetingen wel opmeten, maar dat is minder nauwkeurig.
Bereken op een andere manier de exacte oppervlakte van .
Zet eerst een vierkant om .
Meet nu de lengte van en meet de afstand van punt tot in millimeter nauwkeurig.
Bereken met die getallen de oppervlakte van . Rond af op één decimaal.
Neem als basis cm. De bijbehorende hoogte , de
afstand van tot , is ongeveer cm. De
hoogte van een driehoek is altijd de afstand van het hoekpunt tegenover de
basis (loodrecht) naar deze basis.
Bereken de oppervlakte en de omtrek van deze vlieger.
Vlieger bestaat uit vier rechthoekige driehoeken:
De oppervlakte van de vlieger is daarom eenheden.
Voor de omtrek moet je de lengtes van de vier zijden optellen.
De lengtes van en moet je nog berekenen.
Met de stelling van Pythagoras:
.
De omtrek is daarom ongeveer .
Bereken de oppervlakte en de omtrek van de vlieger en de ruit.
Je kunt de figuren eventueel ook opdelen in twee niet-rechthoekige driehoeken.
Voor de omtrek bereken je eerst de zijden:
van de vlieger zijn de twee langste zijden en de twee kortste zijden ;
van de ruit zijn alle zijden .
Bekijk de vlieger.
Laat zien waarom geldt:
Je kunt dit bijvoorbeeld uitleggen door er een rechthoek omheen te tekenen (zie figuur) en dan uit te leggen waarom de vlieger precies de halve oppervlakte van die rechthoek heeft.
Een andere manier is, om de oppervlaktes van de twee afzonderlijke driehoeken in en uit te drukken, deze bij elkaar op te tellen en de formule te vereenvoudigen.
Een vlieger heeft altijd (minstens) één symmetrieas. De bovenste twee rechthoekige driehoeken hebben dus dezelfde oppervlakte, aangezien beide naast de gedeelde zijde ook een zijde van hebben. Hetzelfde geldt voor de onderste twee rechthoekige driehoeken. De vlieger past twee keer in de rechthoek, dus de oppervlakte van de figuur is de helft van de rechthoek, dus .
Of laat het zien door bijvoorbeeld de vlieger via de verticale diagonaal (de symmetrieas) te verdelen in twee dezelfde driehoeken met basis en hoogte :
Bekijk vlieger en
Je ziet dat je iedere vlieger kunt opdelen in twee identieke driehoeken aan weerszijden van symmetrieas . In vlieger zijn dit en en in vlieger zijn dit en . Door het evenwijdig met de symmetrieas verschuiven van de toppen en in vlieger ontstaat vlieger met toppen en , met een stompe hoek op de symmetrieas. Aangezien de hoogte van de bijbehorende identieke driehoeken niet verandert, blijft de oppervlakte van de driehoeken gelijk. De formule voor de oppervlakte blijft dus ook gelijk. De formule geldt voor vlieger en voor pijlpuntvlieger .
Geldt deze formule voor de oppervlakte van een vlieger voor elke vlieger? Dus ook voor een ruit bijvoorbeeld?
ja
nee
Ja, zolang de diagonalen van de vierhoek maar loodrecht op elkaar staan is deze formule geldig.
Bereken de oppervlakte van het trapezium.
Het trapezium bestaat uit twee driehoeken met gelijke hoogte. Deze hoogtes zijn aangegeven met de lijnstukken en .
Bekijk het trapezium in het voorbeeld. Je kunt de oppervlakte van dit trapezium ook berekenen met de driehoeken die ontstaan door diagonaal te trekken. Laat zien dat je dan dezelfde oppervlakte krijgt.
Nu krijg je met
De driehoeken houden dezelfde waarden voor de basis en hoogte, dus de afzonderlijke en de totale oppervlakte veranderen niet.
Bekijk het trapezium. Als de lengte van de twee evenwijdige zijden en de afstand tussen die twee zijden is gegeven, kun je de oppervlakte van het trapezium berekenen.
Laat zien dat de oppervlakte van dit trapezium gelijk is aan .
Verdeel het trapezium in twee driehoeken door een diagonaal te trekken. Dan is
Bereken, met behulp van de bij a gevonden oppervlakteformule, de oppervlakte van het trapezium uit het voorbeeld.
m
Je vindt voor de oppervlakte m
Teken zelf een
Ja, de oppervlakteformule van a is ook nu geldig.
Ja, de oppervlakteformule van a is ook nu geldig, want de hoogte van de (nu stomphoekige) driehoeken verandert niet.
Kun je van dit trapezium de omtrek berekenen? Licht je antwoord toe.
Nee, je kunt de lengtes van en niet berekenen.
Er zijn ook andere trapezia te tekenen met dezelfde hoogte, en dezelfde lengtes van de twee evenwijdige zijden.
Bekijk het trapezium. Gegeven is: , en de oppervlakte is . Bereken de lengte van zijde .
Je moet oplossen: . Je vindt: .
Hier en op het werkblad zie je een A en een L op roosterpapier. Je mag er van uitgaan dat de hoekpunten van de letter A die geen roosterpunt zijn telkens precies midden tussen twee roosterpunten liggen. Let op: de roostereenheid is cm.
Bereken van zowel de A als de L de exacte oppervlakte in mm
letter A: mm
letter L: mm
Het is het handigst om eerst de oppervlakten van de figuren in roosterhokjes
te berekenen en deze daarna pas om te zetten naar mm
roosterhokjes mm
( is hierbij horizontaal opgedeeld in rechthoekige driehoeken).
Waarom kun je wel van de L, maar niet van de A de exacte omtrek bepalen?
De zijden van de L liggen op roosterlijnen en de hoekpunten zijn roosterpunten.
Bij de A is beide niet het geval.
De zijden van de L liggen op roosterlijnen en de hoekpunten zijn roosterpunten.
Bij de A is beide niet het geval.
Bereken de omtrek van de L in mm.
mm
De omtrek van de L is hokjes mm.
Deze figuren staan ook op het werkblad.
a
b
c
d
e
f
Bereken de oppervlakte van de figuren. Je mag ervan uitgaan dat de figuren d en e lijnsymmetrisch zijn.
Figuur a:
Figuur b:
Figuur c:
Figuur d:
Figuur e:
Figuur f:
Figuur a:
Figuur b:
Figuur c:
Figuur d:
Figuur e:
Figuur f:
a
b
c
d
e
f
In een assenstelsel zijn de punten , , en gegeven.
Bereken de oppervlakte van .
Zie de figuur bij de uitwerking van c.
Bereken de oppervlakte van .
Zie de figuur bij uitwerking c.
Bereken de oppervlakte van .
De lengtes van de zijden zijn niet exact bekend. Om de oppervlakte exact te kunnen berekenen, moet je een rechthoek om tekenen.
Bekijk de twee driehoeken.
Bereken van beide driehoeken de oppervlakte en de omtrek.
Bekijk de drie vierhoeken: een parallellogram, een pijlpuntvlieger en een trapezium.
Bereken de oppervlakte van deze vierhoeken.
Bekijk de figuur. De onderkant en de bovenkant lopen evenwijdig. De linker bovenhoek is een rechte hoek (). Alle maten zijn in centimeters.
Bereken de oppervlakte van deze staalplaat.
Je kunt de figuur verticaal verdelen in twee trapezia.
De oppervlakte is cm
Je kunt de figuur verticaal verdelen in twee trapezia.
De oppervlakte is cm
Je ziet hier een rechthoekige driehoek . De afmetingen van de zijden staan in de figuur.
Bereken de exacte lengte van lijnstuk met behulp van de oppervlakte van .
.
is de hoogte op basis .
Omdat de oppervlakte van
deze rechthoekige driehoek gelijk is aan , geldt ook:
. Links en rechts eerst en dan delen door
, dan is .
Een van de vele grote wiskundigen uit de Griekse Oudheid was Heron van Alexandrië. Hij leefde ongeveer van 10 na Christus tot 70 na Christus. Hij heeft een groot aantal formules bedacht, waaronder een formule om de oppervlakte van een driehoek te berekenen aan de hand van de lengtes van de drie zijden.
Deze formule staat ook wel bekend als de formule van Heron.
Stel dat een driehoek zijden , en heeft, dan luidt de formule:
Daarbij staat voor de helft van de omtrek van de driehoek.
Bekijk de formule van Heron.
Waarom geldt ?
staat voor de halve omtrek. De omtrek bereken je door , en bij elkaar op te tellen, ofwel: . De helft daarvan is . Dus
Gegeven is een rechthoekige driehoek met zijden van cm, cm en cm.
Bereken de oppervlakte van deze driehoek met de bekende formule met basis en hoogte.
De rechthoekszijden van deze driehoek zijn cm en cm lang. Die kun je meteen als basis en hoogte gebruiken. Er geldt dan:
Invullen geeft:
De rechthoekszijden van deze driehoek zijn cm en cm lang. Die kun je meteen als basis en hoogte gebruiken. Er geldt dan:
Invullen geeft:
Bereken de oppervlakte met de formule van Heron. Ga na dat je dezelfde uitkomst krijgt.
Dit klopt, want het is dezelfde uitkomst als bij b.
Bereken eerst met de formules die je bij a hebt gevonden. Je vindt dan: . Dus .
Bereken eerst de getallen , en .
Vul alles nu in in de formule van Heron:
Dit klopt, want het is dezelfde uitkomst als bij b.
Bereken de oppervlakte van een driehoek met zijden van cm, cm en cm. Rond af op twee decimalen.
Bereken eerst met de formules die je bij a hebt gevonden. Je vindt dan: . Dus .
Bereken eerst met de formules die je bij a hebt gevonden. Je vindt dan: . Dus .
Nu bereken je de getallen , en .
Vul alles nu in in de formule van Heron:
Het productiebedrijf SProces BV heeft een productiehal waarin zich een vierkant gebied bevindt. Daarop staan de vulmachines. Van dit vierkante gebied wordt een rechthoekig gedeelte gereserveerd voor de opslag van producten (links onder); de vloer hiervan wordt groen geverfd. De rest van de vloer is grijs. Zie tekening; de verhoudingen in de tekening zijn misschien niet juist.
Op de rand van het grijze gedeelte wordt (aan alle kanten) een zwarte lijn geverfd. De totale lengte van deze zwarte lijn is m. De breedte van de lijn wordt verwaarloosd.
De lengte en de breedte zijn overal hele meters.
De totale oppervlakte van het grijze gedeelte is m
De totale omtrek van het groene gedeelte is m.
Bereken de lengte van het rechthoekige groene gedeelte dat gereserveerd is voor de opslag van producten.
meter.
De totale lengte van de zwarte lijn is gelijk aan de omtrek van het complete, vierkante gebied.
De omtrek van een vierkant is keer de lengte van een zijde. De zijde van het vierkant is dus meter.
De oppervlakte van het totale vierkant is m
De oppervlakte van het grijze deel is m
De omtrek van het groene deel is m. De lengte () en breedte () zijn samen meter (de halve omtrek).
Dus: en .
Aangezien en allebei een geheel aantal meters zijn, is er maar één mogelijkheid: het groene deel is bij m, want (de oppervlakte) en meter (de halve omtrek).
De lange zijde van de rechthoek is dus meter.
Hier zie je drie figuren, een driehoek , een parallellogram en een trapezium met .
Bereken van elke figuur de omtrek en de oppervlakte.
en
en
en
:
en .
en
:
.
en
:
en .
en
Van een driehoek is de hoogte op gelijk aan cm en de oppervlakte is cm
Bereken de lengte van .
cm
Neem als basis, dan is de bijbehorende hoogte cm en geldt:
Dus cm.
De figuur bestaat uit twee driehoeken. De zijden aan de onder- en de bovenkant van de figuur lopen evenwijdig aan elkaar. De afstandslijnen staan loodrecht op elkaar.
Bereken de oppervlakte van de totale figuur.
dm