de wortel-n-wet voor het verband tussen de standaardafwijking van steekproefgemiddelden en de populatiestandaardafwijking;
werken met betrouwbaarheidsintervallen rondom de schatting van het populatiegemiddelde.
de standaardafwijking van een frequentieverdeling uitrekenen en interpreteren;
een percentage onder een normale verdeling berekenen;
het gemiddelde of de standaardafwijking van een normale verdeling berekenen.
De Robinia is een boom die in het najaar peulvruchten heeft van zo'n cm tot cm lengte. De lengtes van deze peulen is normaal verdeeld en heeft een gemiddelde van cm met een standaardafwijking van cm.
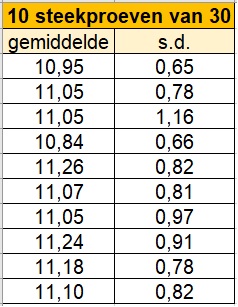
Je ziet hier gemiddelde lengtes en de standaardafwijkingen van steekproeven van uit de normaal verdeelde populatie peulen.
Kijk naar de resultaten en van de eerste steekproef van . Kun je uit alleen deze gegevens het gemiddelde van de populatie schatten?
Eigenlijk niet, toevallig levert deze steekproef een iets te laag gemiddelde op.
Bereken het gemiddelde van de steekproefgemiddelden.
Zit dit dicht bij het populatiegemiddelde?
cm en dat zit dus heel dicht bij het populatiegemiddelde.
De steekproefgemiddelden vormen een steekproevenverdeling.
Wiskundigen hebben aangetoond dat een steekproevenverdeling altijd een normale verdeling is met standaardafwijking als de grootte van elke steekproef is.
Hoe groot is de standaardafwijking van de steekproevenverdeling?
Is dit ongeveer gelijk aan ?
en .
Het klopt ongeveer?
Leg uit waarom % van de steekproefgemiddelden tussen en zou moeten liggen.
Omdat de steekproefgemiddelden normaal zijn verdeeld, kun je de vuistregels voor een normale verdeling gebruiken.
Je wilt op grond van de steekproeven een schatting maken van het populatiegemiddelde. Wat zou je doorgeven?
Bijvoorbeeld dat het populatiegemiddelde met een waarschijnlijkheid van % tussen en ligt.

De Robinia is een boom die in het najaar peulvruchten heeft van zo'n cm tot cm lengte. De lengtes van de peulen in een bepaald gebied is normaal verdeeld.
Het populatiegemiddelde wordt bepaald door in een steekproef van peulen het gemiddelde te berekenen. Het probleem daarbij is dat het gemiddelde in een steekproef toevallig kan afwijken van het werkelijke gemiddelde, zelfs als de steekproef behoorlijk groot is. Je zou dus meerdere of hele grote steekproeven moeten doen. Vaak is dat in de praktijk te veel werk (en dus te duur).
Je ziet hier gemiddelde lengtes en de standaardafwijkingen van steekproeven van uit de normaal verdeelde populatie peulen.
De steekproefgemiddelden vormen een steekproevenverdeling .
Wiskundigen hebben aangetoond dat een steekproevenverdeling altijd een normale verdeling is met standaardafwijking als de grootte van elke steekproef is en de populatiestandaarddeviatie is. Dit heet de wortel-n-wet.
Ga zelf na dat in de steekproevenverdeling van de gemiddelden de standaardafwijking is.
Stel nu dat je alleen de eerste steekproef van peulen zou hebben gedaan.
Op grond van het gemiddelde cm kun je natuurlijk niet zeker weten dat het populatiegemiddelde ook is. Maar omdat je weet dat steekproefgemiddelden normaal zijn verdeeld, kun je op grond van de vuistregels van de normale verdeling zeggen:
% van de gemiddelden ligt tussen en .
En op grond hiervan schat je dat met een betrouwbaarheid van %.
Je noemt het % betrouwbaarheidsinterval van .
Bekijk het schatten van het populatiegemiddelde van de lengtes van peulen van de Robinia in de Uitleg. Je ziet de resultaten van steekproeven van peulen.
De gemiddelden vormen een steekproevenverdeling.
Bereken zelf het gemiddelde en de standaardafwijking van deze steekproevenverdeling.
en .
Laat zien dat voor de standaarddeviatie van de steekproevenverdeling van de gemiddelden inderdaad de wortel-n-wet geldt.
Het gemiddelde van de standaardafwijkingen is cm. (Zelf narekenen!).
en dat is ongeveer gelijk aan .
Je weet nu dat de steekproevenverdeling van de gemiddelden een normale verdeling is met een bij a berekend gemiddelde en standaarddeviatie. Bereken met de standaardnormale tabel de waarden van waarvoor geldt: .
geeft:
en dus .
Dus is .
Schrijf het % betrouwbaarheidsinterval op dat hierbij hoort.
, dus cm.
In de praktijk gebruik je maar één steekproef. Ga uit van de eerste steekproef. Je neemt dan aan dat hier een steekproevenverdeling bij hoort met en .
Bepaal het % betrouwbaarheidsinterval dat dan bij een schatting van het populatiegemiddelde hoort op dezelfde manier als bij d.
, dus cm.
In de Uitleg wordt een vuistregel gebruikt om het betrouwbaarheidsinterval op te schrijven. In de voorgaande opgave wordt dit met behulp van -waarden gedaan.
Wat is het voordeel van het werken met -waarden?
Laat zien dat % van de -waarden tussen en ligt.
Dat is nauwkeuriger.
geeft en dit geeft .
Tussen welke twee waarden ligt % van de -waarden?
Welk % betrouwbaarheidsinterval voor de steekproef met krijg je?
geeft en dit geeft .
Het % betrouwbaarheidsinterval is , dus cm.
Een % betrouwbaarheidsinterval lijkt beter dan een % betrouwbaarheidsinterval.
Wat is het nadeel ervan?
Het populatiegemiddelde wordt minder nauwkeurig geschat.
In de Uitleg wordt de gemiddelde lengte van een populatie peulen van de Robinia geschat.
Waarom liggen in dit geval zowel het populatiegemiddelde als de populatiestandaarddeviatie niet vast?
Al die peulen hebben verschillende lengtes die ook echt normaal verdeeld zijn.
Welke aanname moet je dan doen om een betrouwbaarheidsinterval te kunnen vaststellen?
Dat de standaardafwijking van de meting ongeveer gelijk is aan de populatiestandaarddeviatie.
Bij het meten van de pH-waarde van een vloeistof in een bepaald vat heb je te maken met een vooraf bekende meetnauwkeurigheid.
Waarom zal nu de standaardafwijking van bijvoorbeeld metingen vooraf bekend zijn?
De spreiding van de uitkomsten van de metingen wordt nu uitsluitend bepaald door de meetnauwkeurigheid. En dus zal ook de standaardafwijking vooraf kunnen worden berekend uit de meetnauwkeurigheid. Hierover meer in
Bij statistisch onderzoek is vaak het
Als er veel steekproeven worden genomen zal de
waarin de grootte van de steekproeven en de populatiestandaarddeviatie is.
Omdat de steekproefgemiddelden normaal verdeeld zijn, kunnen met behulp van de -tabel grenzen worden bepaald waarbinnen een bepaald percentage van de waarden ligt. Daarmee kun je het gebied waarin het populatiegemiddelde ligt berekenen.
Dit gebied heet het
De grenswaarden van het %-betrouwbaarheidsinterval bereken je zo
en .
De grenswaarden van het %-betrouwbaarheidsinterval bereken je zo
en .
De conclusie is dan:
Met een betrouwbaarheid van of % ligt het gemiddelde van de populatie tussen de
In een ziekenhuis wordt onderzoek gedaan naar het gemiddeld geboortegewicht van alle baby's die het afgelopen jaar zijn geboren. Er wordt een steekproef genomen van baby's.
Het gemiddelde gewicht van de baby's in de steekproef is het steekproefgemiddelde kg.
De standaardafwijking van het gewicht in de steekproef is kg.
Tussen welke twee grenzen ligt met % betrouwbaarheid het gemiddelde geboortegewicht van alle baby's in dit ziekenhuis?
De gemiddelden (hier van geboortegewichten) van veel steekproeven zijn normaal verdeeld. Als schatting voor het gemiddelde van deze steekproevenverdeling wordt nu genomen:
kg.
De standaardafwijking van deze gemiddelden is
.
Met % betrouwbaarheid ligt het gemiddeld geboortegewicht van alle baby's die het afgelopen jaar zijn geboren tussen en , dus tussen en kg. Dit is het %-betrouwbaarheidsinterval van het populatiegemiddelde.
Bekijk
Bereken de standaardafwijking van de steekproevenverdeling als er steeds steekproeven van baby's zouden zijn onderzocht. Neem aan dat de standaardafwijking in de steekproef niet veranderd zou zijn.
kg.
Hoe groot is in de uitleg het verschil tussen de bovengrens en de ondergrens van het gebied waarin het gemiddelde gewicht van alle baby's ligt?
kg.
kg of kg.
Soms wil een onderzoeker een kleiner betrouwbaarheidsinterval voor het gemiddelde in een populatie.
Wat kan een onderzoeker aan de steekproef veranderen om daarvoor te zorgen? Licht je antwoord toe.
De steekproefomvang groter maken. Dan wordt de standaardafwijking van de steekproevenverdeling kleiner, dus het gebied ook.
Wordt het gebied groter als een betrouwbaarheid % wordt genomen in plaats van %?
Ja, want om de betrouwbaarheid groter te maken, moet het gebied groter worden.
Een fabriek voor voedingsmiddelen neemt elke dag monsters van een product. Daarvan meet men het aantal bacteriën per cl. Daarna berekent men het daggemiddelde en de dagstandaardafwijking van deze monsters. De dagstandaardafwijking is steeds bacteriën per cL.
Dit wordt dagen herhaald. Er zijn dan daggemiddelden. Van de daggemiddelden is deze steekproevenverdeling gemaakt.
Bepaal het %-betrouwbaarheidsinterval van het gemiddeld aantal bacteriën per cL in het product met behulp van de figuur.
Wat is de betekenis van dit interval?
Als zowel het gemiddelde als de standaardafwijking van het aantal bacteriën per cl in de dagproductie kleiner zijn dan respectievelijk en , heeft dat gevolgen voor het %-betrouwbaarheidsinterval.
Beredeneer wat deze gevolgen zijn.
Neem aan dat de populatiestandaardafwijking is bacteriën per cL.
De figuur is de steekproevenverdeling.
De standaardafwijking daarvan is .
Het %-betrouwbaarheidsinterval is:
.
Het populatiegemiddelde ligt dus tussen en bacteriën per cL.
De betekenis is: Van de daggemiddelden, zijn er minstens met een gemiddelde tussen en bacteriën per cl.
Als het gemiddelde afneemt, schuift het interval naar links.
Als de standaardafwijking kleiner wordt, wordt het interval smaller.
Bekijk
Komt de standaardafwijking overeen met de figuur?
Ja, want de figuur is de steekproevenverdeling en deze is dus normaal verdeeld. De standaardafwijking van een normale verdeling is af te lezen bij het buigpunt.
Wat verandert er aan het betrouwbaarheidsinterval als het gemiddelde toeneemt?
Dan schuift het naar rechts.
Wat gebeurt er met het betrouwbaarheidsinterval als de standaardafwijking groter wordt?
Dan wordt het breder.
Wat gebeurt er met de kleinste waarde van het betrouwbaarheidsinterval als de standaardafwijking groter wordt?
Die wordt kleiner. (De grootste waarde wordt groter.)
Een ziekenhuis heeft een nieuw computersysteem aangeschaft voor het plannen van onderzoeken voor patiënten. Vóór de aanschaf van het computersysteem was de doorlooptijd (de tijd tussen het eerste en het laatste onderzoek) gemiddeld dagen. De standaardafwijking was erg klein.
Uit een representatieve steekproef van patiënten blijkt dat het dat na de aanschaf van het computersysteem de gemiddelde doorlooptijd is gedaald tot dagen. De standaardafwijking van de doorlooptijd in de steekproef blijkt dagen te zijn.
Wat is het %-betrouwbaarheidsinterval van de gemiddelde doorlooptijd van de patiënten na invoering?
Neem nu aan dat de populatiestandaarddeviatie ook dagen is.
Dus het %-betrouwbaarheidsinterval ligt tussen en dagen.
Kan het ziekenhuis met % zekerheid zeggen dat de gemiddelde doorlooptijd is gedaald? Licht je antwoord toe.
Ja, want het % betrouwbaarheidsinterval ligt helemaal onder dagen (met de zeer kleine standaardafwijking).
Enkele maanden later herhaalt het ziekenhuis het onderzoek. De standaardafwijking van de steekproef blijkt nu dagen te zijn. Kan het ziekenhuis nu met % betrouwbaarheid zeggen dat het computersysteem het nu niet goed meer doet? Licht je antwoord toe.
Dus het %-betrouwbaarheidsinterval ligt tussen en dagen.
Het gemiddelde van de vorige steekproef was dagen. Dat ligt in het %-betrouwbaarheidsinterval.
Met % betrouwbaarheid kun je zeggen dat het computersysteem het nog steeds goed doet. Dus: Nee.
Een machine vult medicijnverpakkingen met poeder. Het gewenste vulgewicht is mg. De fabrikant bewaakt het vulgewicht. Daarom onderzoekt de kwaliteitsafdeling deze verpakkingen. Het is bekend dat door de nauwkeurigheid van de vulmachine de standaardafwijking van het vulgewicht mg is.
De kwaliteitsafdeling wil het vulgewicht met een nauwkeurigheid van % van het gewenste vulgewicht bepalen. Daarmee bedoelt hij dat de afwijking van het gewenste vulgewicht maximaal % ervan mag zijn. Hoe groot moet de steekproefomvang zijn om dit met een %-betrouwbaarheid te kunnen doen?
Voor de steekproefomvang geldt de formule .
Gegeven is mg.
De afwijking van het gewicht mag maximaal % van het gewenste gewicht zijn. Dat is mg.
Bij een betrouwbaarheid van % moet dus , zodat mg.
Dit betekent:
Oplossen geeft:
De steekproefomvang moet dus minstens zijn.
Bekijk
Los de vergelijking op.
geeft , zodat .
Als de kwaliteitsafdeling met een nauwkeurigheid van % het gewenste vulgewicht wil bepalen, hoe groot moet dan de steekproefomvang zijn?
Dan geldt: en dus .
Dit geeft .
Dus de steekproefomvang moet dan minstens zijn.
Als de nauwkeurigheid % zou zijn en de populatiestandaardafwijking zou verdubbelen, hoe groot zou dan de steekproefomvang moeten zijn?
geeft .
De steekproefomvang moet dan zijn.
De vuilnisdienst van een stad wil weten hoeveel huisvuil een gezin uit deze stad tweewekelijks buitenzet. Er wordt een aselecte steekproef genomen van gezinnen. Het gemiddelde gewicht huisvuil dat door deze gezinnen verbruikt werd was kg, met een standaardafwijking van kg.
Bereken het % betrouwbaarheidsinterval van de hoeveelheid huisvuil (in kg) dat per gezin in de hele stad wordt opgehaald.
kg
kg
% betrouwbaarheidsinterval tussenen , dus tussen en kg.
kg
kg
% betrouwbaarheidsinterval tussenen , dus tussen en kg.
Een vulmachine vult flesjes water. Een aselecte steekproef van flesjes geeft een gemiddelde inhoud van cL. De standaardafwijking is .
Bereken het % betrouwbaarheidsinterval.
Foutmarge:
% betrouwbaarheidsinterval: , dus .
Josephine beweert dat ongeveer % van de flesjes minder dan cL bevat.
Rachid beweert dat ongeveer % van de flesjes minder dan cL bevat.
Wie heeft gelijk?
Het % betrouwbaarheidsinterval is , dus ongeveer % van de flesjes valt daar buiten, aan beide zijden van het betrouwbaarheidsinterval evenveel. Dus ongeveer % van de flesjes bevat minder dan cL.
Een bedrijf maakt en verkoopt light producten. Ze beweert dat haar producten slechts calorieën per pakje bevatten . De Consumentenbond controleert dit met een aselecte steekproef van pakjes. Ze vinden gemiddeld calorieën. De standaardafwijking van deze steekproef is calorieën.
De bewering van het bedrijf lijkt niet te kloppen. Onderzoek of de Consumentenbond mag zeggen: met % betrouwbaarheid zit er meer dan calorieën in het lightproduct.
en , zodat .
Het % betrouwbaarheidsinterval is , dus .
valt niet in betrouwbaarheidsinterval. Dus de uitspraak de Consumentenbond mag dit zeggen.
Wat moet het bedrijf aanpassen aan het aantal calorieën zodat de uitspraak van de Consumentenbond niet klopt?
Het bedrijf kan het aantal calorieën per pakje verlagen, bijvoorbeeld met calorieën per pakje.
en , zodat .
Het % betrouwbaarheidsinterval wordt , dus .
valt nu wel binnen het betrouwbaarheidsinterval.
Bij een statistisch onderzoek wordt het populatiegemiddelde geschat. De standaardafwijking van de steekproevenverdeling is .
Hoe groot zijn de grenzen van het % betrouwbaarheidsinterval van het populatiegemiddelde?
Het % betrouwbaarheidsinterval is begrensd door en .
Hoe groot zijn de grenzen van het % betrouwbaarheidsinterval van het populatiegemiddelde?
Het % betrouwbaarheidsinterval is begrensd door en .
Een laborant analyseert de concentratie van een actieve stof in een geneesmiddel. De standaardafwijking van deze concentratie is bekend, deze is . De laborant doet drie metingen met als resultaat in g/L: , en .
Bereken gemiddelde en standaardafwijking van deze drie metingen. Rond je antwoord af op vier decimalen.
en .
Bepaal het % betrouwbaarheidsinterval voor de waarde van de gemiddelde concentratie van de actieve stof.
g/L.
Het % betrouwbaarheidsinterval is en , dus tussen en .
Hoeveel metingen moet de laborant minstens doen om de breedte van het % betrouwbaarheidsinterval kleiner dan te krijgen?
De breedte van het % betrouwbaarheidsinterval is .
Dit geeft .
De laborant moet minstens metingen doen.
Wanneer een laborant dezelfde meting een aantal keren met hetzelfde apparaat herhaalt, dan krijgt hij een serie waarden die meestal iets van elkaar verschillen. De standaarddeviatie is een maat voor de precisie van zijn metingen. Vaak wordt echter de standaarddeviatie gedeeld door het gemiddelde en in procenten uitgedrukt. Je krijgt dan de zogenaamde
variatiecoëfficiënt
Hier zie je hoe door metingen de pH-waarden in drie vloeistoftanks is gemeten.

Door de gebruikte meetmethode wijken de resultaten maximaal % af van de werkelijke waarde. De variatiecoëfficiënt is dus .
Je kunt hiermee voor elke tank een % betrouwbaarheidsinterval opstellen voor de geschatte pH-waarde.
Bekijk de gegevens van de eerste vloeistoftank in
Bereken de gemiddelde pH-waarde in deze tank.
.
Omdat de variatiecoëfficiënt bekend is, kun je met behulp van dit gemiddelde de standaardafwijking berekenen.
Laat zien hoe.
geeft , dus .
Je gebruikt de gegevens om de werkelijke pH-waarde te schatten.
Geef het bijbehorende % betrouwbaarheidsinterval.
Je gebruikt de gevonden waarden voor gemiddelde en standaardafwijking als schatting voor de pH-waarde.
Ondergrens .
Bovengrens .
Dus het % betrouwbaarheidsinterval is .
Bekijk de metingen van de pH-waarden in de andere twee tanks.
Stel ook voor die twee tanks het % betrouwbaarheidsinterval voor de schatting van de pH-waarde op.
Tank 2: en , dus .
Dus het % betrouwbaarheidsinterval is .
Tank 3: en , dus .
Dus het % betrouwbaarheidsinterval is .
Wijkt de pH-waarde van tank 2 duidelijk af van de andere twee pH-waarden?
Ja want het % betrouwbaarheidsinterval van tank 3 overlapt de andere twee niet.
In een steekproef van lampen is de gemiddelde levensduur van de lampen van de straatverlichting in een gemeente uur met een standaardafwijking van uur.
Bereken het % betrouwbaarheidsinterval van de schatting van het populatiegemiddelde.
.
De foutmarge voor % betrouwbaarheidsinterval is .
Het % betrouwbaarheidsinterval is ofwel .
De gemeente wil alle lampen vervangen als naar schatting % defect is. Na hoeveel uur gaat de gemeente met de vervanging van lampen beginnen?
Na circa uur.
Bij de ondergrens van het % betrouwbaarheidsinterval is ongeveer % van de lampen naar schatting kapot en gaat de lampen vervangen. En dat is na circa uur.
Bij een steekproef onder pasgeboren baby's is de lengte (in cm) gemeten. De gemiddelde lengte is cm en cm.
Bereken het % betrouwbaarheidsinterval.
.
De foutmarge voor % betrouwbaarheidsinterval is
Het % betrouwbaarheidsinterval is ofwel .
Onder de metingen zit een meetfout. Een van de baby's is geen maar cm. Dit heeft gevolgen voor het gemiddelde en voor . Nu is
Bereken het % betrouwbaarheidsinterval opnieuw.
Het gemiddelde wordt nu .
.
De foutmarge voor % betrouwbaarheidsinterval is
Het % betrouwbaarheidsinterval is ofwel .
Leg uit waarom een meetfout van één waarde in een kleine steekproef grotere gevolgen heeft dan een meetfout in een grote steekproef voor het betrouwbaarheidsinterval.
Het gemiddelde en de steekproefstandaarddeviatie veranderen nauwelijks in een grote steekproef bij een meetfout van één waarde.

Een applet van een groot aantal steekproeven (steekproefgrootte in te stellen) uit een populatie waarvan het populatiegemiddelde is in te stellen. Het doel is om te laten zien dat die steekproefgemiddelden normaal verdeeld liggen. Zo kun je een
Simulatie steekproeven om een populatiegemiddelde te schatten
Dit practicum is ontwikkeld door Piet van Blokland en Carel van de Giessen, zie www.vusoft.eu
Het trekken van aselecte steekproeven uit een populatie is ook te bekijken via het practicum: