het verband tussen twee statistische variabelen in beeld brengen als spreidingsdiagram;
de correlatiecoëfficiënt gebruiken om de sterkte van het (statistisch) verband tussen twee variabelen te berekenen;
het verband tussen twee statistische variabelen beschrijven met behulp van een regressielijn.
gemiddelde en standaardafwijking van een dataset bepalen (ook met behulp van Excel);
werken met grafieken in Excel.
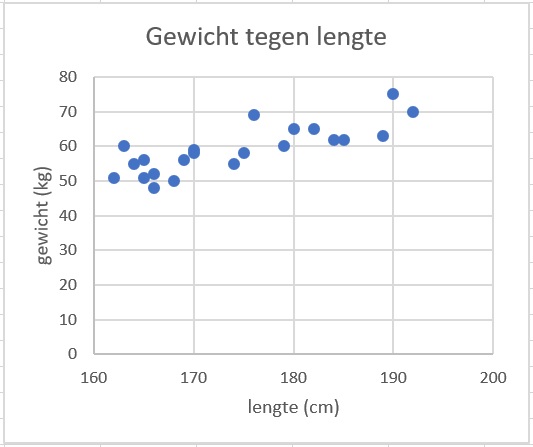
Om te onderzoeken of er een verband bestaat tussen lengte en gewicht bij mensen van 15 tot 17 jaar oud heb je gegevens nodig. Op het werkblad LengteGewicht22Studenten.xls vind je de gegevens van een groep van studenten. Hiernaast is een spreidingsdiagram van die gegevens getekend.
Welke drie gegevens zijn er verzameld?
Het geslacht, de lengte in cm en het gewicht in kg.
Welke afspraken moet je maken bij het verzamelen van deze gegevens? Beschrijf er een paar. (Denk om de manier van meten!)
Bijvoorbeeld recht tegen de muur staan, geen schoenen aan, hoofd recht vooruit, plankje op hoofd loodrecht op de muur, etc.
Bekijk het spreidingsdiagram. Trek je op grond van de gegevens op het werkblad de conclusie dat er zo'n verband bestaat? En is dat dan uitsluitend een statistisch verband of is het ook een oorzakelijk verband, m.a.w. wordt een groter gewicht veroorzaakt door een grotere lengte?
Je lijkt te kunnen zeggen dat een langer iemand ook zwaarder is. Dat is vooral een statistisch verband, een groter gewicht wordt beslist niet alleen veroorzaakt door een grotere lengte, de leefstijl speelt daar ook een grote rol bij.

Je wilt onderzoeken of er een verband bestaat tussen lengte en gewicht bij mensen van 15 tot 17 jaar oud. Op het werkblad LengteGewicht22Studenten.xls vind je de gegevens van een steekproef van studenten. Hiernaast is een spreidingsdiagram van die gegevens getekend.
Is er binnen deze groep studenten sprake van een verband tussen lengte en gewicht?
Als je de figuur bekijkt, zie je dat bij grotere lengtes vaak ook grotere gewichten horen.
Er lijkt dus een zeker verband te zijn.
Maar de getekende punten liggen zeker niet op één lijn, dus hoe sterk is het verband?
De sterkte van het verband wordt uitgedrukt in de correlatiecoëfficiënt , waarin de lengte in cm en het gewicht in kg is. is een maat voor de gemiddelde van de afstanden van de punten tot het punt :
Hierin is het aantal metingen van combinaties .
Met behulp van Excel kun je een correlatiecoëfficiënt berekenen.
Hij kan alleen waarden aannemen vanaf tot en met . Hoe dichter bij of , hoe beter de correlatie.
Bij is er geen enkele correlatie en dus geen verband tussen en .
Gebruik het werkblad LengteGewicht22Studenten.xls in Uitleg.
Maak zelf zo'n spreidingsdiagram.
Haal het bestaande diagram eerst weg.
Kies bij Invoegen voor
Voeg aslabels toe.
Hoe zie je in het spreidingsdiagram dat er een zeker verband tussen en bestaat?
Als toeneemt, neemt in het algemeen ook toe.
Bereken de correlatiecoëfficiënt in twee decimalen nauwkeurig.
Bereken eerst , , en .
Maak in Excel kolommen voor (b.v. E-kolom), (b.v. F-kolom) en voor (b.v. G-kolom).
Tel deze laatste kolom op, daar komt uit.
Laat Excel met behulp hiervan berekenen: .
Je hebt de waarde van berekend. Maar hoe weet je nu of deze correlatie genoeg is om vast te stellen dat er een verband is?
Daarvoor gebruik je deze r-tabel. Als jou waarde van groter is dan die in de tabel, dan is het verband aangetoond, afhankelijk van de gewenste betrouwbaarheid.
Kun je vaststellen dat er een duidelijk verband is tussen lengte en gewicht van deze jongeren met een betrouwbaarheid van %?
Je moet in de tabel kijken bij en %.
Daarbij hoort een -waarde: .
Omdat bestaat er inderdaad zo'n verband met een betrouwbaarheid van %.
Je hebt in de voorgaande opgave een verband aangetoond tussen lengte en gewicht bij mensen van 15 tot 17 jaar oud.
Daarbij gebruikte je een steekproef van studenten.
Geef commentaar op deze steekproef.
De steekproef is erg klein, eigenlijk te klein om iets over de groep mensen van 15 tot 17 jaar oud te kunnen zeggen. Bovendien zijn het studenten, dat is al een speciale groep. Verder is onduidelijk hoe de groep is samengesteld.
Stel je voor dat je met een aselecte steekproef te maken hebt. En neem ook aan dat de groep representatief is voor studenten van 15 tot 17 jaar oud. Er is een duidelijk verband gevonden.
Is er nu sprake van een oorzakelijk verband, dus is de lengte oorzaak van het gewicht?
Of is er alleen een statistisch verband? Licht het antwoord toe.
Je kunt zeker niet zeggen dat de lengte de oorzaak is van het gewicht. Het is wel één van de oorzaken, maar de leefstijl is waarschijnlijk een nog veel grotere oorzaak. Het verband is zeker statistisch en deels oorzakelijk.
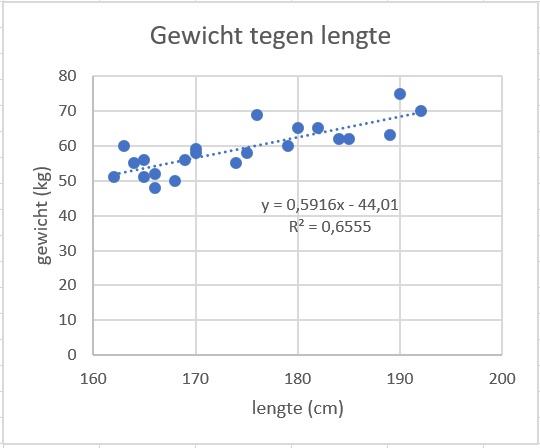
Je wilt onderzoeken of er een verband bestaat tussen lengte en gewicht bij mensen van 15 tot 17 jaar oud. Op het werkblad LengteGewicht22Studenten.xls vind je de gegevens van een steekproef van studenten. Hiernaast is een spreidingsdiagram van die gegevens getekend.
Er is binnen deze groep studenten sprake van een verband tussen lengte en gewicht, maar hoe beschrijf je dit verband?
Je ziet in de figuur hoe Excel automatisch het kwadraat van de correlatiecoëfficiënt berekend en een best passende lijn door de puntenwolk trekt. Deze lijn heet de regressielijn. En heet de determinatiecoëfficiënt.
De regressielijn gaat door en de hellingwaarde (richtingscoëfficiënt) is:
Daarmee vind je de formule voor de regressielijn: .
De determinatiecoëfficiënt geeft aan dat ongeveer % van het gewicht wordt veroorzaakt door de lengte.
Je ziet in Uitleg hoe Excel een lijn door de puntenwolk trekt en de bijbehorende formule berekent.
Doe dit zelf met het werkblad LengteGewicht22Studenten.xls.
Als het goed is heb je het spreidingsdiagram (de puntenwolk) nog; maak hem anders opnieuw.
Voeg nu een
Je ziet in de uitleg hoe je zelf de formule voor de trendlijn kunt berekenen.
Voer die berekening uit.
Je hebt al eerder gevonden: en .
De formule wordt: .
Vul daarin en in: geeft .
Dus de formule wordt .
Je kunt nu met behulp van de gevonden regressielijn (trendlijn) voorspellingen doen.
Hoe zwaar zou iemand van m volgens de regressielijn moeten zijn?
kg.
In een
Als dan is er een perfecte positieve correlatie tussen en . De punten van de puntenwolk liggen dan precies op een stijgende lijn.
Als dan is er geen enkele correlatie tussen en .
Als dan is er een perfecte negatieve correlatie tussen en . De punten van de puntenwolk liggen dan precies op een dalende lijn.
De correlatie tussen en wordt beter naarmate dichter bij of ligt.
Gebruik de r-tabel.
Als bij positieve correlatie dan is het verband aangetoond, afhankelijk van de gewenste betrouwbaarheid.
Als bij negatieve correlatie dan is het verband aangetoond, afhankelijk van de gewenste betrouwbaarheid.
In Excel wordt vaak de determinatiecoëfficiënt gegeven.
Een verband waarbij de toename (of afname) van de éne variabele een gevolg is van een toename (of afname) van de andere heet een
Als de correlatie tussen de variabelen en groot genoeg is, kun je een formule
van de vorm opstellen die het verband tussen en weergeeft.
Deze formule heeft als grafiek een rechte lijn, de
Deze richtingscoëfficiënt heet wel de
De makers van een veelgebruikte weerapp en de uitbaters van een dierentuin doen een onderzoek naar een eventueel verband tussen de kans op regen die de weerapp voor een zaterdag voorspelt en het aantal dierentuinbezoekers op die zaterdag.
Na een aantal weken hebben ze de volgende gegevens verzameld.

Maak hiervan een spreidingsdiagram en stel een formule op voor de regressielijn.
Hoe groot is de correlatiecoëfficiënt van de kans op regen en het aantal bezoekers in deze steekproef?
Laat Excel de determinatiecoëfficiënt berekenen en de formule voor de trendlijn opstellen.
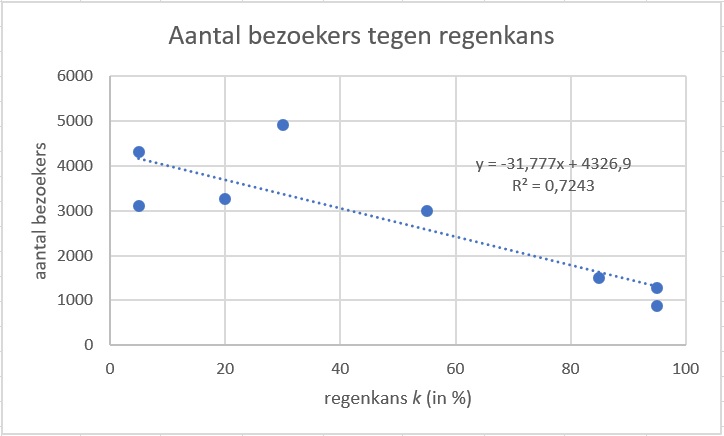
De regressielijn is . (Afronden op gehele bezoekers lijkt logisch.)
Je vindt: .
Gebruik de gegevens in
Maak zelf het spreidingsdiagram en laat Excel de formule van de regressielijn opstellen en de determinatiecoëfficiënt berekenen.
Zet eerst de gegevens in Excel.
Kies bij Invoegen voor
Voeg aslabels en de trendlijn toe.
Stel bij
Bereken de correlatiecoëfficënt.
Wat betekent het dat de correlatiecoëfficiënt een negatief getal is?
Hoe hoger de waarden van de éne variabele des te lager die van de andere.
Je kunt de formule van de regressielijn ook berekenen met behulp van de correlatiecoëfficiënt en de gemiddelden en de standaarddeviaties. Laat zien hoe.
.
Dan is en deze lijn gaat door .
Dit punt invullen geeft .
Tenslotte nog afronden op gehele bezoekers.
Is er met een betrouwbaarheid van % een verband tussen en ?
Gebruik de r-tabel: en . Nu is dus de negatieve correlatie is aangetoond met een betrouwbaarheid van %.
Voorspel op basis van de regressielijn het aantal bezoekers bij een regenkans van %.
bezoekers.
Bekijk
Behalve de regenkans wordt ook het voorspelde aantal uren zon bijgehouden. Bij de dierentuin zit ook een vennetje waarin kinderen kunnen zwemmen en dit aantal kinderen heeft men bijgehouden:
| 0,7 | 7,6 | 2,3 | 1,1 | 2,4 | 4,9 | 8,1 | 3,6 | |
| 6 | 802 | 121 | 6 | 48 | 123 | 964 | 32 |
Bereken de correlatiecoëfficiënt.
Maak een aparte lijst/kolom voor zonuren en aantal zwemmende kinderen en zorg dat de correlatiecoëfficiënt wordt berekend.
Is dit een betekenisvol correlatieonderzoek? Zegt de correlatiecoëfficiënt in dit geval ook echt iets over een mogelijk verband tussen het voorspelde aantal uren zon en het aantal kinderen dat gaat zwemmen?
Een belangrijk argument tegen de zinvolle betekenis van dit onderzoek is dat je niet zeker weet dat de voorspelde zonuren de doorslag geven om te zwemmen en niet de ervaren weersomstandigheden op het moment zelf. Daar zou eerst onderzoek naar moeten worden gedaan.
Daarnaast betreft het hier een wel erg kleine steekproef. Dat betekent dat de betrouwbaarheid van de uitspraken die je op basis van deze correlatiecoëfficiënt kunt doen erg klein is.
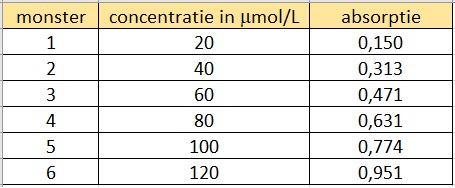
Om bij iemand bloedarmoede aan te tonen wordt vooraf spectrofotometrisch het ijzergehalte in serum bepaald.
Van een kalibratielijn worden de absorptiewaarden gemeten, zie tabel.
Maak hiervan een spreidingsdiagram en bereken de bijbehorende correlatiecoëfficiënt.
Stel een formule op voor de regressielijn van de absorptiewaarde afhankelijk van de concentratie in µmol/L en bepaal met behulp daarvan het ijzergehalte van iemand waarbij een absorptiewaarde van wordt gemeten.
Gebruik Excel en je vindt dit.
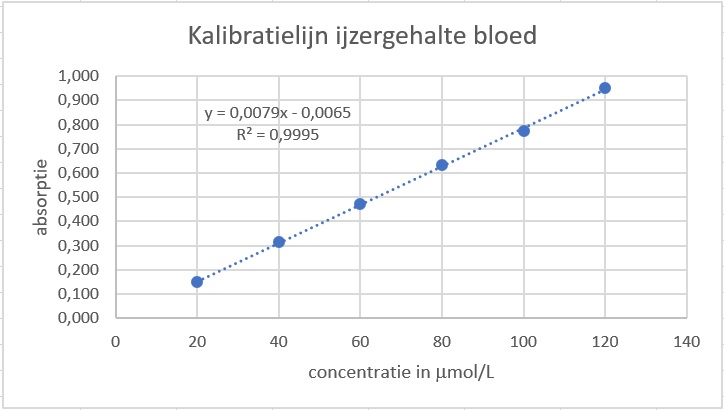
De correlatiecoëfficiënt is daarom en er is een vrijwel perfecte positieve correlatie.
Het verband tussen en is: .
Als bij iemand wordt gemeten, dan is
.
Dit geeft µmol/L.
In
Voer zelf de berekening van de correlatiecoëfficiënt en de formule voor de regressielijn uit.
Gebruik Excel, als het goed is weet je hoe dit gaat.
Laat zien dat als het ijzergehalte µmol/L is.
geeft en .
Waarom vind je hier een die vrijwel is?
Van vrouwen zijn de lichaamsmaten opgemeten en vergeleken met hun lengtes.
Hier zie je een tabel met de gevonden correlatiecoëfficiënten.
Gebruik de r-tabel.
| | gewicht | bovenwijdte | taille | heup | ruglengte | rugbreedte | vuistomvang | kniehoogte | voetlengte |
| lengte |
Welke variabele heeft de sterkste samenhang met de lengte?
kniehoogte
Kniehoogte, want daarvan is de correlatiecoëfficiënt het grootst.
Welke variabelen hebben met een betrouwbaarheid van % een positieve correlatie met de lengte?
ruglengte, voetlengte, vuistomvang
De lengte van de vrouw heeft met ruglengte, voetlengte en vuistomvang een correlatiecoëfficiënt boven .
Welke variabelen hebben vrijwel geen correlatie met de lengte?
de overige vijf lichaamsmaten
De overige lichaamsmaten, want die hebben een correlatiecoëfficiënt met lengte die tussen en ligt.
Om te onderzoeken of er enig verband bestaat tussen de lengte van een vader en die van zijn zoon zijn de lengtes van vaders en die van hun oudste zoons gemeten op het moment dat die zoons volwassen werden. De gegevens staan in deze tabel.

Teken een spreidingsdiagram (een puntenwolk) bij deze gegevens.
Gebruik Excel.
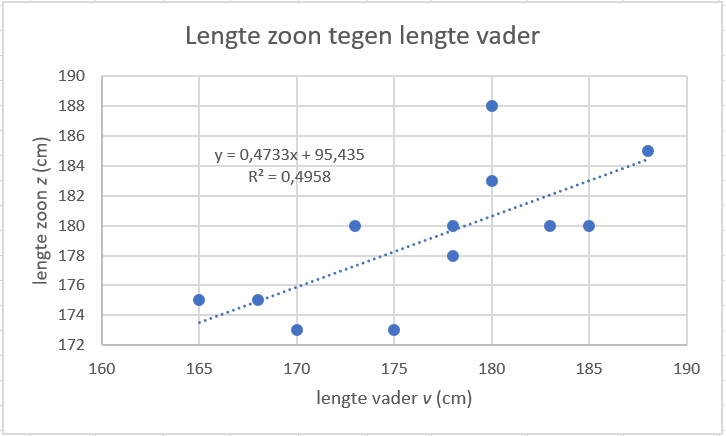
Bereken de correlatiecoëfficiënt in twee decimalen nauwkeurig.
Is er met % betrouwbaarheid sprake van een positieve correlatie?
, dus met % betrouwbaarheid is er een positieve correlatie.
Stel een vergelijking op voor de regressielijn van afhankelijk van .
De regressielijn heeft vergelijking .
Een vader van m lengte krijgt een zoon.
Hoe lang zal die zoon naar verwachting worden?
cm.
In deze figuur staan twee statistische variabelen. Op de horizontale as staat de totale lengte van de Tour de France in kilometer. Op de verticale as staat de gemiddelde snelheid van de winnaar.
Welke samenhang is er tussen de lengte van de Tour de France en de gemiddelde snelheid van de winnaar?
Als je kijkt naar de figuur, lijkt er een (sterke) negatieve samenhang te zijn. Hoe korter de Tour de France, hoe hoger de gemiddelde snelheid van de winnaar.
Maar pas op met oorzaak en gevolg. De oorzaak van een hogere gemiddelde snelheid van de winnaar hoeft niet de afnemende lengte van het parcours te zijn.
Bekijk de drie grafieken:
I
II
III
Twee van de grafieken kun je combineren tot een spreidingsdiagram.
Hoe komt het dat je deze grafieken kunt combineren tot een spreidingsdiagram?
Ze hebben allemaal dezelfde horizontale as met alle jaren waarin de Tour de France gereden is.
De drie grafieken hebben allemaal twee gaten. Wat betekent dit en wat is de oorzaak?
In die jaren is de Tour de France niet gereden vanwege WO I en WO II.
Welke twee (van de drie) grafieken tonen gecombineerd het spreidingsdiagram?
De grafieken I en II.
Geef drie redenen waarom de gemiddelde snelheid van de winnaar los staat van de tourlengte.
Bijvoorbeeld: beter materiaal, toenemend dopinggebruik, het aantal bergen in een etappe, de conditie van de renners, de lengte van een etappe, de grootte van een groep, de concurrentie tussen de renners, het aantal rustdagen.
Bekijk de tabel. In een Amerikaans laboratorium heeft men proeven gedaan waarbij gelet werd op het verband tussen de hoogte van de bewaartemperatuur in graden Fahrenheit en de werkzaamheid van een bepaald geneesmiddel. Bij temperaturen van , , en (Fahrenheit) werden drie porties van gelijk gewicht uit eenzelfde productie dagen bewaard. Na deze periode werd op identieke wijze de werkzaamheid van de porties vastgesteld. De werkzaamheid werd uitgedrukt in percentages van de werkzaamheid zoals die was voor het bewaren.
| bewaartemperatuur (°F) | 30 | 50 | 70 | 90 |
| werkzaamheid (%) | 39, 42, 35 | 32, 26, 33 | 19, 27, 23 | 14, 19, 21 |
In hoeverre is er met een betrouwbaarheid van % sprake van correlatie tussen bewaartemperatuur en werkzaamheid ?
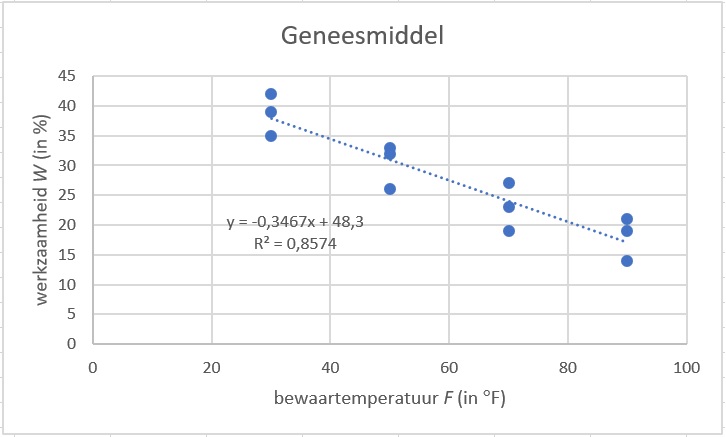
Uit het bijbehorende spreidingsdiagram blijkt al een sterke mate van samenhang en dat wordt bevestigd door de correlatiecoëfficiënt: .
Geef een statistisch verantwoorde schatting voor de werkzaamheid van het geneesmiddel bij een bewaartemperatuur van Fahrenheit.
Formule regressielijn: .
Als dan geldt %
Een vulmachine vult flesjes water. Een aselecte steekproef van flesjes geeft een gemiddelde inhoud van cL. De standaardafwijking is .
Bereken het % betrouwbaarheidsinterval voor het populatiegemiddelde .
Omdat alleen de steekproefstandaardafwijking bekend is, gebruik je de -verdeling met .
Bij een (dubbelzijdige) betrouwbaarheid van % hoort .
Het % betrouwbaarheidsinterval is dus .
Dit levert op: gram.
Laat zien dat je schatting van beter wordt als je een grotere steekproef neemt.
Neem een steekproefgrootte van .
Het % betrouwbaarheidsinterval is dan .
Als groter wordt, wordt juist kleiner en komen de grenzen dichter bij elkaar te liggen.
Je kunt met behulp van correlatie en een regressielijn ook
Hier zie je de resultaten van drie laboranten die de concentratie eiwit in eiersalade elk op hun eigen wijze hebben gemeten vanuit dezelfde monsters.

Je kunt hierbij een spreidingsdiagram maken en de correlatiecoëfficiënt en de regressielijn berekenen.
Als beide meetmethoden vergelijkbare resultaten hebben zal er een hoge positieve correlatie tussen beide bestaan.
Bekijk de twee sets gepaarde gegevens in
Maak een bijpassend spreidingsdiagram en zet daarin de regressielijn.
Zet de resultaten van laborant A op de horizontale as.
Zie figuur, de resultaten van laborant A zijn die van laborant B .
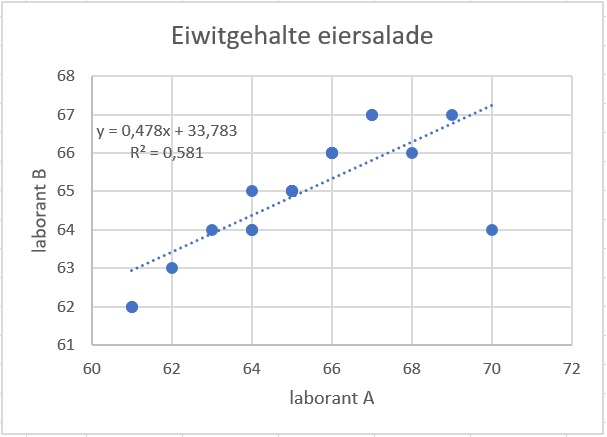
Bereken de correlatiecoëfficiënt en stel met een betrouwbaarheid van % vast of beide meetmethoden overeen komen.
, dus beide meetmethoden komen overeen.
Maakt het verschil als je de gegevens van laborant A op de verticale as van het spreidingsdiagram zet?
Zie figuur, voor de correlatie maakt het geen verschil, maar voor de regressielijn wel.

De 17e meting van laborant A lijkt nogal een uitschieter te zijn.
Hij doet die meting over en vindt nu % eiwit.
Laat zien dat dit een grote invloed heeft op de correlatiecoëfficiënt.
De correlatiecoëfficiënt wordt nu .
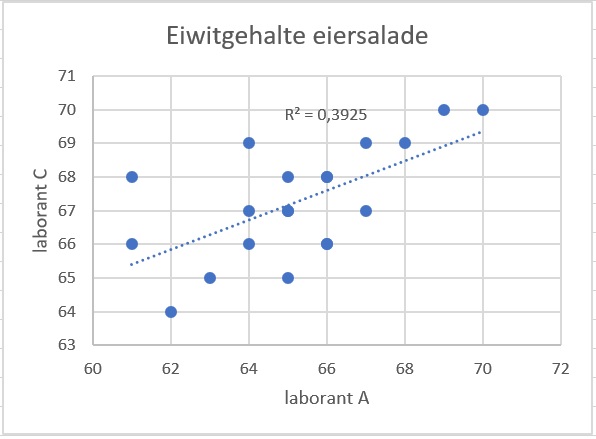
Hier zie je het spreidingsdiagram met de gegevens van laborant C vergeleken met die van laborant B.
Bereken de correlatiecoëfficiënt en ga na dat ook deze correlatie nog steeds voldoet aan de %-betrouwbaarheidsgrens.
Kijk je echter naar de gegevens, dan kun je moeilijk volhouden dat de metingen overeen komen.
Leg dat uit en verklaar wat er waarschijnlijk aan de hand is.
De metingen van laborant C zijn systematisch hoger dan die van laborant B. Hij maakt dus waarschijlijk een systematische fout. Mogelijk is zijn meetinstrument niet geijkt.
Bekijk de puntenwolk BMI-Vetpercentage. Daarin zijn de resultaten weergegeven van een onderzoek onder jongeren. BMI is een getal dat samenhangt met lengte en gewicht, vetpercentage is het percentage van het lichaamsgewicht dat bestaat uit vet.
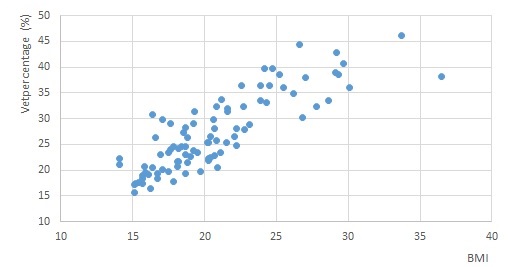
Is er een statistische samenhang? Geef een schatting van de correlatiecoëfficiënt.
Ja, de puntenwolk lijkt iets op een lijn. De correlatiecoëfficiënt zal tussen en liggen.
Is er een oorzakelijk verband?
Waarschijnlijk wel: Als een jongere zwaarder wordt, zal meestal het vetpercentage ook toenemen.
Bij deze puntenwolk kun je een trendlijn tekenen die door en gaat. Welke formule hoort bij deze trendlijn?
Noem het vetpercentage en de BMI . Dan is de formule voor de trendlijn.
Voorspel met behulp van de gevonden trendlijn het vetpercentage van iemand met een BMI van .
%.
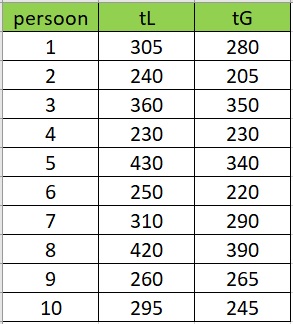
Van een tiental personen worden reactietijden gemeten.
Iemand onderzoekt of de reactietijd op een geluidssignaal afhangt van de reactietijd op een lichtsignaal. Beide reactietijden zijn in milliseconden.
Teken een bijpassend spreidingsdiagram en bepaal de correlatiecoëfficiënt.
Je vindt ( en ):
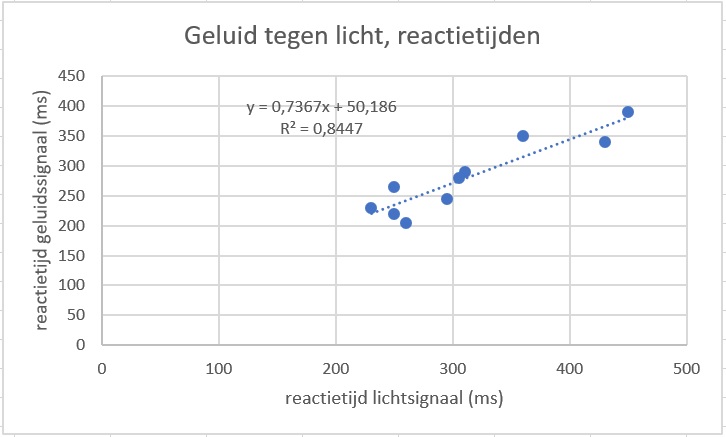
De correlatiecoëfficiënt is .
Kun je met een betrouwbaarheid van % vaststellen dat er inderdaad een positieve correlatie bestaat?
Gebruik de r-tabel.
In dit geval is , dus er is een positieve correlatie.
Iemand reageert op een geluidssignaal na ms.
Hoe snel zal zij op een lichtsignaal reageren?
De regressielijn is: .
Met wordt dit .
Dus ms.
Met het volgende practicum kun je zien hoe je
Hoe sterk de correlatie is, kun je vaststellen met behulp van deze r-tabel. Als jou waarde van verder van afwijkt dan , dan is het verband aangetoond, afhankelijk van de gewenste betrouwbaarheid.