omtrek en oppervlakte van vlakke figuren berekenen, ook met behulp van goniometrie.

werken met gelijkvormigheid van driehoeken;

de stelling van Pythagoras toepassen;

goniometrische verhoudingen sinus, cosinus en tangens toepassen.

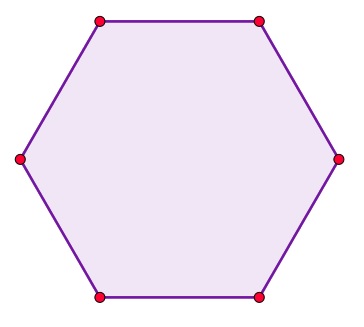
Je ziet hier een regelmatige zeshoek. Alle zijden zijn even lang, in dit geval $2$ cm. Ook alle hoeken zijn even groot.

Hoe groot is de omtrek van deze zeshoek?

$6 * 2 = 12$ cm.

Hoe groot is de oppervlakte van deze zeshoek?

Bekijk de uitleg.

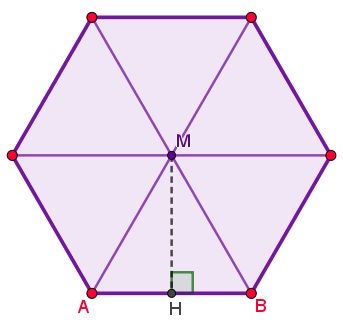
Een regelmatige zeshoek is een zeshoek met gelijke zijden en gelijke hoeken.
Van deze zeshoek is elke zijde $2$ cm.
De omtrek ervan is dus gemakkelijk $6 * 2 = 12$ cm, gewoon de totale lengte van alle zijden samen.

Hoe je de oppervlakte van zo'n zeshoek berekent, zie je in de figuur.
De zeshoek bestaat uit zes gelijke driehoeken, die beslist gelijkbenig zijn en een basis van $2$ cm hebben. Verder weet je de tophoek van zo'n driehoek, want alle zes gelijke tophoeken zitten bij $M$ tegen elkaar en vormen samen een hoek van $360^@$ . Dus bijvoorbeeld $/_AMB = 360^@ // 6 = 60^@$ .
Nu kun je op meerdere manieren verder redeneren:

Met goniometrie: $tan(30^@) = (HB)/(MH) = 1/(MH)$ geeft $MH ~~ 1,732$ .
$Delta MHB$ is een halve rechthoek met oppervlakte $1 * 1,732 // 2 ~~ 0,866$ .
De hele zeshoek bestaat uit $12$ van die driehoeken, dus de oppervlakte is $12 * 0,866 ~~ 10,39$ cm2.

Met de stelling van Pythagoras: omdat $/_AMB = 60^@$ moeten de andere hoeken van $Delta ABM$ ook wel $60^@$ zijn. Dus is $Delta ABM$ gelijkzijdig, alle zijden zijn $2$ cm.
Voor de hoogte $MH$ van deze driehoek geldt $MH^2 + 1^2 = 2^2$ .
Dus $MH = sqrt(2^2 - 1^2) = sqrt(3)$ .
De oppervlakte van $Delta ABM$ is $1/2 * 2 * sqrt(3) = sqrt(3)$ .
De oppervlakte van de zeshoek is $6*sqrt(3) = 6sqrt(3) ~~ 10,39$ cm2.

De oppervlakte van de meeste figuren kun je vinden door ze ofwel te verdelen in rechthoeken en halve rechthoeken en eventueel delen van cirkels, ofwel te omlijsten met een rechthoek en daarvan dan rechthoeken, halve rechthoeken en delen van cirkels af te trekken.
De omtrek van de meeste figuren kun je vinden door de rand in lijnstukken en delen van cirkels te verdelen en de lengte van al die stukken op te tellen.

Soms is het handig om gebruik te maken van formules.
Bijvoorbeeld geldt voor de oppervlakte van elke driehoek $A = 1/2*b*h$ , waarin $A$ de oppervlakte (engels: area), $b$ de lengte van de basis en $h$ de lengte van de hoogte op die basis is. In de Theorie vind je een overzicht van die formules.

Bekijk de Uitleg.
De oppervlakte van de zeshoek wordt bepaald door van $Delta ABM$ de tophoek $/_AMB$ te berekenen.
Je kunt echter ook in plaats daarvan $/_BAM$ berekenen en daarmee de oppervlakte uitrekenen.

Hoe kun je $/_BAM$ berekenen?

De zeshoek bestaat uit zes driehoeken waarvan de hoekensom $180^@$ is.
Alle hoeken van de zeshoek zijn gelijk en hun hoekensom is $6*180^@ - 360^@ = 720^@$ (want de tophoeken zijn geen hoeken van de zeshoek, dus die gaan er af).
De hoeken van de zeshoek zijn $12$ hoeken die dezelfde grootte hebben als $/_BAM$ , dus $/_BAM = 720^@ // 12 = 60^@$ .

Hoe kun je met behulp van $/_BAM$ de oppervlakte van de zeshoek berekenen?

Bijvoorbeeld zo: $tan(60^@) = (MH)/1$ , dus $MH ~~ 1,732$ en $opp(Delta ABM) = 1/2 * 2 * 1,732 ~~ 1,732$ cm2.
Nog even maal $6$ en het is weer gepiept.

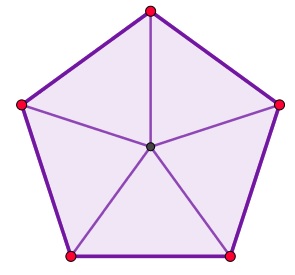
Ook een regelmatige vijfhoek kun je opdelen in driehoeken, zie de figuur.

Bereken de oppervlakte van deze vijfhoek als alle zijden $3$ cm lang zijn.

Er zijn nu vijf gelijkbenige driehoeken met een basis van $3$ cm en een tophoek van $360^@ // 5 = 72^@$ .
Voor de hoogte $h$ van zo'n driehoek geldt: $tan(36^@) = (1,5)/h$ , dus $h ~~ 2,065$ .
De oppervlakte van de zeshoek is $6 * 1/2 * 3 * 2,065 ~~ 18,58$ cm2.

Je ziet hier twee verschillende driehoeken.

Waarom hebben ze dezelfde oppervlakte?
Hoe groot is die oppervlakte?

Omdat de basis en de hoogte van beide driehoeken hetzelfde zijn.
De oppervlakte van elk van beide driehoeken is $1/2 * 5 * 6 = 15$ cm2.

Welke van beide driehoeken heeft de grootste omtrek?

De rechter driehoek.

Van een driehoek $Delta ABC$ is $AB = 7$ cm, $AC = 4$ cm en $/_A = 40^@$ .

Bereken de oppervlakte en de omtrek van deze driehoek.

Maak een schets van de driehoek, of misschien wel een nette tekening zodat je lengtes en hoeken kunt nameten om te kijken of je berekeningen goed zijn.

Neem $AB$ als basis en noem de hoogte $CD$ .
Dan is $CD = 4*sin(40^@) ~~ 2,57$ cm.
$opp(Delta ABC) = 1/2 * 7 * 2,57 ~~ 9,00$ cm2.

Voor de omtrek moet je de lengte van zijde $BC$ weten.
Nu is $AD = 4*cos(40^@) ~~ 3,06$ zodat $DB ~~ 3,94$ cm.
En $BC = sqrt(2,57^2 + 3,94^2) ~~ 4,70$ cm.
De omtrek is ongeveer $4 + 7 + 4,70 = 15,70$ cm.

Van veel figuren kun je de oppervlakte berekenen door opdelen of omlijsten.
Bekijk deze figuren.

Bereken de oppervlakte en de omtrek van deze drie figuren.

Linker figuur:
Door opdelen vind je als oppervlakte: $1*4 + 2*2 + 1/2*4*4 + 1/2*3*2 = 19$ cm2.
De omtrek is: $6 + 1 + 2 + sqrt(4^2+4^2) + sqrt(2^2+3^2) = 9 + sqrt(32) + sqrt(13)$ cm.

Middelste figuur:
Door omlijsten vind je als oppervlakte: $5*6 - 1/2*6*2 - 1/2*5*2 - 1/2*5*4 = 9$ cm2.
De omtrek is: $sqrt(4^2+2^2) + sqrt(2^2+2^2) + sqrt(5^2+2^2) + sqrt(5^2+4^2) = sqrt(20) + sqrt(8) + sqrt(29) + sqrt(41)$ cm.

Rechter figuur:
Door omlijsten vind je als oppervlakte: $5*6 - 1/2*2*2 - 1/2*4*2 - 1/2*2*2 - 4*2 = 14$ cm2.
De omtrek is: $sqrt(2^2+2^2) + sqrt(4^2+2^2) + 1 + 3 + 4 + sqrt(2^2+2^2) = 8 + 2*sqrt(8) + sqrt(20)$ cm.

Soms is het handig om gebruik te maken van formules.
Hier vind je een overzicht van de belangrijkste formules.

rechthoek	halve rechthoek	driehoek
oppervlakte: $lb$ omtrek: $2l + 2*b$	oppervlakte: $1/2lb$ omtrek: $l + b + sqrt(l^2 + b^2)$	oppervlakte: $1/2bh$ of $1/2bc*sin(alpha)$ omtrek: de lengtes van de zijden optellen
parallellogram	trapezium	cirkel	cirkelsector
oppervlakte: $b*h$ omtrek: de lengtes van de zijden optellen	oppervlakte: $1/2(a+b)h$ omtrek: de lengtes van de zijden optellen	oppervlakte: $pir^2$ of $1/4pid^2$ omtrek: $2pir$ of $pid$	oppervlakte: $(alpha)/(360^@)pir^2$ omtrek: $(alpha)/(360^@)2pir + 2r$

Gegeven $Delta ABC$ met $/_A = 50^@$ , $AB = 8$ cm en $AC = 5$ cm.

Bereken de oppervlakte van deze driehoek in mm2 nauwkeurig.

Maak een schets en zet er meteen een handig gekozen hoogtelijn in.
In dit geval is dat $CD$ .

In $Delta ADC$ geldt: $sin(50^@) = (CD)/5$ , zodat $CD = 5*sin(50^@) ~~ 3,830$ cm.
De oppervlakte van $Delta ABC$ is dus: $~~1/2*8*3,830~~15,32$ cm2

Je ziet in Voorbeeld hoe je van $Delta ABC$ de oppervlakte berekent.

Bereken de omtrek van deze driehoek.

In $Delta ADC$ is $cos(50^@) = (AD)/(AC) = (AD)/5$ , dus $AD = 5 cos(50^@) ~~ 3,21$ cm.
Dit betekent dat $DB ~~ 8 - 3,21 ~~ 4,79$ cm.
En dus is met de stelling van Pythagoras $BC ~~ sqrt(3,83^2 + 4,79^2) ~~ 6,13$ .
De omtrek van deze driehoek is daarmee ongeveer $5+8+6,13 = 19,13$ cm.

Bekijk de oppervlakteberekening nog eens.
Neem aan dat $/_A = alpha$ , $AB = c$ en $AC = b$ .

Toon aan dat voor de oppervlakte van $Delta ABC$ dan geldt: $opp(Delta ABC) = 1/2 bc sin(alpha)$ .

In $Delta ADC$ is $sin(alpha) = (CD)/(AC) = (CD)/b$ , dus $CD = b sin(alpha)$ cm.
De oppervlakte van deze driehoek is daarmee $1/2 * c * bsin(alpha) = 1/2 bc sin(alpha)$ .

Van $Delta PQR$ is $/_R = 67^@$ , $PR = 10$ cm en $QR = 12$ cm.

Bereken de oppervlakte en de omtrek van deze driehoek.

Voor de oppervlakte kun je net zo werken als in het voorbeeld, je kunt ook de formule van de vorige opgave gebruiken.
$opp(Delta PQR) = 1/2 * 10 * 12 * sin(67^@) ~~ 55,23$ cm2.

Voor de omtrek moet je ook de derde zijde uitrekenen.
De hoogtelijn $QT$ heeft een lengte van $12*sin(67^@) ~~ 11,05$ en $TR = 12*cos(67^@)~~ 4,69$ cm.
Dus is $PQ = sqrt(11,05^2 + (10-4,69)^2) ~~ 12,26$ cm.
De omtrek is daarom ongeveer $10+12+12,26 ~~ 34,3$ cm.

Je ziet hier een afdekplaatje, alle afmetingen zijn in mm.
R10 betekent dat de cirkel een straal van $10$ (hier: mm) heeft.
Bereken de oppervlakte van dit plaatje in mm2 nauwkeurig.

Verdeel de figuur en zet letters bij hoekpunten.

Van $Delta ABE$ weet je $/_A = 80^@$ en $AB = 40$ mm.

Dus is $sin(80^@) = (BE)/(AB) = (BE)/(40)$ , zodat $BE = 40*sin(80^@) ~~ 39,4$ mm.
Zo is ook: $AE ~~ 6,9$ mm.

De gezochte oppervlakte is daarom $1/2 * 39,4 * 6,9 + 39,4 * (40 - 6,9) + 1/2 * pi * 10^2 ~~ 1597$ mm2.

Bekijk het plaatje in Voorbeeld.

Waarom is $AE ~~ 6,9$ ?

$cos(80^@) = (AE)/(AB) = (AE)/(40)$ , zodat $AE = 40*cos(80^@) ~~ 6,9$ mm.

Leg uit hoe uiteindelijk de oppervlakte van het plaatje is berekend.

$opp(Delta ABE) = 1/2 * 39,4 * 6,9$ mm2.
$opp(BCDE) = BE * ED = 39,4 * (40 - 6,9)$ mm2.
$opp(halve cirkel) = 1/2 * pi * 10^2$ mm2.

Hoeveel bedraagt de totale omtrek van dit plaatje in mm nauwkeurig?

$2*40 + 39,4 + 40 - 2*10 - 6,9 + 1/2 * pi * 20 ~~ 163,9$ mm.

Je ziet hier drie vormen. Neem aan dat alle hoeken die recht lijken dat ook zijn en alle bogen die op cirkelbogen lijken echte cirkelbogen zijn. Alle afmetingen zijn in cm.

Bereken van elke vorm de oppervlakte in mm2 en de omtrek in mm nauwkeurig.

Linker figuur:
Omtrek is $10 + 8 + sqrt(7^2+11^2) + 11 + sqrt(3^2+8^2) ~~ 50,6$ cm.
Oppervlakte is $1/2 * 3 * 8 + 7*8 + 1/2 * 7 * 11 = 106,5$ cm2.

Middelste figuur:
Omtrek is $pi * 8 + 5 + 11 + 5 + 11 ~~ 57,1$ cm.
Oppervlakte is $pi * 4^2 + 11*13 ~~ 193,27$ cm2.

Rechter figuur:
Omtrek is $2*15 + 4*1 + 2*pi*4 ~~ 59,1$ cm.
Oppervlakte is $6*15 - 2*pi*2^2 ~~ 64,87$ cm2.

Je ziet hier twee vormen. Neem aan dat alle hoeken die recht lijken dat ook zijn en alle bogen die op cirkelbogen lijken echte cirkelbogen zijn. Alle afmetingen zijn in cm.

Bereken van elke vorm de oppervlakte in mm2 en de omtrek in mm nauwkeurig.

Linker figuur is een rechthoekige driehoek van $26$ cm bij $26*tan(40^@) ~~ 21,82$ cm minus een kwart cirkel:
Omtrek is $20 + 15,82 + sqrt(26^2+21,82^2) + 1/4*pi*12 ~~ 79,34$ cm.
Oppervlakte is $1/2 * 26 * 21,82 - 1/4 * pi * 6^2 ~~ 255,34$ cm2.

Rechter figuur is driehoek met hoogte $30*sin(40^@) ~~ 19,28$ , minus cirkel:
Omtrek is $30 + 26 + sqrt(3,02^2 + 19,28^2) + pi*10 ~~ 106,9$ .
Oppervlakte is $1/2*26*19,28 - pi*5^2 ~~ 172,15$ cm2.

Een atletiekbaan bestaat uit twee rechte stukken van $100$ m en twee halve cirkels die ook elk een lengte hebben van $100$ m.
Het middenterrein van die atletiekbaan is een rechthoek met op beide uiteinden halve cirkels.

Hoe groot is de oppervlakte van dit binnenterrein?

Teken de situatie en zet de gegevens er in.

Beide cirkelbogen vormen een cirkel met een omtrek van $200$ m en hebben dus een diameter van $200/(pi)~~63,66$ m.

De oppervlakte van het binnenterrein is ongeveer $100*63,66 + 1/4 pi*63,66^2 ~~ 9549,30$ m2.

Een driehoekig afdekplaatje heeft twee zijden van $412$ mm die een hoek van $30^@$ met elkaar maken.

Hoe groot is de oppervlakte van dit plaatje?

Teken de situatie en zet de gegevens er in, de driehoek is gelijkbenig en de hoogtelijn kies je op de symmetrieas.

De hoogte van het plaatje is $412 * cos(15^@) ~~ 398$ mm en de halve basis is $412 * sin(15^@) ~~ 106,6$ mm.

De oppervlakte van het plaatje is ongeveer $1/2 * 213 * 398 = 42436$ mm2.

Je ziet hier een foto van een huis met een zogenaamd mansardedak. Het dak bestaat uit vier delen die allemaal de vorm van een rechthoek van $2,5$ m bij $10$ m hebben (houd geen rekening met de dakkapel boven de voordeur en de schoorsteen). De onderste twee delen van het dak maken een hellingshoek van $65^@$ met een horizontaal vlak. De vloer van het huis is een rechthoek van $6$ m bij $10$ m. De dakgoot zit op $3$ m boven de grond.

Maak een tekening van de zijgevel op schaal met de maten erin. Je kunt ze afleiden uit bovenstaande tekst.

In de figuur is $A B = B C = C D = D E = 3$ en $E F = F G = G H = H A = 2,5$ . Verder zijn er twee hoeken gegeven.

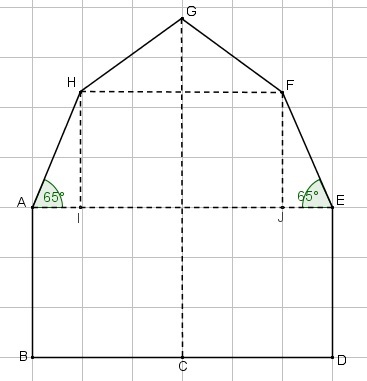
Bereken de hoogte van het huis in cm nauwkeurig.

$H I = 2,5 \cdot \sin (65) \approx 2,266$
$A I = 2,5 \cdot \cos (65) \approx 1,057$
Als $K$ het snijpunt is van $H F$ en $G C$ , dan is $H K \approx 3 - 1,057 = 1,943$ .
$G K \approx \sqrt{{2,5}^{2} - {1,943}^{2}} \approx 1,57$ .
De gevraagde hoogte is $C G \approx 3 + 2,27 + 1,57 = 6,84$ m.

Vanwege de druk van eventuele sneeuw op het dak, mag volgens de aannemer het dak geen hellingshoek lager dan $35^@$ hebben, want anders dan moet het dak verstevigd worden.

Bereken de hellingshoek van de bovenste twee delen van het dak in graden nauwkeurig en beslis of het dak verstevigd moet worden.

De hellingshoek is $/_FHG$ en $cos(/_FHG) ~~ (1,943)/(2,5)$ zodat $/_FHG ~~ 39^@$ , dus versteviging is niet nodig.

In de Amsterdamse St. Gabriëlskerk vind je dit veelkleurige vijfhoekige glas-in-loodraam. Het is ontworpen en vervaardigd door de Haarlemse glazenier W. Bogtman. Het complete vijfhoekige raam (dus de buitenste vijfhoek) past precies in een cirkel met een straal van $1$ m. Alle zijden van het raam zijn even lang.

Teken deze vijfhoek en licht toe hoe je dat doet.

Cirkel met middelpunt $M$ en straal $1$ tekenen en dan bij $M$ vijf gelijke hoeken van $(360^@)/5 = 72^@$ tekenen. De snijpunten van de benen van die hoeken met de cirkel moet je nog met elkaar verbinden.

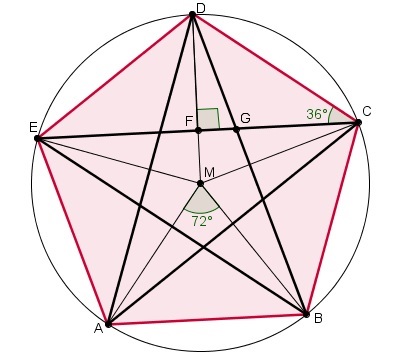
Bereken de lengtes van de zijden van deze vijfhoek in mm nauwkeurig.

Werk in $Delta MAB$ en teken daarin hoogtelijn $M P$ .
Dan is $M P = \cos (36)$ en $A P = \sin (36)$ . De zijden van de vijfhoek hebben een lengte van $2 \cdot \sin (36) \approx 1,176$ m, dus $1176$ mm.

Bereken de totale oppervlakte van het glas-in-loodraam in cm2 nauwkeurig.

De oppervlakte is $5*sin(36^@)*cos(36^@) ~~ 2,378$ m2.

In het vijfhoekige raam zit een vijfpuntige ster van metalen strips.

Hoeveel meter van die strips is er in totaal nodig voor deze vijfpuntige ster? Geef je antwoord in mm nauwkeurig.

Werk in $Delta MAD$ . Daarin is $A D = 2 \cdot \sin (72)$ . Het kruis bestaat uit vijf diagonalen van de vijfhoek en heeft dus een lengte van $5 \cdot 2 \cdot \sin (72) \approx 9,511$ m.

In feite bestaat deze ster uit $15$ lijnstukken met twee verschillende lengtes. Bereken die twee verschillende lengtes in mm nauwkeurig.

$C F = 2 \cdot \sin (36) \cdot \cos (36) \approx 0,951$
$D F = 2 \cdot \sin (36) \cdot \sin (36) \approx 0,691$
$/_CDG = 180^@ - 2 ⋅ 36^@ = 108^@$ , dus $/_FGD = 72^@$ .
$F G = D F / \tan (72) \approx 0,225$
De éne lengte is $2 \cdot F G \approx 0,449$ m en de andere is $G C \approx 0,951 - 0,225 = 0,726$ m.

Met deze applet maak je regelmatige veelhoeken. Ze passen in een cirkel met straal $1$ . Je kunt een regelmatige $n$ -hoek opdelen in $n$ gelijke en gelijkbenige driehoeken waarvan de tophoek het middelpunt van de cirkel is waar de andere hoekpunten op liggen.

Met behulp van goniometrie kun je van zo'n driehoek de oppervlakte berekenen. En daarmee bereken je ook de oppervlakte van de veelhoek. En zo kun je zelfs $pi$ benaderen...

Bekijk de applet. Als je $n = 5$ instelt zie je een regelmatige vijfhoek.

In hoeveel gelijke en gelijkbenige driehoeken kun je deze figuur opdelen?

$5$

Hoe groot zijn de hoeken van zo'n driehoek?

Eén tophoek van $360^@ // 5 = 72^@$ en twee basishoeken van $54^@$ .

Bereken de oppervlakte van zo'n driehoek.

De hoogte is $cos(36^@)$ en de basis is $2*sin(36^@)$ .

De oppervlakte is daarom $sin(36^@) * cos(36^@) ≈ 0,475$ .

Hoe groot is de oppervlakte van de vijfhoek?

$5 * sin(36^@) * cos(36^@) ≈ 2,378$

Bekijk de applet nog eens.

Als je $n=6$ instelt zie je een regelmatige zeshoek. Bereken op dezelfde manier als in de voorgaande opgave de oppervlakte van de regelmatige zeshoek.

$6*sin(30°)*cos(30°)~~2,598.$

Neem nu $n=8$ . Bereken de oppervlakte van de regelmatige achthoek.

$8*sin(22,5°)*cos(22,5°)~~2,828$ .

Neem nu $n=10$ . Bereken de oppervlakte van de regelmatige tienhoek.

$10*sin(18°)*cos(18°)~~2,939$ .

Neem nu $n=100$ . Bereken de oppervlakte van de regelmatige honderdhoek.

$100*sin(1,8°)*cos(1,8°)~~3,140$ .

Als je $n$ steeds kon blijven vergroten, welk getal ga je dan steeds meer benaderen?

Het getal $pi$ .

Oppervlakte mal

Zie bijgaande figuur. Het is de tekening van een mal die je op school moet vervaardigen. De reeds opgegeven maten zijn allen in cm.

Bereken maat $a$ .

$a~~30,2$ cm

Zie ook de figuur hiernaast.
$tan(63,5°)=(FG)/(AG)$ geeft $AG=(FG)/(tan(63,5°))=50/(tan(63,5°))~~24,9$
$/_EDI=180°-120,3°=59,7°$
$tan(/_EDI)=(EI)/(DI)=>DI=(EI)/(tan(/_EDI))=34/(tan(59,7°))~~19,9$
$a=100-AG-HJ-JB~~100-19,9-24,9-25=30,2$ cm.

Bereken maat $b$ .

$b~~74,4$ cm

$b^2=(AH)^2+(EH)^2=(55,1)^2+50^2$ geeft $b~~74,4$ cm.

Van $Delta ABC$ is gegeven $AB = 30$ cm, $BC = 12$ cm en $/_B = 65^@$ .
Bereken van deze driehoek de omtrek in mm en de oppervlakte in mm2 nauwkeurig.

De omtrek is ongeveer $69,2$ mm.
De oppervlakte is ongeveer $163,14$ mm2.

De hoogte is $CD = 12 sin(65^@) ~~ 10,88$ cm en $BD = 12 cos(65) ~~ 5,07$ cm.
Omdat dan $AD = 24,93$ cm is $AC = sqrt(24,93^2 + 10,88^2) ~~ 27,20$ cm.
De omtrek is ongeveer $27,20+30+12 ~~ 69,2$ mm.
De oppervlakte is ongeveer $1/2 * 30 * 10,88 ~~ 163,14$ mm2.

Een regelmatige zevenhoek heeft zijden die $2$ cm lang zijn.

Bereken de oppervlakte van de zevenhoek in mm2 nauwkeurig.

De oppervlakte van de zevenhoek is $7 * 1/2 * 2 * 2,07 ~~ 14,54$ cm2.

Bekijk de figuur.
$M$ is het midden van de zevenhoek, het gemeenschappelijke punt van alle zeven gelijke en gelijkbenige driehoeken waaruit de zevenhoek bestaat.
$/_ AMB = 360^@ // 7 = 51,4 ^@$ .
De hoogte $MH$ van $Delta ABM$ is $MH = 1/(tan(25,7^@)) ~~ 2,08$ cm.
De oppervlakte van de zevenhoek is $7 * 1/2 * 2 * 2,07 ~~ 14,54$ cm2.

Deze vorm bestaat uit een rechthoekige driehoek waaraan driekwart van een cirkel is bevestigd.
Alle afmetingen zijn in cm.

Bereken de omtrek en de oppervlakte van deze vorm.

Oppervlakte $~~ 582,52$ cm2.

Omtrek $~~ 105,6$ cm.

Van de rechthoekige driehoek is de kortste rechthoekszijde $24$ cm.
De andere rechthoekszijde is daarom $(24)/(tan(40^@))~~ 28,60$ .

De oppervlakte is $1/2 * 24 * 28,60 + 3/4 * pi * 12^2 ~~ 682,52$ cm2.

De omtrek is $12 + (28,60 - 12) + sqrt(12^2 + (28,60 - 12)^2) + 3/4 * pi * 24 ~~ 105,6$ cm.