gelijkvormigheid, de stelling van Pythagoras en goniometrie toepassen in ruimtelijke figuren.

de verschillende ruimtelijke basisfiguren;

werken met gelijkvormigheid van driehoeken en de stelling van Pythagoras;

goniometrische verhoudingen sinus, cosinus en tangens, de sinusregel en de cosinusregel.

In Helmond staan $18$ kubusvormige paalwoningen. Piet Blom heeft deze ontworpen en later ook in Rotterdam geplaatst. De woning bestaat uit een kubus die op zijn punt op een zeshoekige entree met een trap staat.
De lengte van alle zijden van de kubus is $7,5$ m.

Bereken de lengte van een diagonaal van de kubus.

$12,99$ m.

In de figuur is de kubus voor de duidelijkheid gedraaid. $AC^2$ $=$ $7,5^2+7,5^2=112,5$ $AC$ $=$ $sqrt(112,5)~~10,6$ m $AG^2$ $=$ $AC^2+CG^2=112,5+7,5^2=168,75$ $AG$ $=$ $sqrt(168,75)~~12,99$ m.

Het probleem bij Verkennen heb je waarschijnlijk wel meteen kunnen oplossen. Daarbij heb je dan gebruik gemaakt van kennis over ruimtelijke figuren. Je moet weten wat een balk is, waar de rechte hoeken in een balk zitten, en dergelijke meer.

Je noemt een ruimtelijke figuur vaak een lichaam. Zo'n lichaam heeft één of meer grensvlakken, die vaak plat, maar ook gebogen kunnen zijn. Gebogen grensvlakken heb je bij een bol, een kegel, een cilinder.

Lichamen die alleen uit platte grensvlakken bestaan heten veelvlakken. Deze hebben hoekpunten en ribben. Ook zijn er dan vaak diagonalen in twee soorten: zijvlaksdiagonalen en lichaamsdiagonalen.
Het veelvlak $A B C D E F . G H I J K L$ hiernaast bijvoorbeeld heet een regelmatig zeshoekig prisma. Dat komt omdat van dit lichaam:

het grondvlak en het bovenvlak congruente regelmatige zeshoeken zijn;

alle opstaande zijvlakken rechthoeken zijn.

In feite is elke doorsnede van dit lichaam die evenwijdig is met het grondvlak een regelmatige zeshoek.
Verder zie je diagonaalvlak $B E K H$ met daarin lichaamsdiagonaal $B K$ .

In de Theorie vind je een overzicht van de belangrijkste lichamen en hun eigenschappen. Ook worden er de rekentechnieken die je al kent nog eens genoemd.

Bekijk de Uitleg. Je ziet er een voorbeeld van een prisma. Neem aan dat van het grondvlak alle zijden $4$ cm zijn en dat de opstaande ribben allemaal $6$ cm lang zijn.

Hoeveel hoekpunten, hoeveel ribben en hoeveel grensvlakken heeft dit prisma?

$12$ hoekpunten, $18$ ribben en $8$ grensvlakken.

Hoeveel zijvlaksdiagonalen heeft dit prisma? En hoeveel lichaamsdiagonalen?

Zijvlaksdiagonalen:
Elk opstaand zijvlak heeft er $2$ , elke zeshoek heeft er $(6*3)/2=9$ (vanuit elk hoekpunt kun je er drie trekken, maar dan tel je wel elke diagonaal dubbel). Dat is in totaal $6*2 + 2*9 = 30$ .

Elke lichaamsdiagonaal ligt in een verticaal diagonaalvlak, in elk verticale diagonaalvlak liggen er $2$ . In een bovenaanzicht zie je dat er $9$ verticale diagonaalvlakken zijn en dus zijn er in totaal $9 * 2 = 18$ lichaamsdiagonalen.

Teken het grondvlak van dit prisma op ware grootte. Leg uit, waarom diagonaal $B E = 8$ cm en diagonaal $B F = 4 \sqrt{3}$ cm.

Teken een cirkel met straal $4$ en pas daarop zes punten af die $4$ cm van elkaar af liggen. Je krijgt dan de regelmatige zeshoek $A B C D E F$ .

Zo'n regelmatige zeshoek bestaat uit zes gelijkzijdige driehoeken met zijden van $4$ cm. Elke gelijkzijdige driehoek kun je verdelen in twee congruente driehoeken met zijden van $4$ , $2$ en $\sqrt{12} = 2 \sqrt{3}$ cm. Daaruit volgen de lengtes van de lichaamsdiagonalen.

Teken het diagonaalvlak $B E K H$ op ware grootte. Bereken de grootte van $/_ EBK$ in graden nauwkeurig.

Dit diagonaalvlak is een rechthoek van $8$ cm bij $6$ cm.

Omdat $tan(/_ EBK) = 6/8 = 0,75$ is $/_ EBK ~~ 37^@$ .

Teken het diagonaalvlak $B F L H$ op ware grootte en bereken de grootte van $/_ FBL$ in graden nauwkeurig.

Dit diagonaalvlak is een rechthoek van $4 \sqrt{3}$ cm bij $6$ cm.

Omdat $tan(/_ FBL) = 6/(4sqrt(3))$ is $/_ FBL ~~ 41^@$ .

Je ziet hier een ander prisma, de figuur staat ook op het werkblad. Hier zijn het voorvlak en het achtervlak congruente gelijkzijdige driehoeken met zijden van $6$ cm. Alle andere grensvlakken zijn vierkanten.

Waarom heeft dit prisma geen lichaamsdiagonalen?

Omdat elke verbinding tussen twee hoekpunten in een grensvlak ligt.

Hoeveel zijvlaksdiagonalen heeft dit prisma?

$3 \cdot 2 = 6$

$M$ is het midden van ribbe $C F$ . Teken $Δ A B M$ zowel in de figuur als op ware grootte.

Doen. Je kunt de lengte van $A M$ en $B M$ opmeten in een vierkant van $6$ cm bij $6$ cm, of deze lengte berekenen. Je vindt $A M = B M = \sqrt{6^{2} + 3^{2}} = \sqrt{45}$ .

Bereken de grootte van $/_ AMB$ in graden nauwkeurig.

Maak in $Δ A B M$ een rechte hoek door hoogte $M N$ te tekenen. Dan is $sin(/_ NMB) = 3/(sqrt(45))$ en dus $/_ NMB ~~ 26,6^@$ .

En dus is $/_ AMB ~~ 53^@$ .

Werkblad bij opgave

Het lichaam hiernaast is een regelmatige zeszijdige piramide $A B C D E F . T$ . Alle zijden van het grondvlak zijn $6$ cm. Alle opstaande ribben zijn $24$ cm.

Heeft deze piramide lichaamsdiagonalen? En zijvlaksdiagonalen? En diagonaalvlakken?

Alleen $6$ zijvlaksdiagonalen in het grondvlak. En daarbij horen ook $6$ diagonaalvlakken.

Bereken de grootte van $/_ BTE$ in graden nauwkeurig.

Maak in $Δ B T E$ een rechte hoek door hoogte $T S$ te tekenen. Dan is $sin(/_ BTS) = 6/24 = 0,25$ en dus $/_ BTS ~~ 14,5^@$ .

En dus is $/_ BTE ~~ 29^@$ .

Bereken de grootte van $/_ BTF$ in graden nauwkeurig.

Maak in $Δ B T F$ een rechte hoek door hoogte $T P$ te tekenen. Dan is $sin(/_ BTP) = (3sqrt(3))/24$ en dus $/_ BTP ~~ 12,5^@$ .

En dus is $/_ BTE ~~ 25^@$ .

Een lichaam is een ruimtelijke figuur. Een lichaam heeft één of meer (eventueel gebogen) grensvlakken. Je ziet hier een overzicht van enkele veel voorkomende lichamen.

Een lichaam met alleen platte grensvlakken heet een veelvlak. Een veelvlak heeft ribben en hoekpunten. Piramides en prisma's hebben een grondvlak en een hoogte.
Veel veelvlakken hebben ook diagonaalvlakken, die twee overstaande evenwijdige ribben verbinden. En verder zijn en vaak zijvlaksdiagonalen en lichaamsdiagonalen.

In lichamen kun je lengtes van lijnstukken en hoeken berekenen met behulp van:

de stelling van Pythagoras in rechthoekige driehoeken;

gelijkvormige driehoeken;

goniometrie in rechthoekige driehoeken;

de sinusregel en de cosinusregel in willekeurige driehoeken.

Hier zie je een balk $A B C D . E F G H$ . In het diagonaalvlak $A C G E$ is de lichaamsdiagonaal $A G$ getekend. Ook zie je daarin lijnstuk $A M$ , waarbij $M$ het midden van $E G$ is. In deze figuur is $A B = 8$ cm, $B C = 6$ cm en $C G = 5$ cm.

Bereken de lengte van lijnstuk $C N$ in twee decimalen nauwkeurig.

Het lijnstuk waarvan je de lengte wilt berekenen ligt in diagonaalvlak $A C G E$ en dat is een rechthoek met zijden $A C = 10$ cm en $C G = 5$ cm.

Met behulp van de stelling van Pythagoras kun je de lengte van zowel $A G$ als $C M$ berekenen. En dan kun je met gelijkvormigheid werken. Zie je al welke driehoeken gelijkvormig zijn?

Je vindt $C N \approx 4,71$ cm.

Bekijk Voorbeeld.

Leg uit waarom $A C = 10$ cm.

$A B C D$ is een rechthoek van $8$ bij $6$ cm. Dus is driehoek $A B C$ een rechthoekige driehoek waarin je de stelling van Pythagoras kunt doen: $A C = \sqrt{8^{2} + 6^{2}} = 10$ .

Bereken nu zelf de lengtes van $A G$ en $C M$ .

Teken eventueel rechthoek $A C G E$ .

$A G = \sqrt{10^{2} + 5^{2}} = \sqrt{125}$ en $C M = \sqrt{5^{2} + 5^{2}} = \sqrt{50}$ cm.

Welke twee gelijkvormige driehoeken vind je in diagonaalvlak $A C G E$ ? Leg uit waarom ze gelijkvormig zijn.

$Δ A C N \sim Δ G M N$ omdat $/_ ANC = /_ GNM$ (overstaande hoeken) en $/_ CAN = /_ MGN$ (Z-hoeken). Dus hebben beide driehoeken gelijke hoeken en zijn ze gelijkvormig.

Bereken de lengte van $C N$ .

Omdat $A C : G M = 2 : 1$ en $Δ A C N \sim Δ G M N$ zijn de zijden van $Δ A C N$ $2$ keer zo groot dat die van $Δ G M N$ . En dus is $C N = \frac{2}{3} C M = \frac{2}{3} \sqrt{50} \approx 4,71$ .

Je kunt de lengte van $CN$ ook berekenen door bijvoorbeeld in $Delta ACN$ de sinusregel toe te passen.
Laat zien hoe je dan te werk gaat.

Je hebt $AC = 10$ al berekend.
Uit $tan(/_ CAN) = 5/10$ volgt dat $/_ CAN ~~ 26,6^@$ .
Uit $tan(/_ ACM) = 5/5$ volgt dat $/_ ACM = 45^@$ .
Dus is $/_ ANC ~~ 180^@ - 26,6^@ - 45^@ = 108,4^@$ .
Sinusregel: $10/(sin(108,4^@)) = (CN)/(sin(26,6^@))$ geeft $CN~~4,71$ .

Je ziet de nestkast van een torenvalk.
Het met zink beklede dak is een vierkant van $6$ cm bij $6$ cm.
De achterwand is een rechthoek van $5$ bij $8$ cm en het grondvlak een rechthoek van $5$ bij $4$ cm. Van de voorkant van de nestkast is de onderste helft dichtgemaakt met een rechthoekig plankje van $5,6$ bij $3,3$ cm. De plankjes en het zinken dak zijn $3$ mm dik.

Welke naam heeft het lichaam dat de binnenruimte van deze nestkast voorstelt?

Een prisma (de zijwand is dan het grondvlak van dit prisma).

Hoe groot zijn de zijden van een zijwand van deze nestkast?

De onderste zijde moet $4,3$ cm lang zijn (in verband met de dikte van het hout).
De voorste zijde is moet $6,3$ cm lang zijn (de onderste helft is dichtgemaakt met een plankje dat een hoogte van $3,3$ cm heeft en waarvan de onderste $0,3$ cm te maken heeft met de dikte van het hout).
De achterste zijde moet $8,3$ cm lang zijn.
De schuine bovenzijde wordt $sqrt(4,3^2 + 2^2) ~~ 4,7$ cm lang.

Hoe groot zijn de hoeken van een zijwand van deze nestkast?

De onderste twee hoeken zijn recht.
Voor de bovenste hoek tegen de achterzijde geldt $tan(alpha) = (4,3)/2$ zodat $alpha ~~ 65^@$ is.
De bovenste hoek aan de voorzijde is daarom ongeveer $180^@ - 65^@ = 115^@$ .

Deze tekening stelt een tent voor. De afmetingen zijn in de figuur gegeven. Ga er van uit dat de lichter gekleurde stippellijnen in een snijpunt loodrecht op elkaar staan.

Welke ruimtelijke figuren herken je in de vorm van deze tent?
Aan de voorzijde zie je twee schuin staande driehoeken. Bereken daarvan de afmetingen.

De figuur bestaat uit twee halve piramides aan de voorkant en de achterkant. Het middenstuk is een driehoekig prisma.

De afmetingen van de zijden van zo'n driehoek zijn met behulp van de stelling van Pythagoras te berekenen.
Ga na, dat het een gelijkbenige driehoek is met benen van $sqrt(3,25)~~1,80$ m en een basis van $sqrt(2)~~1,41$ m.

Bekijk de tent in Voorbeeld. Hij heeft ook een grondzeil dat de hele bodem bedekt.

Bereken zelf de afmetingen van één van de driehoeken aan de voorkant.

De twee gelijke benen zijn $sqrt(1^2 + 1,5^2) = sqrt(3,25) ~~ 1,80$ m.
De basis is $sqrt(1^2 + 1^2) = sqrt(2) ~~ 1,41$ m.

Teken een uitslag van de tent.

Begin met het grondvlak te tekenen. Het grondvlak is een zeshoek met een maximale breedte van $4$ m en een minimale breedte van $2$ m (het middenstuk). De hoogte van het grondvlak is de breedte van de tent, dus $2$ m. Om de hoogte van de rechthoekige zijkanten en dus ook meteen de lengte van de zijden van de driehoekige grensvlakken te bepalen, moet je de lengte bepalen van de schuine zijde van de voorkant. Dit is in de figuur linksboven gedaan (rode lijnen). De lengte daarvan is ongeveer $1,8$ m. Daarna met passer vanuit de hoekpunten (delen van) cirkels maken met deze straal. Op de snijpunten komen de hoekpunten van de driehoekige grensvlakken.

Hier zie je een vereenvoudigd model van het dak van een stolpboerderij. Het dak is zuiver symmetrisch, dus de ribben $A E$ , $D E$ , $B F$ en $C F$ zijn even lang en $E F$ loopt evenwijdig met $A B$ en $C D$ .

Laat zien hoe je de figuur kunt verdelen in een prisma en twee piramides die je kunt samenvoegen tot één vierzijdige piramide. Wordt dit een regelmatige vierzijdige piramide?

Zie figuur. De piramide is niet regelmatig, want het grondvlak is geen vierkant.

Bereken de lengtes van de vier opstaande ribben van dit stolpdak.

$E P = \sqrt{5^{2} + 4^{2}} = \sqrt{41}$ en dus is $A E = \sqrt{41 + 3^{2}} = \sqrt{50}$ . Zo lang zijn alle opstaande ribben.

Bereken de drie hoeken van elk van de twee driehoekige dakdelen.

Neem aan, dat $M$ het midden van $B C$ is, dan is $M F = \sqrt{5^{2} + 3^{2}} = \sqrt{34}$ .

Dus is $tan(/_ MBF) = (sqrt(34))/4$ zodat $/_ MBF ~~ 56^@$ .
De gevraagde hoeken zijn daarom $56^@$ , $56^@$ en $68^@$ .

Bereken de vier hoeken van elk van de twee trapeziumvormige dakdelen.

$tan(/_ PAE) = (sqrt(41))/3$ zodat $/_ PAE ~~ 58^@$ .
De gevraagde hoeken zijn daarom $58^@$ , $58^@$ en $122^@$ .

Een verpakking is vaak een hol lichaam dat in zijn vorm wordt gevouwen vanuit een uitslag. (Meestal is het meer een bouwplaat, een uitslag met plakranden en allerlei extra's om de vorm stevig te houden.)

Hoe ziet een uitslag van een cilindrisch blik met een diameter van $8,6$ cm en een hoogte van $8,6$ cm er uit?

Als een rechthoek met een lengte die net zo groot is als de omtrek van de grondcirkel en een breedte van $8,6$ cm. Daar zitten dan twee cirkels met een diameter van $8,6$ cm aan vast, eentje aan de bovenkant en eentje aan de onderkant.

Teken de uitslag van de cilinder beschreven in Voorbeeld op schaal $1:2$ .

Bereken eerst de omtrek van de grondcirkel $pi*8,6~~27,0$ cm.
Maak dan de figuur zoals die in het voorbeeld, maar nu correct op schaal.

Uit een plaat koper is een halve cirkel gesneden met een diameter van $12$ cm.
Deze plaat koper wordt tot een kegelvorm gebogen.
Hoe hoog wordt die kegel en welke diameter heeft het grondvlak?

Het ronde grondvlak van de kegel ontstaat uit de halve cirkelboog van plaat koper en heeft dus een omtrek van $1/2 * pi * 12 = 6pi$ cm.
De grondcirkel van de kegel heeft een diameter $d$ . En de omtrek is $pi*d = 6pi$ .
De diameter van de grondcirkel is daarom $6$ cm.

De straal van de uitgesneden halve cirkel wordt bij de kegel de lengte van een lijnstuk vanaf de top naar de grondcirkel.
Dat is de langste zijde van een rechthoekige driehoek met rechthoekszijden de hoogte van de kegel en de straal van de grondcirkel. De hoogte van de kegel wordt daarom $sqrt(6^2 - 3^2) = sqrt(27) ~~ 5,2$ cm.

Gegeven is een kubus $A B C D . E F G H$ met zijden van $4,5$ cm.

Bereken de grootte van de hoeken $H B D$ en $F C A$ .

Teken de kubus.

$/_ HBD$ ligt in diagonaalvlak $D B F H$ , een rechthoek van $4,5 \sqrt{2}$ bij $4,5$ . Dus is $tan(/_ HBD) = (4,5)/(sqrt(40,5))$ zodat $/_ HBD ~~ 35^@$ .

$Δ A C F$ is gelijkzijdig, dus $/_ ACF = 60^@$ .

Piramide $A B C D . T$ heeft vier gelijke opstaande ribben van $10$ cm. Het grondvlak is een rechthoek met $A B = 8$ cm en $B C = 6$ cm.

Bereken de hoogte van deze piramide.

Teken de piramide.

In het grondvlak is $A C = \sqrt{8^{2} + 6^{2}} = 10$ . Als $S$ het snijpunt is van $A C$ en $B D$ , dan is $S T$ de hoogte van de piramide. Met de stelling van Pythagoras vind je $S T = \sqrt{10^{2} - 5^{2}} = \sqrt{75}$ .

Bereken de grootte van de hoeken $A T C$ en $B A T$ .

Omdat $sin(/_ ATS) = 5/10 = 0,5$ is $/_ ATS = 30^@$ en dus $/_ ATC = 60^@$ .

$/_ BAT$ ligt in de gelijkbenige driehoek $A B T$ . Dus $cos(/_ BAT) = 4/10 = 0,4$ zodat $/_ BAT ~~ 66,4^@$ .

Balk $A B C D . D E F G$ heeft ribben $A B = 4$ , $A D = 3$ en $A E = 3$ . Punt $S$ is het snijpunt van alle lichaamsdiagonalen.

Bereken $/_ ASB$ in graden nauwkeurig.

Teken de balk.

$AC = sqrt(4^2+3^2) = 5$ en $AG = sqrt(5^2+3^2) = sqrt(34)$ .
$HB = AC = sqrt(34)$ en $AS = BS = 1/2 sqrt(34)$ .
$Delta ABS$ is gelijkbenig, dus $cos(/_ BAS) = (2)/(1/2 sqrt(34))$ zodat $/_ BAS ~~ 46,7^@$ .
De gevraagde $/_ ASB ~~ 180^@ - 2*46,7^@ ~~ 87^@$ .

Bereken $/_ ASB$ in graden nauwkeurig.

Nu gebruik je de gelijkbenige driehoek $ASC$ : $tan(/_ CAS) = (5)/(sqrt(34))$ zodat $/_ CAS ~~ 40,6^@$ .
De gevraagde $/_ ASC ~~ 180^@ - 2*40,6^@ ~~ 99^@$ .

Droste chocolaatjes worden onder andere verpakt in kartonnen doosjes zoals je die hiernaast ziet. De bodem van deze doosjes is een regelmatige achthoek met zijden van ongeveer $7,8$ cm. De hoogte van zo'n Drostedoosje is ongeveer $3,3$ cm. Nadat je alle chocolaatjes op hebt haal je het plastic waar ze in hebben gelegen uit het doosje.

Welke ruimtelijke figuur stelt het doosje bij benadering voor?

Een regelmatig achtzijdig prisma.

Hoe groot zijn de hoeken van de achthoekige bodem van zo'n doosje?

De achthoek bestaat uit acht gelijkbenige driehoeken met een tophoek van $360 ° / 8 = 45 °$ .
De hoeken van de achthoek worden gevormd door twee basishoeken en zijn daarom $135 °$ .

Hoe groot is het langste rechte staafje dat je nog op de bodem van dit doosje kunt leggen? Geef je antwoord in één decimaal nauwkeurig.

Zie figuur. $A P = 7,8 \cdot sin (67,5) \approx 7,21$ . Dus $A C \approx 14,41$ .
En daardoor is $A M^{2} + M C^{2} = 2 A M^{2} \approx {14,41}^{2}$ en dus $A M \approx \sqrt{103,86} \approx 10,19$ .
Het langste staafje op de bodem heeft een lengte van $2 \cdot A M \approx 20,38 \approx 20,4$ cm.

Hoe groot is het langste rechte staafje dat in dit doosje past?

Ongeveer $\sqrt{{20,38}^{2} + {3,3}^{2}} \approx 20,6$ cm.

Je ziet hier de uitslag van een vierzijdige piramide $A B C D . T$ met een rechthoekig grondvlak.

Hoe lang zijn de ribben van deze piramide?

$\sqrt{3^{2} + 8^{2}} = \sqrt{73}$

Hoe hoog wordt deze piramide?

$\sqrt{8^{2} - 4^{2}} = \sqrt{48}$

Je ziet hier het bovenste deel van een lantaarnpaal.
De diameter van de buis van de lantaarnpaal vlak onder de lamp is $16$ cm.
De lamp zit in een afgeknotte kegel van kunststof. Daar zit nog een smalle cilindervorm met een diameter van $60$ cm boven. De afgeknotte kegel wordt gemaakt uit een kunststofplaat in de vorm van een halve cirkel met een diameter van $120$ cm waaruit een kleinere halve cirkel met hetzelfde middelpunt is weggesneden.

Hoe groot is de diameter van die kleinere cirkel en hoe hoog is de afgeknotte kegel?

Zie figuur.

De omtrek van de onderste cirkel van de afgeknotte kegel is $pi*16$ en is ook de omtrek van de uitgesneden halve cirkel. Die moet daarom een diameter van $32$ cm hebben.
De hoogte van de afgeknotte kegel is $sqrt(44^2-22^2) ~~ 38,1$ cm.

Wenteltrap

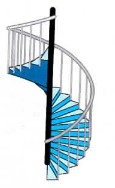
Op de wenteltrap in de figuur hiernaast maak je precies één rondgang als je naar boven gaat. De leuning zit op $1,3$ m van de as van de wenteltrap. Het hoogteverschil tussen de verdiepingen bedraagt $2,8$ m.

Bereken de lengte van de leuning.

$8,63$ m.

$AB$

$=$

$(2,6pi)$ m

$AC$

$=$

$sqrt(2,8^2+(2,6pi)^2)~~8,63$ m.

Schroefdraad

Zie de figuur.

Leg uit hoe je het aantal meter schroefdraad op een schroef kunt berekenen. Werk een voorbeeld uit.

Het aantal keren dat je de spoed op de schroef telt geeft het aantal omwentelingen. Met behulp van de stelling van Pythagoras kan je de lengte van de schroefdraad berekenen (voor de omtrek van de schroef nemen we voor het gemak dat de schroef overal even dik is).

Van een regelmatige vierzijdige piramide $T.ABCD$ is het grondvlak $ABCD$ een vierkant met zijde $4$ . $S$ is het snijpunt van de diagonalen $AC$ en $BD$ en $TS=10$ . Punt $M$ is het midden van $TS$ .

Teken deze piramide met daarin een lijn door $M$ evenwijdig aan $BD$ . Noem de snijpunten met $TB$ en $TD$ respectievelijk $P$ en $Q$ .

Bereken de lengte van $AP$ en $PQ$ .

$AP=sqrt(35)$

$PQ=sqrt(8)$

$AS=sqrt(8 )$ en $SM=5$ geeft $AM=sqrt(33 )$ .
Nu is $MP=MQ=1/2*sqrt(8 )=sqrt(2 )$ en $ΔAMP$ en $ΔAMQ$ zijn rechthoekig.
$AP=AQ=sqrt(35 )$

$PQ$ is de helft van de diagonaal in het grondvlak. Dus $PQ=sqrt(8)$ .

Teken $ΔAPQ$ op ware grootte en bereken de hoeken van deze driehoek in graden nauwkeurig.

$∠APM≈76^@$ , $∠AQM≈76^@$ en $∠PAQ≈28^@$ .

$tan(∠APM)= (sqrt(33 )) / (sqrt(2 ))$ , dus $∠APM≈76^@$ . Dit betekent dat $∠AQM≈76^@$ en $∠PAQ≈28^@$ .

Een kegel wordt gevormd uit een halve cirkel met een diameter van $40$ cm.
Hoe hoog wordt die kegel in mm nauwkeurig?

$~~ 34,6$ cm.

Omtrek grondcirkel wordt $20pi$ cm, dus diameter $20$ cm.

Dan is $h = sqrt(40^2-20^2) ~~ 34,6$ cm.