werken met de cosinusregel in (niet-rechthoekige) driehoeken.
werken met gelijkvormigheid van driehoeken en de stelling van Pythagoras toepassen;
goniometrische verhoudingen sinus, cosinus en tangens en de sinusregel toepassen;
werken met goniometrie bij hoeken die groter zijn dan .
Een regelmatige 9-hoek heeft een omgeschreven cirkel met een straal van cm.
Hoe groot is ?
Bereken de omtrek van deze 9-hoek.
is een gelijkbenige driehoek met benen van cm.
Voor de halve basis van zo'n driehoek geldt: , dus .
De omtrek is dus ongeveer cm.
Bij een crosscountry-wedstrijd moeten de deelnemers van punt naar punt zien te komen. Er zijn twee mogelijkheden. De eerste mogelijkheid is een route rechtstreeks door het bos van naar . De tweede mogelijkheid is een route via punt en een geasfalteerd fietspad. De paden en maken een hoek van met elkaar. Het pad van naar is m, dat van naar is m.
Nu is de sinusregel niet bruikbaar. Je kunt dit alleen oplossen door een hoogtelijn op te tekenen. Dat is nog behoorlijk wat rekenwerk. Handiger is het om de cosinusregel te gebruiken in .
In elke driehoek geldt:
.
In de driehoek bij de crosscountry-wedstrijd is en dus , , en .
Even invullen en je vindt m.
Bekijk in de Uitleg wat de cosinusregel is. Laat zien hoe je aan de lengte van komt met behulp van de cosinusregel.
Cosinusregel: .
Hier: .
Invullen: en m.
Bekijk driehoek . Twee zijden en de ingesloten hoek zijn gegeven.
Hoe ziet de cosinusregel bij de gegeven hoek eruit?
Bereken de derde zijde van deze driehoek.
Wil je in deze figuur uitrekenen terwijl , en bekend zijn, dan lukt dit niet met behulp van de sinusregel. Je kunt echter een verband afleiden tussen , , en .
Laat zien, dat .
Ga na, dat .
Omdat geldt: .
Laat zien dat door haakjes weg te werken.
Haakjes wegwerken: .
Verder is .
Laat tenslotte zien, dat .
Gebruik en vul dat in.
Je krijgt: .
Je kunt (door letters verwisselen) varianten op deze stelling maken, zoals en
.
In elke geldt de
Je gebruikt de cosinusregel in driehoeken die geen rechte hoek hebben en in situaties waarin de sinusregel niet goed werkt.
Bekijk de constructie van met °, en . Bereken de lengte van .
Cosinusregel: .
Dit geeft: .
Hieruit volgt: .
In het voorbeeld zie je de constructie van als gegeven is , cm en cm.
Construeer zelf deze driehoek.
Als je het goed hebt gedaan, krijg je een driehoek met dezelfde vorm en grootte als in het voorbeeld.
Controleer met de cosinusregel dat inderdaad .
.
Hieruit volgt: .
Laat zien dat de stelling van Pythagoras een speciaal geval is van de cosinusregel.
Als °, dan is de cosinusregel .
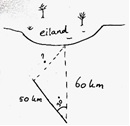
Stel je voor dat op km van een eiland je schip vergaat. Je kunt jezelf drijvend houden op een vlot, maar alle instrumenten zijn verloren gegaan. Natuurlijk probeer je rechtstreeks naar het eiland te peddelen, maar zodra je begonnen bent, komt er een dichte mist op. Je legt ongeveer km per uur af. Zonder dat je het in de gaten hebt, staat er een stroming die ervoor zorgt dat je uit de koers raakt. Na uur zou je nog km van het eiland verwijderd moeten zijn, als je er inderdaad recht naartoe gepeddeld was. Saskia maakte deze schets van de situatie.
Hoe ver ben je in werkelijkheid van het eiland af?
Noem de afstand , dan is , dit geeft km.
Noem de afstand , dan is , dit geeft km.
Van een is gegeven dat , en . Gebruik de cosinusregel om de lengte van zijde uit te rekenen.
Eerst met de sinusregel uitrekenen: geeft (de andere optie van kan niet).
geeft .
Je ziet hier twee krachten en die beide in hetzelfde punt aangrijpen.
Ze maken een gegeven hoek met elkaar.
En hun groottes zijn in N gegeven.
Bereken de grootte van de resulterende kracht .
Noem het eindpunt van punt en dat van punt .
In is
Cosinusregel: .
Dus: N.
Bekijk in
Waarom is ?
Omdat . Er zijn dus F-hoeken.
Voer zelf de berekening uit.
Zie het voorbeeld.
Bereken ook de hoek die met maakt.
Deze kun je met de sinusregel berekenen.
Met de sinusregel: .
Je vind .
Gegeven de vectoren met grootte N en met grootte N.
Ze grijpen beide aan in hetzelfde punt onder een hoek van .
is hun resultante.
Bereken de grootte van en de hoek die maakt met .
Noem het aangrijpingspunt , het eindpunt van punt en dat van punt .
In is
Cosinusregel: .
Dus: N.
De gevraagde hoek kun je met de sinusregel berekenen.
Met de sinusregel: .
Je vind .
Elke heeft zes afmetingen, te weten:
de lengtes van de zijden , en
de hoeken , en .
Hier zijn steeds drie maten van gegeven. Bereken de andere maten met de sinusregel of de cosinusregel.
, en
Met de cosinusregel vind je .
Met de cosinusregel of de sinusregel vind je nu ook dat en daarmee ook dat .
Met de cosinusregel vind je .
Met de cosinusregel of de sinusregel vind je nu ook dat en daarmee ook dat .
, en
Met de sinusregel vind je en daarmee .
Met de sinusregel of de cosinusregel vind je nu dat .
Met de sinusregel vind je en daarmee .
Met de sinusregel of de cosinusregel vind je nu dat .
, en
Met de sinusregel vind je dat .
, met de sinusregel (of de cosinusregel) vind je dat .
Met de sinusregel vind je dat .
, met de sinusregel (of de cosinusregel) vind je dat .
, en
, dus (omgekeerde stelling van Pythagoras).
Verder vind je uit dat en .
, dus (omgekeerde stelling van Pythagoras).
Verder vind je uit dat en .
en
. Met de cosinusregel, of de sinusregel, of gewoon vind je dat .
. Met de cosinusregel, of de sinusregel, of gewoon vind je dat .
Laat met een berekening zien dat een gelijkbenige driehoek met , , en onmogelijk is.
, met de cosinusregel vind je dat . Maar , dus de genoemde driehoek kan niet.
(Dit kun je ook wel op andere manieren laten zien, bijvoorbeeld dat niet klopt.)
Gegeven de vectoren met grootte N en met grootte N.
Ze grijpen beide aan in hetzelfde punt onder een hoek van .
is hun resultante.
Bereken de grootte van en de hoek die maakt met .
Noem het aangrijpingspunt , het eindpunt van punt en dat van punt .
In is
Cosinusregel: .
Dus: N.
De gevraagde hoek kun je met de sinusregel berekenen.
Met de sinusregel: .
Je vind .
Je gaat op ballonvaart. De weersvoorspelling geeft aan dat de windrichting je van punt rechtstreeks naar punt brengt. Je legt km per uur af. Zonder dat je dat weet, staat de windrichting niet zoals voorspeld, zodat je uit koers raakt. Na uur zou je nog km van punt verwijderd moeten zijn als je er inderdaad recht naartoe gezweefd was.
Hoe ver ben je er in werkelijkheid vanaf? Maak eventueel eerst een schets.
Noem het punt waar je na uur bent, punt . Na uur heb je km afgelegd, dus en .
Hiermee is . Dit geeft km.
Noem het punt waar je na uur bent, punt . Na uur heb je km afgelegd, dus en .
Hiermee is . Dit geeft km.
Je ziet hier twee tandwielen met een tussentandwiel.
Alle lengtematen zijn in mm.
Bereken de grootte van de straal van het grote tandwiel in mm nauwkeurig.
Cosinusregel:
geeft mm.
Bij allerlei constructies is de cosinusregel handig te gebruiken.
Een spant van een dakconstructie heeft de volgende afmetingen:
m, m en m.
Verder is gemeten: .
Bereken de dakhelling . Maak hierbij gebruik van de cosinusregel.
Bereken de nokhoogte .
m
Een regelmatige 9-hoek heeft een omgeschreven cirkel met een straal van cm.
Bereken de omtrek van deze 9-hoek met behulp van de cosinusregel.
is een gelijkbenige driehoek met benen van cm en een tophoek van .
Voor de basis van zo'n driehoek geldt: .
Dus is .
De omtrek is dus ongeveer cm.
Van een driehoek is gegeven , en . Bereken de lengte van in twee decimalen nauwkeurig.
geeft
Je ziet hier parallellogram met , en .
Bereken in één decimaal nauwkeurig.
geeft
Bereken de oppervlakte van het parallellogram in één decimaal nauwkeurig.
Teken hoogtelijn op .
Oppervlakte van is ongeveer