een formule opstellen van een lineaire functie waarvan de grafiek door twee gegeven punten gaat.
bij een (in woorden beschreven) lineair verband een passende formule opstellen;
het hellingsgetal (richtingscoëfficiënt) herkennen;
berekeningen met lineaire verbanden uitvoeren.
In de gemeente Overdal wordt maximaal weken per jaar het huisvuil opgehaald. In elke zwarte vuilcontainer zit een chip die er voor zorgt dat elke lediging geregistreerd wordt. De gemeente stuurt dan op het eind van het jaar een rekening. Als je iedere week de zwarte container laat legen moet je na een jaar € 381,60 betalen. Hiernaast zie je een grafiek waarin de kosten zijn uitgezet tegen het aantal weken.
Bij de grafiek hoort een formule van de vorm waarin een constante is. Waarom is dat?
De grafiek is een rechte lijn door en door . Er is daarom sprake van een recht evenredig verband.
Bereken de waarde van de evenredigheidsconstante die bij deze grafiek past.
Dit kun je bijvoorbeeld doen door en in te vullen in de formule. Je vindt
In de gemeente Vijfhouten worden de kosten voor het ophalen van de zwarte vuilcontainers anders berekend. Elk gezin betaalt per jaar € 103,20 plus een vast bedrag voor elke geleegde zwarte container. Als je iedere week de container laat legen moet je na een jaar, net als in Overdal, € 381,60 betalen.
Teken de grafiek van de jaarlijkse kosten in euro afhankelijk van het aantal weken dat de zwarte container wordt geleegd.
Zie figuur.
De grafiek is een rechte lijn, dus er hoort een formule bij van de vorm . Welke waarde heeft .
Hoe kun je de waarde van de richtingscoëfficiënt bepalen?
Je vindt (als je weet hoe) dat . Bekijk verder de Uitleg.
In de gemeente Vijfhouten worden de zwarte vuilcontainers wekelijks en maximaal keer per jaar opgehaald. Elk gezin betaalt per jaar € 103,20 plus een vast bedrag voor elke geleegde zwarte container. Als je iedere week de container laat legen moet je na een jaar € 381,60 betalen. Deze grafiek laat het verband zien tussen het aantal keren dat je de zwarte container laat legen en de kosten per jaar .
Bij deze grafiek hoort een lineaire functie van de vorm . Uit de gegevens volgt onmiddellijk . Maar hoe bepaal je nu de waarde van de richtingscoëfficiënt ?
Bekijk de twee gegeven punten van de grafiek en . Het aantal weken neemt tussen deze twee punten toe met . Het te betalen bedrag neem tussen deze twee punten toe met . Per week is dat .
De toename per eenheid is het hellingsgetal, de richtingscoëfficiënt, van de lijn.
Kortweg: .
En de bij de grafiek passende lineaire functie is .
In de Uitleg zie je hoe je het hellingsgetal berekent als je van een rechte lijn twee punten weet.
In een andere gemeente wordt hetzelfde systeem gehanteerd als in de gemeente Vijfhouten, alleen met andere bedragen. Daar betaalt de familie Arends in 2011 € 277,50 en daarvoor hebben ze de zwarte container keer laten legen. Hun buren hebben nog twee opgroeiende kinderen en moesten hun zwarte container keer laten legen. Zij betaalden dat jaar € 327,50.
Hoeveel keer extra werd de zwarte container van de buren geleegd?
keer.
Hoeveel moesten de buren meer betalen?
euro.
Hoeveel kost in deze gemeente dus het legen van de zwarte container per keer?
euro.
Ook in deze gemeente geldt een formule van de vorm .
Welke waarde heeft de richtingscoëfficiënt ?
Door welke twee punten gaat de rechte lijn die bij deze formule hoort? Hoe kun je vanuit die twee punten in één keer de richtingscoëfficiënt berekenen?
en . Hieruit vind je .
Je hebt nu gevonden dat de formule er uit ziet als . Hoe vind je de waarde van ?
Eén van de twee punten waar de grafiek door gaat is . Dus je kunt en in de formule invullen. Dan krijg je , zodat .
De grafiek van een rechte lijn gaat door en . De bijbehorende formule heeft de vorm .
Hoeveel neemt de waarde van toe tussen beide punten?
Hoeveel neemt de waarde van toe tussen beide punten?
Hoeveel neemt de waarde van toe als met wordt verhoogd?
Met .
Je hebt de waarde van de richtingscoëfficiënt berekend.
Hoe zie de formule er nu uit?
Bereken de waarde van .
Eén van de twee punten waar de grafiek door gaat is . Dus je kunt en in de formule invullen. Dan krijg je , zodat .
Schrijf tenslotte de complete formule op die bij deze lijn past.
.
Kun je je antwoord nog controleren?
Ja, op verschillende manieren. Bijvoorbeeld door na te gaan dat het andere punt ook aan de formule voldoet. En ook door de bekijken of de rechte lijn door deze twee punten wel door gaat.
De algemene formule voor een lineair verband is
met en willekeurige reële getallen.
Het
Als dan is de lijn stijgend, als dan is de lijn dalend.
Als dan is de lijn horizontaal, evenwijdig aan de -as.
Een verticale lijn heeft geen hellingsgetal.
Twee
Zijn van een lineaire grafiek alleen twee punten bekend, dan kun je zelf een bijpassende formule opstellen. Je bepaalt dan eerst het hellingsgetal van de lijn door beide punten door te berekenen hoeveel de -waarde toeneemt als de -waarde met toeneemt. (Dit kan alleen bij lijnen die niet verticaal lopen.)
Experimenteer met de applet. De punten en kun je verplaatsen. Je moet dan alleen vanuit de coördinaten van die punten de formule van de lijn door beide punten kunnen maken. Zet je de punten recht boven elkaar, dan zie je dat ook GeoGebra geen formule van de vorm kan maken...
Stel een vergelijking (formule) op bij de lijn door de punten en .
De vergelijking heeft de vorm waarin het hellingsgetal is. Dit getal vind je door te bepalen hoeveel toeneemt bij een toename van met . Dat kun je zo doen:
Tussen de punten en neemt toe met .
Tussen de punten en neemt toe met .
Als met toeneemt, neemt toe met .
Nu je weet dat het hellingsgetal , wordt je formule . De juiste waarde van bepaal je door de coördinaten van één van beide gegeven punten in de vergelijking in te vullen.
Ga na, dat je dezelfde vergelijking krijgt als in de applet. (Maar nu exact in breuken!)
Bekijk het voorbeeld en werk met de applet.
Bekijk het voorbeeld hierboven en werk met de applet.
Stel zelf de vergelijking op van de lijn door de punten en zonder het antwoord bij het voorbeeld te bekijken.
Doen. De juiste waarde van bereken je door in de formule bijvoorbeeld en (de coördinaten van punt ) in te vullen. Maar je kunt dit ook doen door met het hellingsgetal steeds door te tellen tot je op de verticale as uitkomt.
Stel een vergelijking op van de lijn door en .
Je vindt .
Stel een vergelijking op van de lijn door en .
Je vindt .
Stel een vergelijking op van de lijn door en .
Je vindt .
Stel een vergelijking op van de lijn door en .
Je vindt .
Stel een vergelijking op van de lijn door en .
Je vindt .
Bij een lineaire functie hoort bij de uitkomst en bij de uitkomst .
Stel de bijbehorende formule op.
Het hellingsgetal is , dus de formule heeft de vorm .
Vul nu de coördinaten van (bijvoorbeeld) punt in en je vindt .
De gezochte formule wordt .
Bij het
Oefen met een medeleerling.
Doen.
Als je punt recht onder punt zet, is de lijn door beide punten evenwijdig aan de -as. Welke formule hoort er bij zo'n lijn? Kun je dat verklaren?
Je vindt dan de formule omdat de lijn bestaat uit alle punten met een -waarde van . Bij zo'n soort lijn hoort geen lineaire functie, want je kunt in deze gevallen geen hellingsgetal berekenen.
Bij welke lijnen horen formules van de vorm ? Kun je dat verklaren?
Dan krijg je lijnen evenwijdig aan de -as omdat het hellingsgetal dan is.
Een lijn gaat door het punt en loopt evenwijdig met de lijn . Bij lijn hoort de formule . Welke formule hoort bij lijn ?
Omdat de lijnen en evenwijdig zijn, hebben ze dezelfde richtingscoëfficiënt. De formule bij lijn heeft dus de vorm .
De juiste waarde van bepaal je door de coördinaten van het gegeven punt van in de vergelijking in te vullen: geeft .
De gevraagde formule is .
Lijn gaat door het punt en is evenwijdig met de lijn . Bij lijn hoort de formule .
Welke formule hoort bij lijn ?
De formule bij lijn heeft de vorm . Coördinaten van het punt waar doorheen gaat invullen geeft , dus .
De gevraagde formule is .
Lijn gaat door het punt en is evenwijdig met de lijn door de punten en .
Welke formule hoort bij lijn ?
Het hellingsgetal van lijn is .
Lijn heeft dezelfde richtingscoëfficiënt, dus de formule bij lijn heeft de vorm . Coördinaten van het punt waar doorheen gaat invullen geeft , dus .
De gevraagde formule is .
De Chinese munteenheid is de yuan. Je weet wel dat er iets meer dan acht yuan in een euro gaan, maar de preciese koers schommelt nogal. Bovendien rekent een bank in China als je euro's inwisselt voor yuan waarschijnlijk nog bepaalde omrekenkosten. Op zekere dag betaal je in Beijing voor 100 yuan € 85,00 en later betaal je voor 50 yuan € 43,75. Ga er van uit dat de wisselkoers niet is veranderd intussen.
Hoeveel euro kost elke yuan?
Hoeveel bankkosten betaal je elke keer als je yuan koopt?
€ 2,50
Het bedrag in euro dat je betaalt voor yuan kun je met een lineaire formule berekenen. Ga uit van een constante wisselkoers.
Stel die formule op.
Hoeveel kosten je 250,00 yuan?
euro.
Stel in de volgende gevallen een formule op bij de beschreven lijn.
De lijn heeft een hellingsgetal van en gaat door het punt .
De lijn gaat door de punten en .
De lijn gaat door de punten en .
De lijn gaat door de punten en .
Bekijk de rechte lijnen in de grafiek. Elke rechte lijn is de grafiek van een lineaire functie.
Geef de bijbehorende formules.
Zoek op elke lijn twee punten waarvan de -waarden verschillen. Je kunt dan het hellingsgetal aflezen door vast te stellen hoeveel hun -waarden verschillen.
De tabel laat zien hoe een kaars opbrandt. Op een aantal tijdstippen is de lengte van de kaars gemeten in halve cm nauwkeurig. Teken je hierbij een grafiek dan lijken de punten op een rechte lijn te liggen. Het lijkt er daarom op dat een lineaire functie is van . Maar hoe weet je dat zeker?
| tijdstip in uur | ||||
| lengte in cm |
Neem aan dat een lineaire functie is van en stel met behulp van de eerste twee gegevens uit de tabel een daarbij passende formule op.
Je vindt .
Ga na, dat ook de andere twee gegevens in de tabel aan de gevonden formule voldoen.
Substitueer zowel en als en in de formule. In beide gevallen krijg je ware uitdrukkingen.
Waarom kun je nu wel zeggen dat de gegevens in de tabel bij een lineaire functie horen, maar kun je nog steeds niet zeggen dat een lineaire functie is van ?
Omdat je geen andere gegevens hebt weet je niet zeker wat er verder tussentijds gebeurt. En dus ook niet of de kaars voortdurend gelijkmatig opbrandt.
In een binnenvaartschip wordt grind gestort. Bij een lading van ton is de diepgang m en bij een lading van ton is de diepgang m. Bij een diepgang van m is het schip volgeladen.
De diepgang van dit schip in m is een lineaire functie van het gewicht van de lading in ton.
Stel een daarbij passende formule op.
Je vindt .
Welke diepgang heeft het lege schip?
m.
Het schip moet door een vaargeul met een diepte van m. Voor de veiligheid moet er minstens m water onder het schip overblijven.
Hoeveel ton grind mag dit schip maximaal laden? Rond je antwoord af op gehele tonnen.
Je kunt bijvoorbeeld de vergelijking oplossen. Er kan maximaal ton grind in.
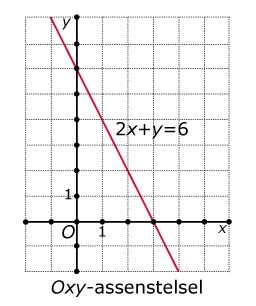
Een belangrijke toepassing van formules bij lijnen is de vlakke meetkunde. Je vat dan een lijn niet zozeer op als de grafiek van een lineaire functie, maar als meetkundig object. In dat geval moet je ook een gelijke schaalverdeling op beide coördinaatassen hebben!
Wat je in deze paragraaf hebt geleerd is het opstellen van een vergelijking van een lijn door twee gegeven punten. Daarmee kun je bijvoorbeeld nagaan of drie punten op een rechte lijn liggen, of lijnen evenwijdig zijn, of lijnen loodrecht op elkaar staan.
Hierboven kun je lezen wat de vergelijking van een lijn is.
Bekijk in
wat de vergelijking van een lijn is.
Je wilt onderzoeken of de drie punten , en op één lijn liggen.
Stel een vergelijking op van de lijn door en .
Onderzoek nu of op deze lijn ligt.
Nee, want .
Onderzoek of de punten , en op één lijn liggen.
Stel eerst een vergelijking op van een lijn door bijvoorbeeld en . Ga vervolgens na of aan die vergelijking voldoet. Dit blijkt te kloppen dus ja, deze punten liggen op één lijn.
Als van een lijn het snijpunt met de -as en het snijpunt met de -as bekend zijn, kun je snel een vergelijking opstellen.
Neem de lijn door en .
Stel een vergelijking op van de lijn door en .
Laat zien dat deze vergelijking te schrijven is als .
Doen.
Neem nu aan dat de lijn door en met zowel als ongelijk aan .
Laat zien dat de vergelijking van deze lijn te schrijven is als .
Nu moet je met letters rekenen. Eerst krijg je . En dit kun je dan herleiden tot de juiste vorm.
Van welke lijnen kun je niet een formule zoals die in c opstellen?
Van lijnen door de oorsprong en lijnen evenwijdig aan de assen.
Stel in de volgende gevallen een formule op voor de bijbehorende lineaire functie.
De grafiek is een rechte lijn door en .
De grafiek is een rechte lijn door en is evenwijdig met de rechte lijn met formule .
Het gewicht van een kabelhaspel hangt af van de lengte van de kabel die er omheen gewonden is. Zo’n grote kabelhaspel bevat nieuw wel m kabel. Hij weegt dan kg. Als er m kabel af is, weegt de haspel met kabel nog kg.
Je wilt weten hoeveel de lege kabelhaspel weegt.
Stel daartoe een formule op van de lineaire functie van het gewicht in kg afhankelijk van het aantal meter kabel op de haspel.
De grafiek van die lineaire functie gaat door en .
De bijbehorende formule is
Bereken nu hoeveel een lege kabelhaspel weegt.
Een lege kabelhaspel weegt kg.
Met deze applet kun je nieuwe lijnen maken door de punten te verplaatsen. Je kunt dan zelf de bij deze lijnen passende formules maken en deze vergelijken met de formules die de applet geeft.