het snijpunt van twee lineaire functies berekenen;

lineaire vergelijkingen en ongelijkheden oplossen.

bij een (in woorden beschreven) lineaire functie een passende formule opstellen;

het hellingsgetal (richtingscoëfficiënt) berekenen en daarmee de formule van een lineaire functie opstellen;

berekeningen met lineaire functies uitvoeren.

Je staat op een viaduct boven de snelweg. Auto $A$ rijdt er met een snelheid van $105$ km/h onder door. Auto $B$ rijdt er $5$ minuten later met een snelheid van $115$ km/h onder door.

Na hoeveel tijd heeft auto $B$ auto $A$ ingehaald?

$57,5$ minuten.

Misschien kon je bij a geen oplossing vinden, misschien ook wel.
Een aanpak van zo'n probleem is het invoeren van variabelen en het opstellen van vergelijkingen. Welke vergelijkingen bijvoorbeeld?

Noem de tijd in uur $t$ en de afstand die de auto's afleggen $a$ .
Auto $B$ rijdt op $t=0$ onder het viaduct door, dit is het startpunt $S$ . Auto $B$ is dan nog $115 * 5/60 = 115/12$ km van $S$ verwijderd.

Na $t$ uur is $A$ van $S$ verwijderd: $a = 105*t$ km.

Na $t$ uur is $B$ van $S$ verwijderd: $a = 115*t - 115/12$ km.

Beide afstanden zijn gelijk als $105*t = 115*t - 115/12$ .

Dit geeft $t = 23/24$ uur en dat is $57,5$ minuten.

Je hebt bij een bepaald probleem twee vergelijkingen gevonden zoals:
$y = text(-)x + 22$
en
$y = 2x + 4$ .

Je wilt de waarden van $x$ en misschien ook $y$ berekenen die aan beide vergelijkingen voldoen.

Je kunt daar grafieken bij tekenen zoals die hiernaast. Het punt dat aan beide formules voldoet is het snijpunt van beide grafieken. Omdat in dat punt de $y$ -waarden van beide formules gelijk zijn, kun je het uitrekenen door $- x + 22 = 2 x + 4$ op te lossen.
Deze lineaire vergelijking kun je oplossen met de balansmethode, zie Algebra 1, Vergelijkingen. Ga na dat je $x = 6$ vindt. Door invullen van deze $x$ -waarde in één van beide lineaire functies vind je ook de gewenste $y$ -waarde. Het snijpunt van beide grafieken is $(6, 16)$ .

En daarmee kun je antwoord geven op de vraag die werd gesteld.

In de Uitleg zie je hoe je het snijpunt berekent van de grafieken bij twee lineaire formules.

Bereken zelf het snijpunt van $y = text(-)x + 22$ en $y = 2x + 4$ .

Doen; ga na dat je hetzelfde antwoord krijgt als in de uitleg.

Bereken het snijpunt van de twee lijnen die horen bij de formules $y = - x + 12$ en $y = x + 13$ .

Er geldt $- x + 12 = x + 13$ oplossen. Dit geeft $2 x = - 1$ en dus $x = - 0,5$ .
Het snijpunt is $(- 0,5; 12,5)$ .

Bereken het snijpunt van de twee lijnen die horen bij de formules $y = 6 x - 1$ en $y = 3 x + 3$ .

$6 x - 1 = 3 x + 3$ oplossen geeft $3 x = 4$ en dus $x = \frac{4}{3}$ .
Het snijpunt is $(\frac{4}{3}, 7)$ .

Bereken het snijpunt van de twee lijnen die horen bij de formules $y = 2 x$ en $y = 3$ .

$2 x = 3$ oplossen geeft $x = 1,5$ .
Het snijpunt is $(1,5; 3)$ .

Je wilt het volgende probleem oplossen.

De afstand van Deventer naar Amersfoort over de snelweg A1 is $70$ km.
De éne automobilist rijdt met een constante snelheid van $100$ km/uur van Amersfoort naar Deventer. Een andere automobilist start op hetzelfde moment in Deventer en rijdt $120$ km/uur.
Op welke afstand vanaf Amersfoort gerekend, passeren ze elkaar?

Probeer het probleem op te lossen.

Eigen antwoord. Ook als het je niet lukt kun je de rest van de opgave maken.

Je kunt dit probleem oplossen met een lineaire vergelijking. Noem de tijd die ze onderweg zijn $t$ uur en de afstand tot Amersfoort die ze hebben afgelegd $s$ km.

Welke twee lineaire formules kun je opstellen?

$s = 100*t$ en $s = 70 - 120t$ .

Los het probleem verder op.

$100t = 70 - 120t$ geeft $220t = 70$ en dus $t = 70/220 ~~ 0,32$ uur.
Daarbij hoort $s ~~ 100*0,32 = 32$ km.

Als je een probleem kunt vertalen naar lineaire formules dan zeg je wel dat je een lineair model hebt gemaakt. Vaak gaat het dan om het berekenen van een snijpunt van de grafieken bij twee formules.
Het snijpunt van de grafieken bij lineaire formules zoals $y = text(-)x + 12$ en $y = 2x - 7,5$ is als volgt uit te rekenen:

Je stelt beide formules aan elkaar gelijk: $- x + 12 = 2 x - 7,5$ .

Deze lineaire vergelijking los je op met de balansmethode. Je vindt: $x = 6,5$ .

De bijbehorende waarde van $y$ vind je door de gevonden $x$ -waarde in één van beide formules te substitueren.

Je krijgt als snijpunt van beide lijnen $(6,5; 5,5)$ .

Ook een nulpunt, dus het snijpunt van de grafiek met de $x$ as, van een lineaire formule is op te sporen door een vergelijking op te lossen. Het nulpunt van de formule $y = 2 x - 7,5$ vind je door $2 x - 7,5 = 0$ op te lossen. Dit geeft $x = 3,75$ , dus het nulpunt is $(3,75; 0)$ .

Bereken het snijpunt van de lijn $l$ door $(2, 0)$ en $(3, 4)$ en de lijn $k$ door $(2, 1)$ en $(4, 0)$ .

Stel eerst bijbehorende lineaire formules op.

Bij lijn $l$ vind je de formule $y = 4 x - 8$ .

Bij lijn $k$ vind je de formule $y = - 0,5 x + 2$ .

Voor het snijpunt geldt $4 x - 8 = - 0,5 x + 2$ .

Met de balansmethode vind je $x = \frac{20}{9}$ . Het snijpunt wordt na invullen van deze $x$ -waarde $(\frac{20}{9}, \frac{8}{9})$ .

In de Theorie kun je nalezen hoe je het snijpunt van de grafieken van twee lineaire formules berekent. Ook wordt besproken wat het nulpunt van een lineaire functie is en hoe je dit berekent.

Bekijk in Voorbeeld hoe het snijpunt van twee lineaire functies wordt berekend. Voer zelf de complete berekening uit en ga na, dat je hetzelfde krijgt.

Doen.

Bereken het snijpunt van de lijn $l$ door $(0, 5)$ en $(6, 2)$ en de lijn $k$ met bijbehorende formule $y = 0,4x - 2$ .

De lineaire formule bij lijn $l$ is $y = - 0,5 x + 5$ .
Het snijpunt vind je uit $- 0,5 x + 5 = 0,4 x - 2$ .
Het snijpunt wordt $(\frac{70}{9}, \frac{10}{9})$ .

Bereken het snijpunt van de lijn $l$ door $(0, 0)$ en $(2, 1)$ en de lijn $m$ door $(0, 4)$ en $(4, 0)$ .

$l : y = 0,5 x$ en $m : y = - x + 4$ .
Voor het snijpunt is $0,5 x = - x + 4$ .
Je vindt $(\frac{8}{3}, \frac{4}{3})$ .

Twee kaarsen branden gelijkmatig op, hun lengte $L$ in cm is een lineaire functie van de brandtijd $t$ in uren. Op $t = 0$ heeft kaars I een lengte van $35$ cm en kaars II een lengte van $42$ cm. $8$ uur later zijn beide kaarsen nog $20$ cm lang.

Hoeveel tijdsverschil zit er tussen de tijdstippen waarop deze kaarsen zijn opgebrand? Geef je antwoord in minuten nauwkeurig.

Voor kaars I geldt: $L = 35 - 1,875 t$ .
Voor kaars II geldt: $L = 42 - 2,75 t$ .
Het gaat nu om de nulpunten van de grafieken bij deze formules.
Voor kaars I levert $35 - 1,875 t = 0$ op: $t = 18 \frac{2}{3}$ .
Voor kaars II levert $42 - 2,75 t = 0$ op: $t = 15 \frac{3}{11}$ .
Reken na dat het tijdsverschil ongeveer $3$ uur en $24$ minuten is.

Een goed voorbeeld van het werken met een lineair model is de keuze tussen een auto met een benzinemotor of een dieselmotor. Dat komt omdat er sprake is van twee soorten kosten per jaar, namelijk vaste kosten (voor het kopen van de auto, de verzekering en de wegenbelasting en het onderhoud) en brandstofkosten afhankelijk van het aantal gereden km per jaar.
Iemand maakt de volgende schatting:

Rijden in een benzineauto kost ongeveer 3000 per jaar en dan heb je nog jaarlijks de verzekering en de wegenbelasting, samen zo'n 500 per jaar. De brandstofkosten zijn ongeveer 1,80 per liter en je rijdt ongeveer $1$ op $12$ , dus met $1$ liter benzine rijdt je $12$ km.

Rijden in een dieselauto kost ongeveer 4000 per jaar en dan heb je nog jaarlijks de verzekering en de wegenbelasting, samen zo'n 750 per jaar. De brandstofkosten zijn ongeveer 1,20 per liter en je rijdt ongeveer $1$ op $20$ , dus met $1$ liter diesel rijdt je $20$ km.

Hierbij kan hij twee formules opstellen voor de kosten $K$ als functie van het aantal jaarlijks gereden kilometers $a$ . Laat zien hoe dat gaat en bereken bij welk aantal gereden km per jaar het rijden op diesel voordeliger is.

Leidt zelf af dat uit de gegevens volgt:

Voor de benzineauto: $K = 3500 + 0,15 a$ .

Voor de dieselauto: $K = 4750 + 0,06 a$ .

Je kunt nu narekenen dat je volgens deze schatting bij ongeveer $13900$ km per jaar voordeliger uit bent met het rijden op diesel.

In Voorbeeld zie je hoe iemand een lineair model opstelt bij de vraag wat voordeliger is, rijden op benzine of op diesel.

Laat zien hoe je uit zijn aannames de formule voor de jaarlijkse kosten van de benzineauto kunt afleiden.

De vaste kosten bedragen $3000 + 500 = 3500$ euro.
De kosten per gereden km bedragen $1,80 // 12 = 0,15$ euro.

Doe hetzelfde voor de jaarlijkse kosten van de dieselauto.

De vaste kosten bedragen $4000 + 750 = 4750$ euro.
De kosten per gereden km bedragen $1,20 // 20 = 0,06$ euro.

Bereken bij welk aantal jaarlijks gereden km de kosten voor de benzineauto even hoog zijn als voor de dieselauto. Laat zien dat het antwoord overeen komt met dat in het voorbeeld.

$3500 + 0,15 a = 4750 + 0,06 a$ oplossen geeft $a ~~ 13889$ km. En dus ben je inderdaad vanaf ongeveer $13900$ km voordeliger uit met een dieselauto.

Als een ondernemer een nieuw product op de markt brengt, dan maakt hij kosten. Die kosten kun je vaak grofweg in twee categorieën verdelen:

vaste kosten voor het ontwikkelen van het product en het opzetten van een productielijn en een magazijn;

variabele kosten die afhangen van het aantal van die producten dat hij maakt, bijvoorbeeld materiaalkosten, loonkosten, en dergelijke.

Stel je voor dat een bedrijf een nieuwe lamp op de markt wil brengen. De vaste kosten zijn becijferd op 350.000. De kosten per geproduceerde lamp bedragen 6,50. Het bedrijf gaat deze lampen verkopen voor 11,50 per stuk.

Noem het aantal verkochte lampen $q$ . Welke formule kun je dan opstellen voor de totale kosten $T K$ ?

$T K = 350000 + 6,50 q$

Welke formule kun je opstellen voor de totale opbrengst $T O$ ?

$T O = 11,50 q$

Bij beide formules horen rechte lijnen. Het snijpunt van deze twee lijnen noemen economen wel het break-even point. Bereken dit punt. Waarom heeft het die naam?

Je vindt $(70000, 805000)$ . Dit is het punt waarop het bedrijf uit de kosten gaat komen, vandaar de naam. Als er meer dan $70000$ van die lampen worden verkocht, maken ze winst.

Voor een muziekuitvoering zijn $300$ kaartjes verkocht. Kinderen betalen 2,00 en volwassenen 3,00. De totale inkomsten zijn in totaal 787,00.

Noem het aantal kinderen $k$ en het aantal volwassenen $v$ . Welke twee lineaire formules kun je dan afleiden?

$v + k = 300$ en $3 v + 2 k = 787$ .

Schrijf deze formules zo, dat $k$ een functie is van $v$ .

$k = - v + 300$ en $k = - 1,5 v + 393,5$ .

Bij beide lineaire functies horen rechte lijnen. Bereken het snijpunt van deze twee lijnen.

$- v + 300 = - 1,5 v + 393,5$ oplossen geeft $v = 187$ . Het gevraagde snijpunt is $(187, 113)$ .

Hoeveel kaartjes van elke soort zijn er verkocht?

$187$ kaartjes voor volwassenen en $113$ kinderkaartjes.

Gegeven zijn de lineaire functies $y_{1} = \frac{1}{4} x$ en $y_{2} = 2 x + 5$ .

Teken de grafieken van beide functies in één figuur en geef daarin het snijpunt en alle nulpunten aan.

Doen. De grafiek van $y_{1}$ gaat door $(0, 0)$ (en dit is ook gelijk het nulpunt) en $(4, 1)$ . De grafiek van $y_{2}$ gaat door $(0, 5)$ en $(- 2,5; 0)$ (en dit is ook gelijk het nulpunt).

Bereken het exacte snijpunt van beide grafieken.

$\frac{1}{4} x = 2 x + 5$ geeft $x = - \frac{20}{7}$ . Het snijpunt is $(- \frac{20}{7}; - \frac{5}{9})$ .

De lijn $k$ gaat door $(5, 0)$ en $(1, 1)$ . De lijn $l$ gaat door $(0, 5)$ en $(3, 0)$ .

Stel bij deze lijnen passende lineaire formules op.

$y_{1} = - 0,25 x + 1,25$ en $y_{2} = - \frac{5}{3} x + 5$ .

Bereken het exacte snijpunt van beide lijnen.

$- 0,25 x + 1,25 = - \frac{5}{3} x + 5$ geeft $- 3 x + 15 = - 20 x + 60$ en dus $x = \frac{45}{17}$ . Het snijpunt is $(\frac{45}{17}, \frac{10}{17})$ .

Een bedrijf brengt een nieuwe keukenmachine op de markt. Deze keukenmachine gaat 124,50 kosten. Om het apparaat te kunnen produceren heeft het bedrijf kosten gemaakt. Het ontwikkelen van het apparaat en het inrichten van een productielijn hebben 310.000,00 gekost. Verder kost elk apparaat het bedrijf aan materiaal en loonkosten 82,00.

Stel een formule op voor de totale kosten $T K$ voor de productie van $x$ van die keukenmachines.

$T K = 310000 + 82 x$

Stel ook een formule op voor de totale opbrengst $T O$ van de verkoop van $x$ van die keukenmachines.

$T O = 124,5 x$

Hoeveel keukenmachines moet het bedrijf minstens verkopen om winst te kunnen maken?

$310000 + 82 x = 124,5 x$ levert op $x ~~ 7294,1$ . Er moeten dus minstens $7295$ keukenmachines worden verkocht.

Een vrachtauto weegt volgeladen met $6,5$ m3 zand $14,5$ ton. Nadat de chauffeur $2,5$ m3 zand heeft bezorgd, weegt de vrachtauto met zand nog $10,75$ ton.

Hoeveel weegt de lege vrachtauto?

Noem $G$ het totale gewicht van de vrachtauto met $x$ m3 zand. Dan is de bijbehorende formule $G = 1,5 x + 4,75$ . (Formule bij een lijn door twee punten.)
De vrachtauto weegt leeg dus $4,75$ ton.

Een zebra ziet op $150$ m afstand een cheetah (jachtluipaard) en vlucht met een topsnelheid van $72$ km/h.
De cheetah zet de achtervolging in met zijn topsnelheid van $108$ km/h.

Welke twee formules voor de afstand $s$ (in m) afhankelijk van de tijd $t$ (in s) kun je dan afleiden?

Eerst omrekenen van km/h naar m/s: de cheetah rent met $30$ m/s en de zebra met $20$ m/s.

Zebra: $s = 150 + 20t$ en cheetah $s = 30t$ .

Bereken nu met behulp van de twee gevonden formules na hoeveel tijd de cheetah de zebra heeft ingehaald.

$150+20t = 30t$ geeft $t = 15$ s.

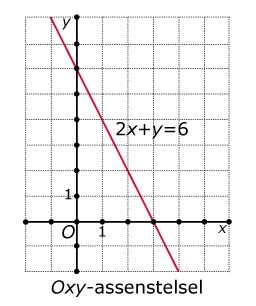
Een belangrijke toepassing van formules bij lijnen is de vlakke meetkunde. Je vat dan een lijn niet zozeer op als de grafiek van een lineaire functie, maar als meetkundig object. In dat geval moet je ook een gelijke schaalverdeling op beide coördinaatassen hebben!

Wat je in deze paragraaf hebt geleerd is het berekenen van snijpunten van lijnen. En je kunt al vergelijkingen van lijnen opstellen. Daarmee kun je bijvoorbeeld nagaan of lijnen door hetzelfde punt gaan, of punten op dezelfde lijn liggen, of lijnen evenwijdig zijn of loodrecht op elkaar staan.

Ontbrekend roosterhokje

Hierboven zie je nog eens hoe je lijnen in het platte vlak kunt beschrijven met vergelijkingen.

Bekijk in

Toepassen

hoe je lijnen in het platte vlak kunt beschrijven met vergelijkingen.

Hier zie je een klassieke puzzel waarbij kennis van lijnen en hun hellingsgetallen handig kan zijn. Bekijk de figuren I en II. Ze lijken te zijn samengesteld uit dezelfde vier rechthoekige driehoeken en twee rechthoeken. Toch is de oppervlakte van de figuur I gelijk aan $169$ en die van figuur II gelijk aan $168$ . Hoe kan dat?

Controleer eerst dat de beide gegeven oppervlaktes inderdaad kloppen.

Doen.

En, weet je waar de fout zit?

De twee grootste rechthoekige driehoeken in figuur II zijn helemaal geen driehoeken, maar vierhoeken. Er zit een knikje in wat ogenschijnlijk de schuine zijde is. Dat kun je laten zien met behulp van hellingsgetallen. Kijk in figuur II maar eens naar de grote rechthoekige driehoek linksonder. Tot het hoekpunt van de rechthoek is de helling van de schuine zijde $\frac{3}{8} = 0,375$ , daarna $\frac{2}{5} = 0,4$ .

Door één punt?

Onderzoek of deze drie lijnen door één punt gaan:

Lijn $k$ door $(0, 0)$ en $(5, 3)$ .

Lijn $l$ door $(0, 6)$ en $(11, 12)$ .

Lijn $m$ door $(- 7, - 6)$ en $(6, 2)$ .

Stel eerst van elke lijn een vergelijking op. Neem de twee eenvoudigste vergelijkingen om het snijpunt van die twee lijnen te berekenen. Controleer dat dit snijpunt ook op de derde lijn ligt. Ze gaan alle drie door $(110, 66)$ .

Je ziet hier twee rechte lijnen. Lijn $l$ is de grafiek van de lineaire functie $y = 2 x - 2$ .

Van lijn $m$ zijn twee roosterpunten gegeven. Van welke lineaire functie is deze lijn de grafiek?

De twee roosterpunten zijn $(- 2, 6)$ en $(5, 2)$ . Het hellingsgetal van de lijn $m$ wordt daarom $\frac{2 - 6}{5 - - 2} = - \frac{4}{7}$ .
Je krijgt dan een formule van de vorm $y = - \frac{4}{7} x + b$ .
Nog even de coördinaten van één van beide punten invullen en je kunt $b$ berekenen. De gevraagde lineaire functie wordt $y = - \frac{4}{7} x + \frac{34}{7}$ .

Bereken het snijpunt $S$ van beide lijnen.

Los op $2x - 2 = text(-)4/7 x + 34/7$ .
Beide zijden met $7$ vermenigvuldigen en je krijgt $14x - 14 = text(-)4x + 34$ en dus $18x = 48$ zodat $x = 24/9 = 8/3$ . Het snijpunt is $S(8/3, 10/3)$ .

Bereken het exacte nulpunt van de grafiek $m$ .

$- \frac{4}{7} x + \frac{34}{7} = 0$ geeft $x = \frac{34}{4} = 8,5$ . Het nulpunt is $(8,5; 0)$ .

Stel een formule op voor de lijn die evenwijdig loopt met $l$ en door het punt $(5, 2)$ gaat.

Het hellingsgetal van deze lijn is hetzelfde als dat van lijn $l$ . De formule heeft dus de vorm $y = 2 x + b$ . Nog even de coördinaten van het gegeven punt invullen en je vindt $y = 2 x - 8$ .

Een autoverhuurbedrijf verhuurt een Toyota voor € 75,00 per week. De benzinekosten worden geschat op € 0,12 per kilometer. Het bedrijf verhuurt ook een Renault voor € 100,00 per week. De benzinekosten van de Renault zijn ongeveer € 0,10 per kilometer.

Je wilt de Toyota voor een week huren en je hebt € 125,00. Hoeveel kilometer kun je dan rijden? Beantwoord dezelfde vraag voor de Renault.

Met de Toyota $416$ km en met de Renault $250$ km.

Toyota: 50 euro voor benzine; $50/(0,12) ≈ 416,7$ km.

Renault: 25 euro voor benzine; $25/(0,10) = 250$ km.

Geef formules voor de kosten per week van de Toyota en de Renault, afhankelijk van het aantal gereden kilometers.

$K_T = 75 + 0,12 a$ en $K_R = 100 + 0,10 a$

$a$ is het aantal kilometer, $K$ zijn de kosten in euro;

$K_T = 75 + 0,12 a$ ;

$K_R = 100 + 0,10 a$ .

Bereken vanaf welk aantal kilometer de Renault goedkoper is.

De Renault is goedkoper bij meer dan $1250$ km.

$75 + 0,12 a$

$=$

$100 + 0,10 a$

$0,02 a$

$=$

$25$

$a$

$=$

$1250$

Dus de Renault is goedkoper bij meer dan $1250$ km.