werken met machtsfuncties met negatieve exponenten;
breuken weergeven als machten en omgekeerd machten met een negatieve exponent schrijven als breuken;
de rekenregels voor machten uitbreiden met negatieve exponenten.
werken met lineaire, kwadratische functies en machtsfuncties met positieve exponent;
de rekenregels voor machten gebruiken, inclusief die voor gebroken exponenten;
tabellen maken en grafieken tekenen bij formules van twee variabelen.
Je ziet hier hoe een kegelvormige lamp een cirkelvormig lichtschijnsel op een tafel werpt. De straal van deze cirkel is recht evenredig met de hoogte van de lichtbron boven de tafel.
Waarom kun je zeggen dat de straal van deze cirkel recht evenredig is met ?
In de figuur zie je dat , dus , waarin een constante is.
De hoeveelheid licht die de lamp per seconde uitstraalt heet de lichtstroom en wordt uitgedrukt in lumen, in lm. De verlichtingssterkte op een oppervlak is het aantal lumen per m
Hierin is:
de verlichtingssterkte in lux
de lichtstroom in lm (lumen)
de oppervlakte van de verlichte cirkel in m
Verder is , waarin een constante is.
Voor een bepaalde lamp geldt lm en .
Welke formule geldt voor als functie van ?
.
Wat kun je zeggen over de verlichtingssterkte als drie keer zo groot wordt?
wordt dan keer zo klein.
Waarom is nu omgekeerd evenredig met ?
Als groter wordt, wordt juist kleiner.
De hoeveelheid licht die de lamp per seconde uitstraalt heet de lichtstroom en wordt uitgedrukt in lumen, in lm. De verlichtingssterkte op een oppervlak is het aantal lumen per m
Deze eenheid heet wel lux: lux lm/m
Hierin is:
de verlichtingssterkte in lux
de lichtstroom in lm (lumen)
de oppervlakte van het verlichte deel in m
Bij een kegelvormige lamp is , waarin (in m) de hoogte van de lamp boven het verlichte oppervlak en een constante is.
Als bijvoorbeeld lm en is:
Als groter wordt, neemt juist af (omdat je dan door een groter getal deelt).
Je zegt wel dat omgekeerd evenredig is met het kwadraat van , dus met .
Bij een formule waarin de variabele (ook) in de noemer van een breuk zit heb je te maken met een gebroken functie.
Je kunt de formule echter (met de rekenregels voor machten) ook zo schrijven:
En dus is ook recht evenredig met een macht van , namelijk met .
Je kunt zo'n gebroken functie als machtsfunctie schrijven.
Bij dit soort functies heb je te maken met bijzonder gevallen: als heel groot wordt, benadert de waarde , maar kan nooit echt worden.
Bekijk in de Uitleg de formule voor de verlichtingssterkte op een tafel oppervlak. Ga uit van een lamp met een lichtstroom van lm.
Waarom is het logisch dat omgekeerd evenredig is met de oppervlakte van het gebied dat wordt verlicht?
Als twee keer zo groot wordt moet dezelfde lichtstroom zich over een twee keer zo groot oppervlak verdelen en krijgt elk deel van dit oppervlak dus nog maar de helft van de lichtstroom.
Er wordt van een kegelvormige lichtbundel uitgegaan. Dan is .
Er wordt gekozen voor . Wat zegt dit over de kegelvorm?
De straal van de kegel is dan even groot als de hoogte van de lamp.
De lamp zelf moet een kegelvorm hebben met een hoek (dat is de halve tophoek, zie de figuur in de uitleg).
Maak de grafiek van . Neem alleen positieve waarden voor .
Gebruik GeoGebra of een grafische rekenmachine.
GeoGebra via invoerbalk: Functie(y=1/(x^2),0,50).
Dit geeft de grafiek waarbij loopt van tot en met .
Bereken als m.
lm.
Bij welke waarde van is lm?
geeft en dus m.
(Eigenlijk zijn er twee antwoorden, maar negatieve hoogtes bestaan niet.)
Grafiek: m.
Herleid de formule tot is uitgedrukt in .
Laat zien dat ook hier van een machtsfunctie sprake is.
geeft en dus .
.
Beschrijf de volgende verbanden met de termen
is omgekeerd evenredig met het kwadraat van , dus met .
Machtsfunctie: .
is recht evenredig met .
is recht evenredig met .
is omgekeerd evenredig met .
Machtsfunctie:
De basisformule voor een omgekeerd evenredig verband is de functie: , waarin een willekeurig (positief) getal is.
Bekijk de grafieken van deze functie voor , en voor .
Gebruik GeoGebra.
Bij welke waarde van hebben deze functies geen uitkomst?
Wat is er dan met hun grafiek aan de hand?
Voor is er geen uitkomst, want delen door heeft geen uitkomst.
De grafieken gaan in de buurt van steeds dichter tegen de -as aan lopen.
Neem aan dat je oneindig groot (zowel positief als negatief) zou kunnen maken.
Wat is er dan met de grafiek aan de hand?
De grafieken gaan voor -waarden heel ver van af steeds dichter tegen de -as aan lopen.
Neem nu , en bekijk de grafiek voor .
Waarom zijn er nu bij negatieve waarden van geen uitkomsten?
Omdat krijg je bij negatieve -waarden geen uitkomsten.
Laat zien, dat de formules bij deze functies te schrijven zijn als .
.
Als
Je kunt hier voorbeelden van grafieken van deze functies bekijken. Daarbij is steeds een positief getal of en .
Je ziet dat de grafieken in de buurt van steeds dichter tegen de -as gaan lopen, de -as is een
Je ziet dat de grafieken voor hele grote -waarden (positief en soms ook negatief) steeds dichter tegen de -as gaan lopen, de -as is een
Vanuit dergelijke functies kun je op meerdere manieren terugrekenen:
geeft en dan delen door en de omgekeerde macht gebruiken;
geeft en dan de omgekeerde macht of de -de machtswortel gebruiken.
Afhankelijk van de waarde van heb je één of twee antwoorden.
Bij de
De afsluitdijk is km lang. Stel dat je er met een constante snelheid (in km/h) zou kunnen rijden, dan geldt voor de tijd (in uur) die je er over doet:
Laat zien, dat een machtsfunctie is van en bepaal de bij de grafiek horende asymptoten.
Bereken de snelheid die je zou moeten hebben als je er uur over doet.
is een machtsfunctie van omdat .
Bekijk voor de asymptoten indien nodig de grafiek van de gegeven functie voor -waarden vanaf .
Je ziet dat die grafiek voor -waarden in de buurt van steeds dichter bij de verticale as gaat lopen, de -as is de verticale asymptoot.
Je ziet dat die grafiek voor hele grote -waarden steeds dichter bij de horizontale as gaat lopen, de -as is de horizontale asymptoot.
Om te berekenen bij moet je oplossen: .
Dit kan met de balansmethode: en dus km/h.
Je kunt dit ook oplossen vanuit de machtsfunctie: geeft en .
Bekijk
Laat zien hoe je uit de rekenregel kunt afleiden dat .
.
Maak zelf de grafiek van de gegeven functie.
Ga na, dat de asymptoten in je grafiek zichtbaar zijn.
Gebruik GeoGebra of een grafische rekenmachine. Kies voor waarden vanaf t/m .
Hoe lang doe je over een rit over de Afsluitdijk als je constant km/h kunt rijden?
Voer je berekening uit met de gegeven formule en ook met de machtsfunctie die erbij hoort. Geef je antwoord in minuten en seconden.
uur, dus minuten en seconden.
uur, dus minuten en seconden.
Je legt de km in minuten af door met een constante snelheid te rijden.
Hoe hard heb je gereden? Laat dit zien door met beide vormen van de formule de bijbehorende vergelijking op te lossen.
geeft en dus km/h.
geeft en dus km/h.
Met behulp van de rekenregels voor machten kun je functies met breuken vaak herleiden tot machtsfuncties van de vorm . Doe dit met de functies:
Omgekeerd kun je machtsfuncties met negatieve exponenten herleiden tot functies met breuken en soms ook wortels. Doe dit met de functies:
Je vindt:
En omgekeerd:
In het voorbeeld zie je hoe functies met breuken kunnen worden geschreven als machtsfuncties.
Schrijf de volgende functies in de vorm .
In het voorbeeld zie je ook hoe je machtsfuncties kunt schrijven zonder gebroken en/of negatieve exponenten.
Doe dit bij de volgende functies.

De kracht die twee massa's en op elkaar uitoefenen heet de zwaartekracht. Deze kracht is vooral merkbaar als het over grote massa's gaat, zoals hemellichamen. De formule voor de zwaartekracht is
Hierin is:
de zwaartekracht (in N)
de gravitatieconstante,
m
en de massa's (in kg) van de betrokken lichamen
de afstand (in m) tussen de zwaartepunten van de betrokken lichamen
Gebruik de volgende gegevens en laat zien dat voor de aantrekkingskracht tussen de aarde en de maan.
De massa van de aarde is ongeveer kg en de diameter is ongeveer km.
De massa van de maan is ongeveer kg en de diameter is ongeveer km.
Bereken de aantrekkingskracht tussen aarde en maan op het moment dat de kleinste afstand tussen een punt op het aardoppervlak en een punt op het maanoppervlak km is.
Uit de gegevens volgt:
kg
kg
km en dat is ongeveer m
Dus .
De gevraagde aantrekkingskracht is N.
Bekijk de formule voor de aantrekkingskracht (in N) tussen twee massa's in
Leg uit, hoe je aan de waarde voor komt.
Welke aanname moet je doen?
Bij de kleinste afstand tussen een punt op aarde en een punt op de maan moet je nog de halve diameters van beide lichamen optellen, want je moet de afstand tussen beide zwaartepunten (dat zijn ongeveer de middelpunten) hebben.
Je moet aannemen dat beide lichamen een zuivere bolvorm hebben.
Voer zelf de herleiding van de algemene formule tot machtsfunctie uit.
Doe de berekeningen in het voorbeeld zelf.
De afstand van de aarde tot de maan verandert in de loop van een omwenteling van de maan om de aarde.
Bij welke afstand tussen hun middelpunten is de zwaartekracht N?
geeft en dus m en dat is ongeveer km.
Je kunt de gegeven zwaartekrachtformule ook gebruiken voor het berekenen van de kracht die de aarde op objecten op zijn oppervlakte uitoefent.
Laat zien dat voor een object met massa geldt N.
.
Schrijf de volgende functies in de vorm .
Schrijf de volgende functies zonder gebroken exponenten.
Gegeven is de machtsfunctie .
Bereken als .
Bereken voor welke waarde van geldt . Rond je antwoord af op twee decimalen.
, dus
Als de waarde van twee keer zo groot wordt, met hoeveel wordt de bijbehorende uitkomst dan vermenigvuldigd?
Als je voor in de plaats invult, krijg je .
Dus met .
Licht toe dat omgekeerd evenredig is met .
.
Welke asymptoten heeft de grafiek van deze functie?
Horizontale asymptoot is de -as.
Verticale asymptoot is de -as.
In een grootwinkelbedrijf onderzoekt de commerciële afdeling hoe de tomatenverkoop afhangt van de prijs. Iemand beweert dat dan de volgende formule geldt: . Hierin is de verkoop per dag in kg en de prijs per kg in euro.
Je ziet dat omgekeerd evenredig is met . Schrijf de formule zo, dat recht evenredig is met een macht van .
Teken de grafiek van deze machtsfunctie voor prijzen tussen € 1,00 en € 5,00 per kg. Als de prijs verdubbeld wordt, wordt de afzet dan meer of minder dan de helft?
Gebruik GeoGebra, Desmos of een grafische rekenmachine.
Bij verdubbeling van de prijs wordt de afzet gehalveerd.
Het bedrijf heeft een voorraad van kg tomaten. Bereken de prijs waarbij de voorraad binnen een dag is verkocht. Geef ook de formule waarmee je dit direct kunt berekenen.
geeft dus € 1,36 per kg tomaten.
kun je herleiden tot .
Hoe groot is de verkoop bij een prijs van € 0,01? En bij € 100,00? Geef aan wat dit betekent voor de bruikbaarheid van deze formule.
Bij € 0,01 hoort en bij € 100,00 hoort .
Dit zijn weinig realistische situaties. Sowieso heeft het bedrijf maar kg tomaten op voorraad. Dus er moet gelden dat . Dus voor € 0,01 en € 100,00 is de formule niet bruikbaar.
zijn bijvoorbeeld wel bruikbare prijzen per kg voor de tomaten.
Ga uit van een massieve ijzeren balk met twee ribben van cm en een derde ribbe van cm. De soortelijke massa van ijzer is g/cm
Laat zien, dat omgekeerd evenredig is met het kwadraat van en stel een bijpassende formule op.
, dus en .
Laat zien, dat omgekeerd evenredig is met de wortel van en stel een bijpassende formule op.
, dus en zodat .
Voor de elektrische weerstand in een draad geldt de wet van Pouillet:
Hierin is:
de weerstand in Ω (Ohm)
de lengte van de draad in m
de oppervlakte van de doorsnede in m
de soortelijke weerstand van het materiaal
In welke eenheid druk je uit?.
In Ωm
Neem aan dat de draad zuiver rond is, dan geldt , waarin de diameter (in m) van de draad is.
Verder geldt voor koper dat Ωm is.
Bereken de weerstand van een koperdraad met een diameter van mm en een lengte van m.
Nu is .
Dus Ω.
Bereken de diameter van een koperdraad met een lengte van m en een gemeten weerstand van Ω.
geeft en dus zodat m, dus is mm.
Laat voor een koperdraad met een lengte van m zien, dat .
geeft .
Waarom kun je zeggen dat recht evenredig is met de lengte en omgekeerd evenredig is met het kwadraat de diameter van de koperdraad?
dus (bijvoorbeeld) het verdubbelen van betekent ook het verdubbelen van , maar het verdubbelen van betekent het delen van de weerstand door .
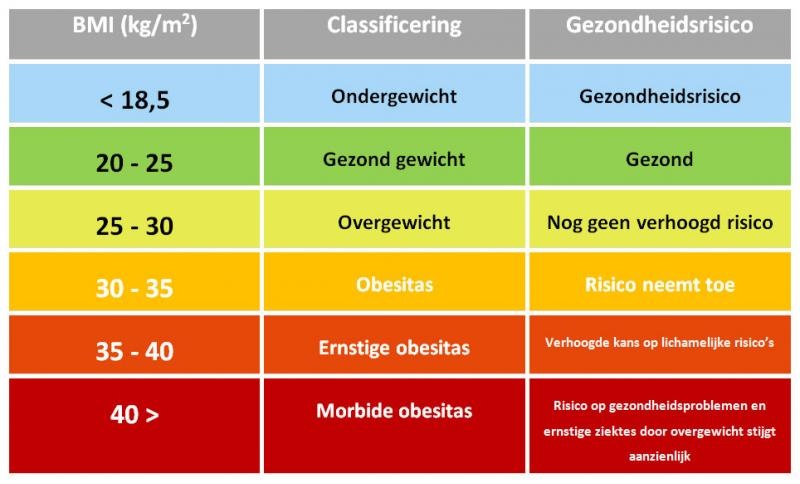
Een bekende maat voor iemands gezondheid is de
Hierin is:
het lichaamsgewicht in kilogram
de lengte in meter
de bodymass index
Bij een vanaf tot heb je een normaal lichaamsgewicht.
In de tabel vind je meer gegevens.
Bekijk de formule voor de bodymass index.
Hoe kun je aan de formule zien, dat de recht evenredig met het lichaamsgewicht (in kg) en omgekeerd evenredig met het kwadraat van de lengte (in m) is?
Als je constant houdt, ziet de formule er uit als , dus is de recht evenredig met het lichaamsgewicht.
Als je constant houdt, ziet de formule er uit als , dus is de omgekeerd evenredig met .
Bereken jouw eigen . In welke categorie val je?
Eigen antwoord.
Stel je voor dat . Welke formule geeft het verband tussen en ? Maak de grafiek van als functie van . Kies geschikte afmetingen van het assenstelsel.
, dus .
Voer in: .
Assenstelsel bijvoorbeeld: en
De grafiek wordt een rechte lijn door de oorsprong van het assenstelsel.
Stel je voor dat . Welke formule geeft het verband tussen en ? Maak de grafiek van als functie van . Kies geschikte afmetingen van het assenstelsel.
, dus .
Voer in: .
Assenstelsel bijvoorbeeld: en
Stel je voor dat . Welke formule geeft het verband tussen en ? Maak de grafiek van als functie van . Kies geschikte afmetingen van het assenstelsel.
, dus en .
Voer in:
Assenstelsel bijvoorbeeld: en
Je ziet hier de mogelijke waarden van de weergegeven in grafieken.
Hoe zien de formules bij deze grafieken er uit?
Omdat op de verticale as staat, hebben ze de gedaante
, dus zodat en .
is recht evenredig met .
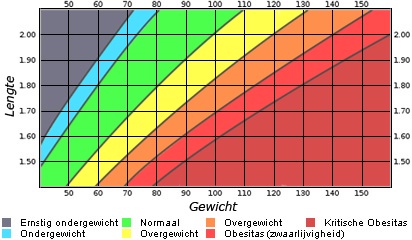
Je ziet hier een figuur waarmee je de snel kunt bepalen.
Welke heeft iemand van meter met een lichaamsgewicht van kg?
Controleer de uitkomst met de formule.
Uit het nomogram lees je af. Met de formule: . Beide waarden stemmen goed overeen. Controleer nog een paar waarden.
Hoe zwaar is iemand van m met een normaal lichaamsgewicht?
Met het nomogram: tussen en kg.
Met de formule:
Een normaal gewicht zit bij deze lengte tussen en kg.
Schrijf deze functies als machtsfuncties, dus in de vorm .
Herleid deze functies tot een vorm zonder negatieve en/of gebroken exponenten.
Het volume van een cilinder kun je berekenen met de formule . Hierin is de diameter van het grondvlak en de hoogte van de cilinder, beide in cm. Je wilt blikken maken met een inhoud van liter.
Laat zien, dat dan omgekeerd evenredig is met het kwadraat van en geef de bijbehorende formule.
.
geeft .
Herschrijf deze formule tot een formule waarin recht evenredig is met een macht van . Bepaal de evenredigheidsconstante.
de evenredigheidsconstante is
Maak een grafiek bij deze formule en bepaal de twee asymptoten.
Horizontale asymptoot: de -as.
Verticale asymptoot: de -as.
Bereken de diameter als de hoogte van deze cilinder cm is.
cm.
geeft en dus cm.