herkennen of een wortelfunctie uit een standaard machtsfunctie is ontstaan en welke transformaties daar bij horen;

herkennen of een gebroken functie uit een standaard machtsfunctie is ontstaan en welke transformaties daar bij horen.

werken met machtsfuncties met alle mogelijke exponenten en de rekenregels voor machten daarbij gebruiken;

tabellen maken en grafieken tekenen bij formules van twee variabelen;

aan een formule herkennen of de bijbehorende grafiek door transformaties uit die van een standaardfunctie kan ontstaan.

Je staat bij een uitkijktoren op een heuvel die een hoogte heeft van $25$ m boven het aardoppervlak.
Voor de afstand $a$ (in m) die je kunt kijken vanaf een ooghoogte $h$ (in m) geldt $a = 3572*sqrt(h+25)$ m.
Hierbij wordt aangenomen dat $h$ de ooghoogte boven de heuvel is.
Wil je de grafiek bij deze functie maken, dan voer je in $y = 3572*sqrt(x+25)$ .

Licht toe dat de grafiek bij deze formule kan worden afgeleid uit de grafiek van $y=x^(0,5)$ .

Je kunt de formule schrijven als $y=3572*(x+25)^(0,5)$ .

Welke transformaties moet je toepassen op de grafiek van $y=x^(0,5)$ om de grafiek bij de gegeven formule te krijgen?

Een verschuiving in de $x$ -richting met $text(-)25$ .

Een vermenigvuldiging met $3572$ in de $y$ -richting.

Je kunt in de functie $y=x^(0,5)$ geen negatieve getallen invullen, want dat is eigenlijk een wortelfunctie.

Wat betekent dit voor de waarden van $h$ die je in de formule kunt invullen?

$h ge text(-)25$

Is $a$ recht evenredig met $h^(0,5)$ ?

Nee, omdat er binnen de wortelvorm eerst nog $25$ bij $h$ moet worden opgeteld. Als $h$ twee keer zo groot wordt, wordt $a$ niet twee keer zo groot.

In een biologisch laboratorium is onderzoek gedaan naar de tijd die bij een bepaalde temperatuur nodig is om $50$ % van het zaad van een plant te laten ontkiemen. Proefondervindelijk werd dit verband tussen de tijd in dagen en de temperatuur in °C (graden Celsius) gevonden: $t = 89/(T−2)$ . Hierin is $T$ de temperatuur in °C en $t$ de tijd in dagen.
Wil je de grafiek bij deze functie maken, dan voer je in $y = 89/(x-2)$ .

Licht toe dat de grafiek bij deze formule kan worden afgeleid uit de grafiek van $y=x^(text(-)1)$ .

Je kunt de formule schrijven als $y=89*(x-2)^(text(-)1)$ .

Welke transformaties moet je toepassen op de grafiek van $y=x^(text(-)1)$ om de grafiek bij de gegeven formule te krijgen?

Een verschuiving in de $x$ -richting met $2$ .

Een vermenigvuldiging met $89$ in de $y$ -richting.

Je kunt in de functie $y=x^(text(-)1)$ niet $x=0$ invullen, want delen door $0$ levert geen reële waarde op.

Wat betekent dit voor de waarden van $T$ die je in de formule kunt invullen?

$T$ mag in ieder geval geen $2$ zijn en waarden onder de $2$ °C zijn vast ook niet bruikbaar, dus $T ge 2$ .

Is $t$ recht evenredig met $T^(text(-)1)$ ?

Nee, omdat er binnen de noemer eerst nog $2$ van $T$ moet worden afgetrokken. Als $T$ twee keer zo groot wordt, wordt $t$ niet twee keer zo groot.

Alle functies van de vorm $y=x^p$ met $p$ een willekeurig reëel getal en alle functies die daaruit door transformatie kunnen ontstaan heten machtsfuncties.

Als $p = 1/n$ met $n=2,3,4,5,...$ dan spreek je van wortelfuncties:

$a = 3572 sqrt(h+25 ) = 3572 (h+25)^(1/2)$

$y = 40 + root[3](2x) = (2x)^(1/3) + 40$

De grafieken ervan kun je door transformatie afleiden uit die van de bijbehorende machtsfunctie. Ze hebben daarom dezelfde eigenschappen.

Je kunt vergelijkingen oplossen door de omgekeerde macht te gebruiken. Je moet er dan wel eerst voor zorgen dat je de vergelijking zo schrijft dat de macht (of de wortelvorm) geïsoleerd aan één kant van het isgelijkteken en de rest aan de andere kant van het isgelijkteken staat.

Er bestaan ook functies waar wel wortelvormen in voorkomen, maar daarnaast ook andere uitdrukkingen. Een voorbeeld is de functie $y = x^2 - 3xsqrt(x)$ . Dit is geen wortelfunctie, maar je kunt de formule herleiden tot een verschil van twee machtsfuncties. Zo kun je er toch goed aan rekenen...

In Uitleg zie je dat wortelfuncties als machtsfunctie kunnen worden geschreven. Schrijf de volgende functies als machtsfunctie als dat kan.

$y = 4 sqrt(x)+3$

$y = 4 x^ (1/2) +3$

$y = sqrt(4 +x^2)$

Geen echte machtsfunctie, je kunt er wel $y = (4 + x^2)^(1/2)$ van maken.

$y = 4/(sqrt(x)) +3$

$y = 4x^(text(-)1/2) + 3$

De functie $y = text(-)3 sqrt(x - 8) + 6$ is een wortelfunctie.

Maak de grafiek van deze functie en beschrijf met welke transformaties die grafiek kan worden verkregen uit de grafiek van $y = sqrt(x) = x^(1/2)$ .

Voer $y = text(-)3 sqrt(2x - 8) + 6$ in.

De mogelijke transformaties zijn:

eerst verschuiving van $8$ naar rechts;

vervolgens vermenigvuldigen met $text(-)3$ in de $y$ -richting;

tenslotte verschuiving van $6$ omhoog.

Bereken algebraïsch het nulpunt van deze functie.
(Let er op dat je eerst de wortel isoleert.)

Schrijf $text(-)3 sqrt(x - 8) + 6 = 0$ eerst als $sqrt(x - 8) = 2$ . Daarmee heb je de wortel geïsoleerd.

Nu ga je kwadrateren en vind je $x = 12$ .

Je kunt in $y = sqrt(x) = x^(1/2)$ geen negatieve $x$ -waarden invullen.
Welke waarden kun je in de gegeven formule invullen?

$x - 8 ge 0$ betekent $x ge 8$ .

Los op: $text(-)3 sqrt(x-8 ) + 6 le text(-)12$ .

$text(-)3 sqrt(x-8 ) + 6 = text(-)12$ geeft $sqrt(x - 8) = 6$ .

Kwadrateren: $x - 8 = 36$ en dan verder oplossen. Je vindt: $x = 44$ .

De oplossing van de ongelijkheid is $8 ≤ x ≤ 44$ .

Alle functies van de vorm $y=x^p$ met $p$ een willekeurig reëel getal en alle functies die daaruit door transformatie kunnen ontstaan heten machtsfuncties.

Als $p = text(-)n$ met $n=1,2,3,4,5,...$ dan spreek je van gebroken functies:

$t = 89/(T−2) = 89*(T-2)^(text(-)1)$

$y = 15/((x-1)^2) + 40 = 15*(x-1)^(text(-)2) + 40$

De grafieken ervan kun je door transformatie afleiden uit die van de bijbehorende machtsfunctie. Ze hebben daarom dezelfde eigenschappen, zoals asymptoten die je kunt afleiden uit die van de standaard machtsfunctie.

Je kunt vergelijkingen oplossen door de omgekeerde macht te gebruiken. Je moet er dan wel eerst voor zorgen dat je de vergelijking zo schrijft dat de macht geïsoleerd aan één kant van het isgelijkteken en de rest aan de andere kant van het isgelijkteken staat.

Er bestaan ook functies waar wel breuken in voorkomen, die niet tot een machtsfunctie zijn te herleiden. Een voorbeeld is de functie $y = x^2 - 3/x$ . Soms kun je daar toch goed aan rekenen...

In Uitleg zie je dat sommige gebroken functies als machtsfunctie kunnen worden geschreven. Schrijf de volgende gebroken functies als machtsfunctie als dat kan.

$y = 1/x^2 + 4$

$y = x^(text(-)2) + 4$

$y = 1/(4 +x^2)$

Dit is geen machtsfunctie.

$y = 2/((x-3)^4) + 10$

$y = 2(x-3)^(text(-)4) + 10$

$y = (4 + x) /x$

$y = 4/x + x/x = 4/x + 1 = 4 x^(text(-)1) + 1$

Gegeven is de gebroken functie $y = 3/((x - 4)^2) + 1$ .

Uit welke standaardfunctie kan de grafiek hiervan door transformatie ontstaan?
En welke transformaties moet je dan achtereenvolgens toepassen?

Bedenk: $y = 3*(x - 4)^(text(-)2) + 1$ .

Uit de grafiek van $y = 1/(x^2) = x^(text(-)2)$ .

Je moet op die grafiek:

eerst een verschuiving van $4$ naar rechts,

vervolgens een vermenigvuldiging met $3$ in de $y$ -richting,

tenslotte een verschuiving van $1$ omhoog

toepassen.

Welke twee asymptoten heeft de grafiek van de gegeven functie?
Welke $x$ -waarde mag je er dus niet invullen?

De asymptoten van de bijbehorende standaardfunctie zijn de beide assen.
Door de transformaties wordt de verticale asymptoot $x = 4$ en de horizontale $y = 1$ .

$x=4$ mag je niet invullen.

Los op: $3/((x - 4)^2) + 1 ≥ 4$ .

$3/((x-4)^2) + 1 = 4$ geeft $3/((x-4)^2) = 3$ en dus $(x-4)^2 = 1$ .

Daaruit volgt $x-4=1 vv x-4=text(-)1$ en $x=5 vv x=3$ .

Grafiek: $3 ≤ x lt 4 vv 4 lt x ≤ 5$ .

Als een wortelfunctie kan worden geschreven als een machtsfunctie van de vorm $y=a(x+b)^(1/n) + c$ , waarin $n = 2,3,4,...$ , dan kan hij ontstaan door transformatie van $y=x^(1/n)$ .
Hij heeft dan dezelfde eigenschappen als die machtsfunctie.

Als een gebroken functie kan worden geschreven als een machtsfunctie van de vorm $y=a(x+b)^(text(-)n) + c$ , waarin $n = 1,2,3,4,...$ , dan kan hij ontstaan door transformatie van $y=x^(text(-)n)$ .
Hij heeft dan dezelfde eigenschappen als die machtsfunctie.

De trillingstijd van een trillende massa aan een veer hangt af van de veerconstante. Er geldt:

$T = 2pi sqrt(m/c)$

Hierin is:

$T$ de trillingstijd in seconden

$m$ de massa in kg

$c$ de veerconstante in N/m

Van een veer is de veerconstante bekend: $c=7,5$ N/m.
Laat zien dat $T$ een wortelfunctie is van $m$ en bereken $m$ als $T = 2$ .

$T = 2pi sqrt(m/c) = 2pi (m/(7,5))^(1/2) = (2pi)/(7,5^(1/2))*m^(1/2) ~~ 2,29*sqrt(m)$ .

Nu duidelijk is dat $T$ recht evenredig is met $sqrt(m)$ kun je er gemakkelijk mee rekenen:

$T = 2$ betekent $2,29*sqrt(m) = 2$ .

Je vindt dan $m ~~ 0,76$ kg.

Bekijk de formule in Voorbeeld.

Je ziet dat $T$ recht evenredig is met $sqrt(m)$ .
Bereken de evenredigheidsconstante in drie decimalen nauwkeurig.

Je zou $~~2,294$ moeten vinden.

Door welke transformatie kan de grafiek van $T = 2,29sqrt(m)$ uit de bijbehorende standaardfunctie ontstaan?

Door vermenigvuldiging met $2,29$ in de $T$ -richting.

Los de vergelijking $2,29*sqrt(m) = 2$ zelf op.

$2,29*sqrt(m) = 2$ geeft $sqrt(m) = 2/(2,29)$ en dus $m = (2/(2,29))^2 ~~ 0,76$ .

De formule $T = 2pi sqrt(m/c)$ kun je ook gebruiken om de veerconstante $c$ te berekenen.

Laat zien, dat je de formule kunt schrijven als $c = (4pi^2 m)/(T^2)$ .

Beide zijden van $T = 2pi sqrt(m/c)$ kwadrateren geeft $T^2 = (4pi^2 m)/c$ .

Dit wordt $c*T^2 = 4pi^2 m$ en dus $c = (4pi^2 m)/(T^2)$ .

Hoe groot is de veerconstante als een gewicht van $1$ kg een trillingstijd van $2$ s oplevert?

$c = (4pi^2 * 1)/(2^2) ~~ 9,87$ N/m.

Een school heeft een kopieerapparaat voor zijn studenten waarmee ook in kleur kan worden afgedrukt. De jaarlijkse huur (inclusief onderhoud) van dit apparaat bedraag 840,= en elke kleurenkopie kost de school 0,45.

De studenten moeten per kopie 0,60 betalen.

Om te berekenen bij hoeveel kopieën per jaar de school uit de kosten komt, maakt een administrateur een formule voor de kosten $k$ per kopie, afhankelijk van het aantal kopieën $a$ .
Stel zelf zo'n formule op en laat zien dat $k$ een getransformeerde machtsfunctie is van $a$ .

$k = (840 + 0,45a)/a = 840/a + (0,45a)/a = 840/a + 0,45 = 840*a^(text(-)1) + 0,45$ .

De school komt uit de kosten als $840/a + 0,45 le 0,60$ .

Ga na dat dit het geval is als $a ge 5600$ .

Bekijk de formule in Voorbeeld.

Je ziet dat $k$ een getransformeerde machtsfunctie is van $a$ .

Door welke transformatie kan de grafiek van $k = 840*a^(text(-)1) + 0,45$ uit de bijbehorende standaardfunctie ontstaan?

Door vermenigvuldiging met $840$ en verschuiving van $0,45$ in de $k$ -richting.

Welke twee asymptoten heeft de grafiek van $k$ ?

Verticale asymptoot $a=0$ .

Horizontale asymptoot $k=0,45$ .

Los de ongelijkheid $840/a + 0,45 le 0,60$ zelf op.

$840/a + 0,45 = 0,60$ geeft $840/a = 0,15$ en dus $a = (840)/(0,15) = 5600$ .

Grafiek: $a ge 5600$ .

Laat zien, dat je deze functie een getransformeerde machtsfunctie is.

$t=89*(T-2)^(text(-)1)$

Welke twee asymptoten heeft de grafiek van $t$ ?

Verticale asymptoot $T=2$ .

Horizontale asymptoot $t=0$ .

Bij welke temperatuur is binnen $5$ dagen $50$ % van het zaad ontkiemt?

Je moet oplossen: $89/(T−2) le 5$ .

$89/(T−2) = 5$ geeft $T-2 = 89/5$ en dus $T = 19,8$ °C.

Grafiek: $T ge 19,8$ °C.

Gegeven is de functie $y = 40 - 10sqrt(x+12)$ .

Laat zien dat dit een getransformeerde machtsfunctie is.

$y = text(-)10*(x+12)^(1/2) + 40$ .

Benoem de transformaties die nodig zijn om de grafiek van deze functie uit de bijbehorende standaardfunctie af te leiden.

Eerst verschuiven met $text(-)12$ in de $x$ -richting, dan vermenigvuldigen met $text(-)10$ in de $y$ -richting en tenslotte $40$ omhoog verschuiven.

Welke waarden van $x$ kun je in deze functie invullen?

Er moet gelden $x+12 ge 0$ en dus $x ge text(-)12$ .

Bepaal de snijpunten van de grafiek van de gegeven functie met de beide assen.

Snijpunt met de $y$ -as: $x=0$ geeft $y=40-10sqrt(12)~~5,36$ .
Het punt is $(0; 5,36)$ .

Snijpunt met de $x$ -as: $y=0$ geeft $40 - 10sqrt(x+12)=0$ .

Dit wordt $sqrt(x+12)=4$ en $x+12=16$ , dus $x=4$ . Controleren: het klopt.
Het punt is $(4, 0)$ .

Los algebraïsch op: $40 - 10sqrt(x+12) ge 10$ .

$40 - 10sqrt(x+12) = 10$ geeft $sqrt(x+12) = 3$ .

Kwadrateren geeft $x+12=9$ en dus $x = text(-)3$ .

Grafiek: $text(-)12 le x le text(-)3$ .

Gegeven de functie $y = 40 -100/((x+10)^3)$ .

Laat zien dat dit een getransformeerde machtsfunctie is.

$y = text(-)100 (x+10 ) ^(text(-)3)+40$

Bepaal de asymptoten van de grafiek van de gegeven functie.

De grafiek onstaat door die van $y = 1/(x^3)$ met $text(-)10$ in de $x$ -richting te verschuiven, dan met $text(-)100$ in de $y$ -richting te vermenigvuldigen en tenslotte met $40$ in de $y$ -richting te verschuiven. De asymptoten verschuiven mee.

Verticale asymptoot $x=text(-)10$ en horizontale $y=40$ .

Bereken het nulpunt van de grafiek van de gegeven functie.

$100/((x+10)^3)=40$ geeft $(x+10) ^3=2 1/2$ en dus $x=text(-)10 +root[3](2 1/2) ~~ text(-)8,64$ .
Het nulpunt is $(text(-)8,64; 0)$ .

Fruittelers bespuiten hun bomen regelmatig met insecticiden, stoffen om insecten die schadelijk zijn voor hun fruit te bestrijden. De opbrengst $P$ (in kg) per appelboom hangt af van de hoeveelheid insecticide $a$ (in liter) volgens de formule:

$P = 160 - 65/(1+a)$

Hier is $a le 0 le 10$ .

Hoeveel bedraagt de opbrengst per appelboom als er geen insecticide wordt gespoten?

$P=160-65/1 = 95$ kg.

Welke asymptoten heeft de grafiek van $P$ als functie van $a$ ?
Licht je antwoord toe met behulp van transformaties.

De grafiek onstaat door die van $P = 1/a$ met $text(-)1$ in de $a$ -richting te verschuiven, dan met $text(-)65$ in de $P$ -richting te vermenigvuldigen en tenslotte met $160$ in de $P$ -richting te verschuiven. De asymptoten verschuiven mee.

Verticale asymptoot $a = text(-)1$ (heeft eigenlijk geen betekenis).

Horizontale asymptoot $P = 160$ .

Hoeveel liter insecticide moet er worden gespoten om de opbrengst per appelboom hoger dan $140$ kg te laten zijn?

Los op $160 - 65/(1+a) ge 140$ .

$160 - 65/(1+a) = 140$ geeft $65/(1+a)=20$ en dus $1+a=65/20$ zodat $a = 2,25$ L.

Grafiek: $a gt 2,25$ L.

De bovenzijde van deze poort heet wel een tudorboog.

Neem aan dat de $y$ -as door het midden van de poort loopt, evenwijdig aan de opstaande zijden. Neem ook aan dat de $x$ -as loopt door de twee onderste punten van de boog. Dan geldt voor de rechterkant van een bepaalde tudorboog de formule:

$y = sqrt(3-2x)$

Hierin is:

$x$ de horizontale afstand van een punt van de boog tot het midden ervan in m

$y$ de verticale afstand van een punt van de boog tot de $x$ -as in m

Voor deze formule geldt $0 le x le 1,5$ .

Verder is het linkerdeel van de boog het spiegelbeeld van het rechterdeel.

Maak een schets van de tudorboog met behulp van een grafiek van de gegeven formule.
Welke formule geldt voor het linkerdeel van de tudorboog?

Zie de figuur.
Voor het linkerdeel geldt $y = sqrt(3-2*(text(-)x)) = sqrt(3+2x)$ .

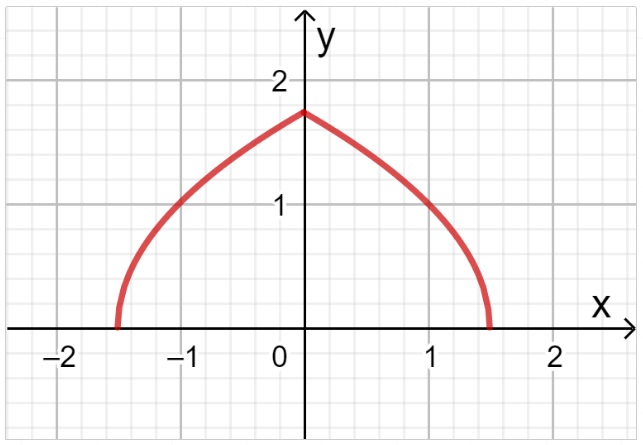
Zie de figuur.

Bereken hoe hoog het hoogste punt van de tudorboog boven de $x$ -as zit.

Neem $x=0$ en je vindt $y = sqrt(3) ~~ 1,73$ m.

Hoe groot is de afstand tussen de twee punten van de boog die $1$ m boven de $x$ -as zitten?

$sqrt(3-2x)=1$ geeft $3-2x = 1$ en dus $x=1$ .
Die punten liggen $2$ m van elkaar.

De kracht die twee massa's $m_1$ en $m_2$ op elkaar uitoefenen heet de zwaartekracht. Deze kracht is vooral merkbaar als het over grote massa's gaat, zoals hemellichamen. De formule voor de zwaartekracht is

$F = G * (m_1 * m_2)/(r^2)$

Hierin is:

$F$ de zwaartekracht (in N)

$G$ de gravitatieconstante, $G ~~ 6,674 xx 10^(text(-)11)$ m3s-2kg-1

$m_1$ en $m_2$ de massa's (in kg) van de betrokken lichamen

$r$ de afstand (in m) tussen de zwaartepunten van de betrokken lichamen

De massa van de maan is ongeveer $7,35*10^22$ kg en de diameter is ongeveer $3476$ km.

Je wilt de zwaartekracht van de maan berekenen van voorwerpen op of vlak boven (minder dan $10$ km hoog) het maanoppervlak.

Laat zien dat de zwaartekracht van een voorwerp met massa $1$ kg op een afstand $a$ (in m) boven het maanoppervlak wordt beschreven door de formule:

$F = (49,1*10^(11))/((a+1738000)^2)$

Je moet $r$ vervangen door $a+1738000$ en voor $g$ , $m_1$ en $m_2$ de juiste getallen invullen.
De formule wordt $F ~~ 6,674 * 10^(text(-)11) * (7,35*10^22 * 1)/((a+1738000)^2) ~~ (49,1*10^(11))/((a+1738000)^2)$ .

De grafiek van deze functie kan door transformatie ontstaan uit die van $F=a^(text(-)2)$ .
Welke transformaties moet je dan toepassen?

$F = 49,1*10^11 * (a + 1738000)^(text(-)2)$ onstaat uit $F=a^(text(-)2)$ door:

eerst verschuiving van $text(-)1738000$ in de $a$ -richting;

dan vermenigvuldiging met $49,1*10^11$ in de $F$ -richting.

Welke asymptoten heeft de grafiek van $F = (49,1*10^(11))/((a+1738000)^2)$ ?

Verticale asymptoot $a = text(-)1738000$ (heeft eigenlijk geen betekenis).

Horizontale asymptoot $F = 0$ .

Op welke hoogte boven het maanoppervlak ondervindt een voorwerp met een massa van $1$ kg een aantrekkingskracht van $1,5$ N?

$(49,1*10^(11))/((a+1738000)^2) = 1,5$ geeft $(a + 1738000)^2 = 32,7*10^11$ , dus $a~~71235$ m. Dat is op ongeveer $71,2$ km boven het maanoppervlak.

Koolmonoxide (CO) is één van de stoffen die via de uitlaat van een auto de lucht in komt. Deze figuur van de site van de ANWB laat dat zien.

Bron: ANWB

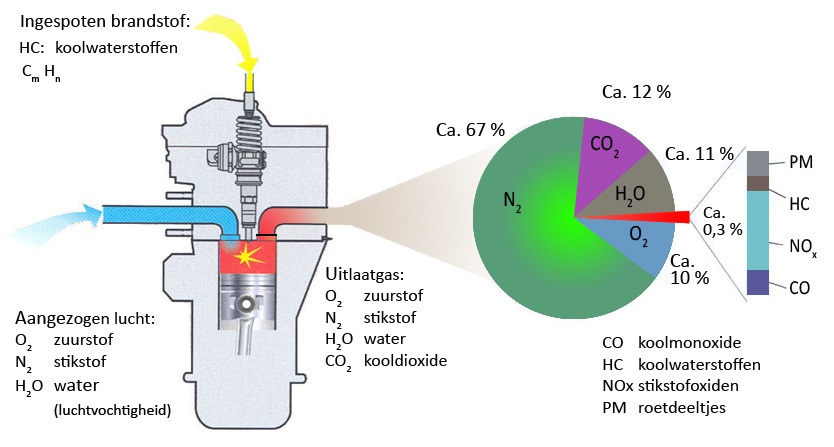
Volgens onderzoek is de hoeveelheid CO die uitgestoten wordt afhankelijk van de temperatuur van de motor en van de rijsnelheid. Voor de CO-uitstoot bij een warme motor geldt:

$u=4,4 +(196,0)/v$

Bij een koude motor geldt:

$u=6,9 +(298,5)/v$ .

Hierin is $u$ de uitstoot in gram per kilometer en $v$ de snelheid in kilometer per uur.
Deze formules zijn alleen geldig voor $v ge 10$ .

Bekijk de gegevens van CO-uitstoot bij de motor van een rijdende auto.

Hoe kun je aan de formules zien dat de uitstoot afneemt als de snelheid toeneemt?

De waarde van de breuk wordt kleiner als $v$ groter wordt.

De uitstoot van een koude motor bedroeg $14$ g/km. Hoe hard reed deze auto?

$6,9 +(298,5)/v = 14$ geeft $v ~~ 42$ km/h.

Iemand is geïnteresseerd in het verschil tussen de uitstoot bij een koude en bij een warme motor. Hij onderzoekt hoeveel procent de uitstoot bij een koude motor meer is dan bij een warme motor. Dat percentage hangt af van de snelheid. Hoe groot is dat percentage bij een snelheid van $30$ kilometer per uur?

Bij $v=30$ geldt voor de warme motor $u ~~ 10,93$ g/km en voor de koude motor $u ~~ 16,85$ g/km.

Het verschil is $(16,85 - 10,93)/(10,93) * 100 ~~ 54,2$ %.

Hoe kun je aan beide formules zien dat de koude motor altijd een hoger CO-emissie heeft dan de warme motor?

De koude motor begint met een hogere uitstoot en die wordt wel minder, maar blijft altijd boven de $6,9$ g/km (de asymptoot van de grafiek).

Er bestaan ook formules waarbij de CO-uitstoot gegeven wordt afhankelijk van de ritlengte en de rijtijd. Voor een warme benzinemotor geldt: $u_(text(tot))=4,4 L+0,054 T$ . Hierin is $u_(text(tot))$ de totale hoeveelheid CO in gram uitgestoten tijdens de rit, $L$ de ritlengte in kilometers en $T$ de rijtijd in seconden.

Laat zien hoe deze formule kan ontstaan uit de eerste formule voor de CO-uitstoot bij een warme motor.

Er geldt $v = 3600*L/T$ km/uur.

Vul dit in de formule $u=4,4 +(196,0)/v$ in: $u = 4,4 + (196,0)/((3600L)/T) ~~ 4,4 + (0,054T)/L$ .

$u_(text(tot)) = L * u = 4,4L + 0,054T$ .

Gegeven is de functie $y = 3sqrt(x) - 6$ .

Laat zien dat dit een getransformeerde machtsfunctie is.

$y = 3*(x)^(1/2) - 6$ .

Benoem de transformaties die nodig zijn om de grafiek van deze functie uit de bijbehorende standaardfunctie af te leiden.

Eerste vermenigvuldigen vermenigvuldigen met $3$ in de $y$ -richting en tenslotte $6$ omlaag verschuiven.

Bepaal de snijpunten van de grafiek van de gegeven functie met de beide assen.

Snijpunt met de $y$ -as: $(0, text(-)6)$ .

Snijpunt met de $x$ -as: $(4, 0)$ .

Snijpunt met de $y$ -as: $x=0$ geeft $y=text(-)6$ .
Het punt is $(0, text(-)6)$ .

Snijpunt met de $x$ -as: $y=0$ geeft $3sqrt(x) - 6 = 0$ .

Dit wordt $sqrt(x)=2$ en $2x=16$ , dus $x=4$ .
Het punt is $(4, 0)$ .

Los algebraïsch op: $3sqrt(x) - 6 le 9$ .

$0 le x le 24,5$ .

$3sqrt(x) - 6 = 9$ geeft $sqrt(x) = 5$ .

Kwadrateren geeft $x=25$ en dus $x = 25$ .

Grafiek: $0 le x le 25$ .

Gegeven de functie $y = (300-10x)/(2x)$ .

Laat zien dat dit een getransformeerde machtsfunctie is.

$y = 150*x^(text(-)1) - 5$

$y = (300-10x)/(2x) = 300/(2x) - (10x)/(2x) = 150/x - 5 = 150*x^(text(-)1) - 5$

Bepaal de asymptoten van de grafiek van de gegeven functie.

Verticale asymptoot $x = 0$ en horizontale $y=text(-)5$ .

De grafiek onstaat door die van $y = 1/x$ met $150$ in de $y$ -richting te vermenigvuldigen en tenslotte met $text(-)5$ in de $y$ -richting te verschuiven. De asymptoten verschuiven mee.

Verticale asymptoot $x = 0$ en horizontale $y=text(-)5$ .

Bereken het nulpunt van de grafiek van de gegeven functie.

$(30, 0)$

$150/x - 5=0$ geeft $150/x=5$ en dus $x=150/5 = 30$ .
Het nulpunt is $(30, 0)$ .

Los op in twee decimalen nauwkeurig: $(300-10x)/(2x) ≥ 40$ .

$0 lt x le 3,33$

$150/x - 5 = 40$ geeft $150/x=45$ en dus $x=150/45 ~~ 3,33$ .

Grafiek: $0 lt x le 3,33$ .