In dit onderwerp heb je gewerkt met machten en heb je ontdekt dat veel functies met wortels en/of breukvormen als machtsfunctie met gebroken en/of negatieve exponenten zijn te schrijven. Verder heb je kennis gemaakt met verschuivingen en vermenigvuldigingen van grafieken. Veel functies kunnen daarmee ontstaan uit een standaardfunctie waarvan de eigenschappen bekend zijn.
Je hebt nu alle theorie van
Geef van de volgende functies aan of recht evenredig is met een macht van of juist omgekeerd evenredig met een macht van of geen van beide. Laat zien hoe de functie als machtsfunctie kan worden geschreven.
Recht evenredig met .
Is al een machtsfunctie.
.
Recht evenredig met .
.
is omgekeerd evenredig met en recht evenredig met .
.
Er is nu geen sprake van een recht evenredig of een omgekeerd evenredig verband. Deze functie is ook geen machtsfunctie.
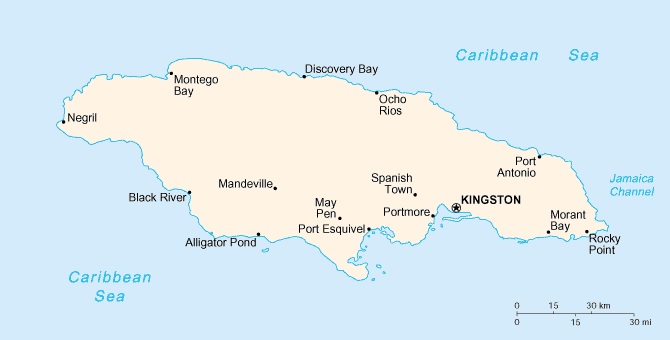
Het lijkt aannemelijk dat er een verband bestaat tussen de oppervlakte van een gebied en het aantal verschillende diersoorten dat in dat gebied voorkomt. Een theorie hierover stelt dat het aantal verschillende diersoorten op een eiland in een bepaalde klimaatzone alleen afhankelijk is van de oppervlakte van het eiland. In deze opgave kijken we naar de verschillende soorten reptielen op eilanden in het Caraïbisch gebied. Onderzoekers telden op vele eilanden het aantal verschillende soorten reptielen.
Ze ontdekten een verband tussen de oppervlakte van een eiland (in vierkante mijlen) en het aantal soorten reptielen () op dat eiland: .
Het eiland Jamaica is ongeveer vierkante mijlen groot. Er zijn meer soorten reptielen aangetroffen dan op grond van deze formule verwacht mag worden.
Hoeveel soorten reptielen zou een even groot eiland volgens de theorie hebben? Licht je antwoord toe.
Volgens de theorie dus .
Binnen de theorie geldt als ruwe regel:
Op een groot eiland worden veel verschillende soorten reptielen met uitsterven bedreigd. Men wil maatregelen nemen om de natuur te beschermen. Daarbij moet er een keuze worden gemaakt uit twee mogelijkheden:
Oprichting van één groot natuurreservaat met een oppervlakte van vierkante mijlen.
Oprichting van twee kleinere reservaten, elk met een oppervlakte van vierkante mijlen. Dergelijke natuurreservaten liggen geïsoleerd in de bewoonde wereld en kunnen als 'eilanden' beschouwd worden.
Voor het schatten van het aantal soorten reptielen dat in zo’n reservaat zal voorkomen kan de formule gebruikt worden. Welke mogelijkheid gekozen wordt, is mede afhankelijk van het aantal soorten dat de twee kleinere reservaten gemeen zullen hebben. Men neemt aan dat er soorten reptielen zijn die zowel in het éne als het andere kleine reservaat zullen voorkomen. Men wil de mogelijkheid kiezen waarbij in totaal zoveel mogelijk verschillende soorten reptielen zullen voorkomen.
Welke van de twee mogelijkheden zal men kiezen? Licht je antwoord toe.
Grote reservaat zal ongeveer soorten tellen. Elk van de kleine reservaten zal ongeveer soorten tellen, samen soorten. Men kiest de tweede oplossing.
Gegeven is de functie .
Laat zien door welke transformaties de grafiek van kan ontstaan uit die van .
naar rechts schuiven, dan met vermenigvuldigen in de -richting en tenslotte omhoog schuiven.
Bereken algebraïsch de snijpunten van de grafiek van de gegeven functie met de beide coördinaatassen.
Het snijpunt met de -as is .
Het snijpunt met de -as is .
Snijpunt met de -as: geeft , dus snijpunt -as is .
Snijpunt met de -as: geeft en dus , dus het snijpunt met de -as is .
Los algebraïsch op: .
.
geeft en dus .
Los algebraïsch op: .
De oplossing van de ongelijkheid is .
geeft en dus .
Grafiek: .
Herleid de volgende functies naar de vorm .
Herleid de volgende functies naar wortelfuncties en/of gebroken functies.
of .
.
of:
.
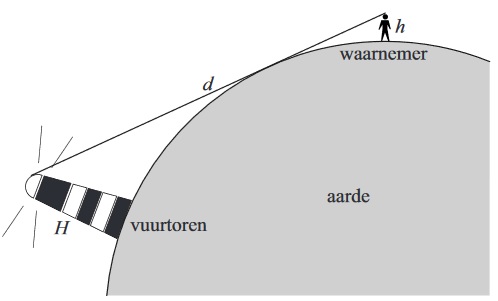
Het licht van de Lange Jaap, een vuurtoren bij Den Helder, reikt zeemijl ver. Een zeemijl is m.
De lamp van de Lange Jaap bevindt zich op een hoogte van m. Vanaf een kijkhoogte van m is het licht van de Lange Jaap op een afstand van zeemijl niet (rechtstreeks) te zien, omdat de vuurtoren zich dan achter de horizon bevindt.
De maximale afstand waarop het licht van een vuurtoren een waarnemer (rechtstreeks) kan bereiken is afhankelijk van de hoogte waarop de lamp van een vuurtoren zich bevindt en van de kijkhoogte van de waarnemer.
Bij benadering geldt:
Hierin is:
de maximale afstand in km waarop het licht van een vuurtoren een waarnemer (rechtstreeks) kan bereiken
de hoogte van het licht van de vuurtoren in m
de kijkhoogte in m
Laat zien dat voor de Lange Jaap geldt m.
Vul in en je vindt .
Dit levert de gewenste formule op.
De formule voor de kijkafstand van de Lange Jaap (zie a) is een getransformeerde machtsfunctie.
Leg uit welke machtsfunctie dat is en om welke transformaties het gaat.
De machtsfunctie is .
De transformaties zijn:
vermenigvuldiging met in de verticale richting en
verschuiving van in de verticale richting.
Op welke kijkhoogte is de lamp van de Lange Jaap op een afstand van zeemijl nog zichtbaar?
De afstand is m.
Los op .
Je vindt: en zodat m.
De formule voor de kijkafstand uit het begin van het onderwerp
Neem eens aan dat de aarde een zuivere bol is met een omtrek van km. De hoogte (in m) is de afstand van je ogen tot het aardoppervlak. In de tekening zie je hoe dat er dan in doorsnede uit ziet. De kijkafstand (in m) is dan de lengte van (eigenlijk van de boog maar dat verschilt niet veel van elkaar).
Hoe kun je nu berekenen? Maak zo een formule voor afhankelijk van .
kun je berekenen met de stelling van Pythagoras in . (Beredeneer eerst dat rechthoekig is!) Daarin is gelijk aan de straal van de aarde, dus m. En dus is: . En dus is .
Hieruit volgt: .
Omdat heel veel kleiner is dan kun je verwaarlozen.
Laat zien dat ongeveer geldt .
Dan is .
De gevonden formule is iets anders dan die aan het begin van het onderwerp
Dat heeft te maken met de afrondingen bij het berekenen van de straal van de Aarde.
Je kunt zo ook een formule afleiden voor de kijkafstand op de maan. Zoek de daarvoor benodigde gegevens op en leidt die formule af.
Eigen antwoord.
Kun je op de maan verder of minder ver kijken dan op Aarde?
En?
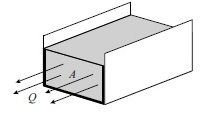
Via een rechthoekige goot loost een fabriek koelwater op een rivier. De hoeveelheid koelwater die per seconde een dwarsdoorsnede van een goot passeert, wordt het debiet van de goot genoemd.
Het debiet van de goot van de fabriek is te berekenen met de formule:
Hierin is:
is het debiet in m
is de oppervlakte van de rechthoekige dwarsdoorsnede van het water in m
is de totale lengte van de randen van de dwarsdoorsnede die onder water liggen in m. In de bovenste figuur zijn die randen dikgedrukt.

De rechthoekige goot waarmee de fabriek het koelwater loost, is meter breed en meter hoog. Hiernaast is de dwarsdoorsnede van deze goot getekend bij een maximaal debiet.
De fabriek loost m
Bereken het maximale debiet en leid daaruit af of de goot tijdens deze lozing zal overstromen.
Het maximale debiet is ongeveer m
en invullen in de formule geeft dus het maximale debiet is ongeveer m
m
Conclusie: de goot zal niet overstromen.
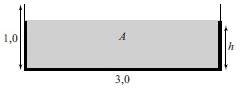
De waterhoogte in de goot noemen we , met in m.
Bij normale lozing stroomt er continu m
Bereken in dit geval de waterhoogte in de goot. Geef je antwoord in centimeter nauwkeurig.
De gevraagde hoogte is meter.
De vergelijking moet opgelost worden.
Invoeren in de GR: en . Het snijpunt bepalen geeft .
De gevraagde hoogte is meter.