het begrip logaritme en enkele eigenschappen ervan kennen;

logaritmen berekenen;

exponentiële vergelijkingen oplossen met behulp van logaritmen.

werken met exponentiële functies, ook met GeoGebra of een grafische rekenmachine;

werken met de begrippen macht, grondtal en exponent.

Inwoners V.S.

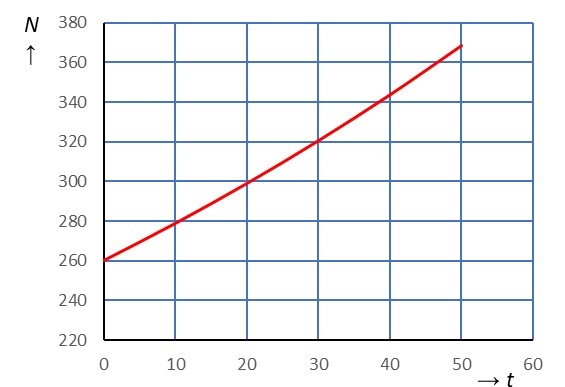
In $1995$ had de V.S. $260$ miljoen inwoners. Elk jaar neemt dit aantal toe met $0,7$ %.

Welk getal is de groeifactor per jaar?

$1,007$ .

Er geldt: $N(t)=260*(1,007)^t$
met $N$ het aantal inwoners in miljoenen en $t$ in jaren ( $t=0$ in $1995$ ).

Bereken het aantal inwoners in $2015$ . Klopt dat met de grafiek?

$~~299$ miljoen.

$2015-1995=20$ jaar, $N(20)=260*(1,007)^20~~299$ miljoen.

Schat in welk jaar het aantal inwoners in de V.S. $340$ miljoen bedraagt.

Na $38$ jaar (aflezen).

Een hoeveelheid bacteriën groeit exponentieel. Voor de hoeveelheid bacteriën $B$ in een petrischaaltje geldt $B = 2 * 10^t$ met $t$ in uur. Na hoeveel uur (in minuten nauwkeurig) zijn er $1200$ bacteriën?
$2 *10^t=1200$ geeft: $10^t=600$
Met een grafiek vind je de oplossing $t~~2,78$ .
Dit antwoord is afgerond.
De exacte oplossing schrijf je als: $t= log(600)$ .
Dit is de logaritme van $600$ met grondtal $10$ .
Het grondtal $10$ schrijf je niet op, ook op een rekenmachine zie je dit grondtal niet.

Bekijk de bacteriegroei in Uitleg.

Je wilt weten na hoeveel tijd de hoeveelheid bacteriën $5000$ is.
Schrijf het antwoord als logaritme en bepaal het in twee decimalen nauwkeurig.

$2 * 10^t = 5000$ geeft $10^t = 2500$ en dus $t = log(2500)$ .
Met de grafiek van $y = 10^t$ (zie de applet) vind je $t = log(2500) ~~ 3,40$ .

Los nu met behulp van een logaritme op: $10^t = 1000$ .
Waarom komt de waarde van $t$ op een geheel getal uit?

Je vindt $t = log(1000) = 3$ .
En dat is nogal logisch, want $10^3 = 10*10*10 = 1000$ .

Controleer dat ook met de applet deze waarde voor $t$ wordt gevonden.

Stel de schuifknop in op $1000$ .

Je hebt gezien hoe je een vergelijking zoals $10^t = c$ kunt oplossen met behulp van een logaritme met grondtal $10$ .

In welke gevallen wordt de oplossing een geheel getal?

Als in $10^t = c$ de $c$ een macht van $10$ is.

Laat door berekening zien, dat $log(10^3) = 3*log(10)$ .

$log(10^3) = 3$ en $3*log(10) = 3*1 = 3$ .

Waarom geldt in het algemeen $log(10^t) = t*log(10)$ ?

$log(10^t) = t$ en $t*log(10) = t*1 = t$ .

Ga met je rekenmachine na, dat ook $log(2^3) = 3*log(2)$ .
Controleer dit ook voor andere getallen.

Beide komen uit op $0,093...$ .
Welke getallen je ook kiest, altijd is $log(g^t) = t*log(g)$ .

Welke eigenschap van logaritmen geldt dus?

$log(g^t) = t*log(g)$

Voor een andere bacteriekolonie geldt: $B = 4 * 1,5^t$ .
Hierin is $B$ het aantal bacteriën en $t$ de tijd in uren.

Als je nu wilt weten na hoeveel tijd je $1000$ bacterieën hebt, dan moet je oplossen:

$4*1,5^t=1000$

Eerst beide zijden delen door $4$ geeft:

$1,5^t=250$

Ook een dergelijke vergelijking kun je met behulp van logaritmen oplossen.
Je gebruikt dan de eigenschap $log(g^t) = t*log(g)$ .

$1,5^t=250$ los je op door aan beide zijden de logaritme te nemen: $log(1,5^t)=log(250)$ .
De eerder genoemde eigenschap geeft dan $t * log(1,5) = log(250)$ .
En dus is $t = (log(250))/(log(1,5))$ .
En dit kun je gewoon met je rekenmachine berekenen: $t = (log(250))/(log(1,5)) ~~ 13,62$ .

De oplossing van $1,5^t=250$ wordt wel kortweg genoteerd als $t = \ ^(1,5)log(250)$ .
Dit is een logaritme met grondtal $1,5$ .
Met de oplossing die je eerder zag betekent dit $\ ^(1,5)log(250) = (log(250))/(log(1,5))$ .

Bekijk Uitleg.

Los zelf de vergelijking $4*1,5^t=2000$ op met behulp van de 10-logaritme.

$4*1,5^t=1000$ geeft eerst $1,5^t = 500$ .
Beide zijden 10-logaritme nemen: $log(1,5^t) = log(500)$ .
Eigenschap gebruiken: $t*log(1,5) = log(500)$ en dus is $t = (log(500))/(log(1,5)) ~~ 15,33$ .

Schrijf de oplossing van de vergelijking $1,5^t=500$ op als één logaritme.

$t = \ ^(1,5)log(500)$

Hoe bereken je $\ ^(1,5)log(500)$ op je rekenmachine?

$t = \ ^(1,5)log(500) = (log(500))/(log(1,5)) ~~ 15,33$

Een bacteriekolonie groeit volgens de formule $B = 6*5^t$ met $t$ de tijd in uren en $B$ het aantal bacteriën.

Bereken met behulp van logaritmen na hoeveel tijd er $6000$ bacteriën zijn.
Geef je antwoord in twee decimalen nauwkeurig.

$B = 6*5^t = 6000$ geeft $5^t = 1000$ en dus $t = \ ^5log(1000) = (log(1000))/(log(5)) ~~ 4,29$ uur.

Bereken met behulp van logaritmen de verdubbelingstijd in twee decimalen nauwkeurig.

$6*5^t = 12$ geeft $5^t = 2$ en dus $t = \ ^5log(2) = (log(2))/(log(5)) ~~ 0,43$ uur.

De 10-logaritme $x= log(c)$ is de oplossing van $10^x=c$ .

Dus geldt dan ook:

$log(10^c)=c$ en $10^(log(c)) =c$

De 10-logaritme is de terugrekenbewerking van de exponentiële functie met grondtal $10$ en omgekeerd.

De $g$ -logaritme $x=\ ^(g)log(c)$ is de oplossing van $g^x=c$ .

Ook hier geldt:

$\ ^(g)log(g^c)=c$ en $g^ (\ ^(g)log(c)) = c$

De logaritme $\ ^(g)log(c)$ heeft alleen betekenis als $0 lt g lt 1$ of $g gt 1$ en $c gt 0$ .

Het verband tussen $\ ^(g)log(c)$ en $log(c)$ is:

$\ ^(g)log(c) = (log(c))/(log(g))$ .

Hiermee kun je logaritmen met een willekeurig grondtal op een rekenmachine berekenen.
Soms gaat dit ook rechtstreeks, het grondtal staat dan rechts onder de log: $log_(g) (c)$ .

Luchtschepen zijn gevuld met gas met een lage soortelijke massa. Dat gas staat onder druk en er lekt een klein deel van weg.
Een luchtschip met een inhoud van $3000$ m3 verliest elke tien dagen ongeveer $2$ % van het gas. Als er minder dan $2400$ m3 over is, kan het luchtschip niet meer vliegen. Hoeveel dagen kan het luchtschip vliegen als het geheel is gevuld met gas? Geef je antwoord met een logaritme, en als een benadering afgerond op twee decimalen.

De hoeveelheid gas in het luchtschip is $G = 3000 *0,98^t$ met $G$ in m3 en $t$ in eenheden van tien dagen.

Los op: $3000 *0,98^t = 2400$ .

$3000 *0,98^t$

$=$

$2400$

$0,98^t$

$=$

$0,8$

$t$

$=$

$\ ^(0,98)log(0,8 ) = (log(0,8))/(log(0,98))≈11,05$

Gebruik hierbij de log-knop van je rekenmachine.

Het luchtschip kan $110$ dagen vliegen zonder bijvullen. Op dag $111$ kan het luchtschip niet meer vliegen.

Uit een luchtschip met een inhoud van $3000$ m3 vervliegt per tien dagen $4$ % van het gas.
Na hoeveel dagen is de inhoud van het luchtschip verminderd tot $2800$ m3?

Stel de vergelijking voor dit probleem op en vereenvoudig deze zo ver mogelijk.

Let er op dat de variabele $t$ in eenheden van tien dagen is.
De groeifactor is dan per $10$ dagen gelijk aan $0,96$ en de beginhoeveelheid is $3000$ .

De bijbehorende vergelijking wordt $3000 *0,96^t = 2800$ .
Dit vereenvoudig je tot $0,96^t=14/15$ .

Geef de oplossing van de vergelijking als logaritme. Geef ook een benadering afgerond op twee decimalen.

$t=\^(0,96)log(14/15) = (log(14/15))/(log(0,96)) ≈ 1,69$

Een hoeveelheid bacteriën neemt per dag met $20$ % toe.

Bepaal de bijbehorende groeifactor.

De groeifactor is $1,2$ .

Een bioloog wil weten na hoeveel dagen het aantal bacteriën is verdubbeld. Stel de vergelijking voor dit probleem op en vereenvoudig deze vergelijking zo ver mogelijk.

Je moet het aantal $2$ keer zo groot maken en je vermenigvuldigt elke tijdseenheid met $1,2$ , dus moet $1,2^t = 2$ .

Schrijf de oplossing van de vergelijking als een logaritme en beantwoord daarmee de vraag.

$t=\ ^(1,2)log(2) = (log(2))/(log(1,2)) = 3,80178...$

Na $3,8$ dagen is de hoeveelheid bacteriën nog nét niet verdubbeld.
Na vier dagen is de hoeveelheid verdubbeld.

De luchtdruk varieert met de hoogte boven het zeeniveau. Er geldt:

$p = 1013 * 10^(text(-)0,065h)$

Hierin is:

$p$ de druk in hectopascal

$h$ de hoogte in km boven zeeniveau

In deze formule wordt het standaard grondtal $10$ gebruikt, de groeifactor is niet onmiddellijk zichtbaar. Hoe kun je aan deze formule zien dat er van exponentiële afname sprake is? Bereken de bijbehorende halveringshoogte, de hoogte waarin de luchtdruk wordt gehalveerd.

Je kunt de formule schrijven als $p = 1013 * (10^(text(-)0,065))^h$ .
De groeifactor is dus $10^(text(-)0,065) ~~ 0,86$ .
Deze groeifactor is kleiner dan $1$ en dus is er van exponentiële afname sprake.

De halveringshoogte vind je uit $10^(text(-)0,065h) = 0,5$ .
Dit betekent: $text(-)0,065h = log(0,5) ~~ text(-)0,301$ (standaard grondtal $10$ ).
En dus wordt de halveringshoogte: $h ~~ (text(-)0,301)/(text(-)0,065) ~~ 4,63$ km.

Bekijk de formule voor de luchtdruk $p$ (in hectopascal) als functie van het hoogte $h$ (in km) in Voorbeeld.

De groeifactor is $10^(text(-)0,065)$ . Waarom kun je al meteen aan het negatiefteken zien dat er sprake is van exponentiële afname?

$10^0 = 1$ , met zo'n groeifactor is er geen groei of afname.
Als in $10^a$ de $a$ negatief is, is $10^a lt 10^0 lt 1$ en heb je met exponentiële afname te maken.

Waarom is het gebruik van het standaardgrondtal $10$ handig?

Omdat je dan bij het oplossen van vergelijkingen meteen de log-knop kunt gebruiken zonder delingen te maken.

Op welke hoogte is nog maar een kwart van de luchtdruk op zeeniveau over?

Dat is twee keer de halveringshoogte: $h ~~ 2 * 4,63 ~~ 9,26$ km.

Op welke hoogte is nog maar éénvijfde van de luchtdruk op zeeniveau over?

Je moet nu oplossen: $10^(text(-)0,065h) = 0,2$ .
Dit betekent: $text(-)0,065h = log(0,2) ~~ text(-)0,699$ .
En dus: $h ~~ (text(-)0,699)/(text(-)0,065) ~~ 10,75$ km.

Voor een bacteriekolonie geldt: $B = 4 * 1,5^t$ .
Hierin is $B$ het aantal bacteriën en $t$ de tijd in uren.

Laat met je rekenmachine zien, dat $1,5 = 10^(log(1,5)) ~~ 10^(0,176)$ .

Type $10^(log(1,5))$ in en je vindt als antwoord $1,5$ .
Verder is $log(1,5)~~0,176$ .

Laat hiermee zien dat de formule voor de bacteriegroei kan worden geschreven als $B = 4*10^(0,176t)$ .

$B = 4*1,5^t = 4*(10^(log(1,5)))^t ~~ 4 * (10^(0,176))^t = 4*10^(0,176t)$

Vanaf welk tijdstip zijn er meer dan $150$ bacteriën?
Gebruik de formule bij b.

Los op: $4*10^(0,176t) = 150$ .
Je vindt $10^(0,176t) = 15$ en dus $0,176t = log(15) ~~ 1,176$ .
Dus: $t ~~ (1,176)/(0,176) ~~ 6,68$ uur.
Er is meer dan $150$ mg bacteriën als $t le 6,68$ uur.

Een hoeveelheid bacteriën groeit volgens de formule $B = 3*7^t$ waarin $t$ de tijd in uren is en $B$ de hoeveelheid bacteriën.

Bereken in twee decimalen nauwkeurig met behulp van logaritmen na hoeveel uur er $6000$ bacteriën zijn.

$3*7^t = 6000$ geeft $7^t = 2000$ en dus $t = \ ^7log(2000) = (log(2000))/(log(7)) ~~ 3,91$ uur.

Bereken in twee decimalen nauwkeurig de verdubbelingstijd van de bacteriegroei.

$3*7^t = 6$ geeft $7^t = 2$ en dus $t = \ ^7log(2) = (log(2))/(log(7)) ~~ 0,36$ uur.

Schrijf de oplossing van de vergelijkingen als logaritme. Geef daarna indien nodig een benadering in één decimaal.

$10 *10^x=0,1$

$10^x=0,01$ . En dus: $x=log(0,01 )= text(-)2$ .

$0 ,5 *2^x=30$

$2^x=60$ . Hieruit volgt: $x=\ ^2log(60) = (log(60))/(log(2)) ≈5,9$

$54 *0,8^t=27$

$0,8^t=0,5$ . Hieruit volgt: $t=\ ^(0,8)log(0,5 ) = (log(0,5))/(log(0,8)) ≈3,1$

Een kolonie bacteriën groeit exponentieel met groeifactor $2$ per uur.

Bereken in minuten nauwkeurig hoelang het duurt voordat de kolonie zich heeft verdrievoudigd. Maak bij de berekening gebruik van een logaritme.

$t=\ ^2log(3) = (log(3))/(log(2)) ≈1,58$ uur.
Na ongeveer $1$ uur en $35$ minuten heeft de kolonie zich verdrievoudigd.

Omstreeks 1650 groeide de wereldbevolking met een percentage van $0,3$ % per jaar.
Geef de verdubbelingstijd als logaritme en geef een benadering in gehele jaren.

De verdubbelingstijd is $\ ^(1,003)log(2)=(log(2 )) / (log(1,003 )) ≈231$ jaar.

Een radioactieve stof vervalt volgens deze formule: $N = N_0 *0,93^t$
$N$ is de hoeveelheid in milligram en $t$ de tijd in jaar.
$N_0$ is de hoeveelheid op $t=0$ .

Bereken de halveringstijd. Rond af op twee decimalen.

$t=\ ^(0,93)log(0,5 )≈9,55$ jaar

Een laboratorium heeft $400$ gram van deze stof. Bereken met behulp van de halveringstijd hoelang het duurt voordat deze hoeveelheid minder is geworden dan $50$ gram. Rond af op één decimaal.

$400 →200 →100 →50$
Hieruit volgt dat er drie halveringstijden zijn en dat geeft $3 *9,55 ~~28,7$ jaar.

Bereken tot op een maand nauwkeurig hoelang het duurt voordat $50$ gram van deze stof minder is geworden dan $10$ gram.

$50 *0,93^t$

$=$

$10$

$0,93^t$

$=$

$0,2$

$t$

$=$

$\ ^(0,93)log(0,2 )≈22,18$

Dit is ongeveer $22$ jaar en $2$ maanden.

Olievervuiling

Ramp! Olietanker verliest totale lading olie op $15$ km uit de kust.
De ramp speelde zich af om $5$ uur in de ochtend. De olievlek had toen een grootte van $0,16$ km2. De olie verspreidt zich zo, dat deskundigen beweren dat de oppervlakte ( $A$ ) van de vlek iedere dag $10$ keer zo groot wordt.

Bereken de grootte van de olievlek op woensdagochtend om $5$ uur.

$0,16*10^2=16$ km2.

Er geldt: $A=0,16*10^t$
met $A$ het vervuild oppervlak in km2 en $t$ in dagen.

Controleer jouw berekening bij a met deze formule.

Zie a.

We nemen aan dat de olievlek de vorm van een cirkel heeft.

Bereikt de olievlek de kust op woensdagochtend?

De vlek bereikt de kust niet.

$pi r^2=16 rarr r^2=5,1 rarr r~~2,3$ km.

Op welke dag is de grootte van de olievlek $500$ km2? Wordt de kust dan bereikt?

Donderdag om $17.00$ uur.

$0,16*10^t$

$=$

$500$

$10^t$

$=$

$500/(0,16)$

$10^t$

$=$

$3125$

$t$

$=$

$3,5$ (10 $log3125$ )

$pi r^2=500 rarr r^2=159 rarr r~~136$ km.

Bereken dag en tijdstip waarop de olie de kust bereikt.

Donderdag om $20.36$ uur.

$r=15 rarr A=pi r^2=pi*225=706,86$ km2.

$0,16*10^t$

$=$

$706,86$

$10^t$

$=$

$706,86/(0,16)$

$10^t$

$=$

$4417,9$

$t$

$=$

$log(4417,9)~~3,65$ dus $3$ dagen en $15,6$ uur.

Vermogensversterking

Signalen die onze huizen binnenkomen (radio/tv) hebben een lage sterkte. Om ze hoorbaar/zichtbaar te maken, worden ze versterkt met behulp van een versterker. In de elektrotechniek spreekt men over vermogens ( $P$ ) versterking en/of spanningsversterking. Voor spanning wordt het symbool $U$ (in volt) gebruikt.
Een vermogensversterking $X$ wordt uitgedrukt in dB (decibel) volgens:
$X=10*log((P_u)/(P_i))$

Hierin is:

$P_u$ het vermogen aan de uitgang (dat vrijkomt) in Watt

$P_i$ het vermogen aan de ingang (dat versterkt moet worden) in Watt

Laat zien dat bij $P_i=10^(text(-)3)$ Watt en $P_u=20$ Watt er een vermogensversterking is van $43$ dB.

$X=10*log((P_u)/(P_i))=10*log(20/10^(text(-)3))=43$ dB.

Bereken $P_u$ bij een versterking van $46$ dB en $P_i=10^(text(-)3)$ Watt.

$46$

$=$

$10*log((P_u)/(10^(text(-)3)))$

$4,6$

$=$

$log((P_u)/(10^(text(-)3)))$

$(P_u)/(10^(text(-)3))$

$=$

$10^(4,6)$

$P_u$

$=$

$10^(1,6)=39,8$ Watt.

Ook de spanningsversterking bij een versterker wordt uitgedrukt in dB. Er geldt dat $P_u$ evenredig is met $U_u^2$ en $P_i$ met $U_i^2$ .

Leidt uit $X=10*log((P_u)/(P_i))$ de formule $X=20*log((U_u)/(U_i))$ af.

$X$

$=$

$10*log((P_u)/(P_i))$

$=$

$10*log((U_u^2)/(U_i^2))$

$=$

$10*log((U_u)/(U_i))^2$

$=$

$20*log((U_u)/(U_i))$ .

Gegeven is $U_i=1$ Volt en een spanningsversterking van $X=text(-)20$ dB.
Bereken $U_u$ . Wat is de betekenis van een negatieve spanningsversterking?

$text(-)20$

$=$

$20*log((U_u)/1)$

$log(U_u)$

$=$

$text(-)1$

$U_u$

$=$

$10^(text(-)1)$

$=$

$0,1$ Volt.

Een negatieve spanningsversterking betekent dat je te maken hebt met een verzwakker.

Los de volgende vergelijkingen op. Schrijf de oplossing als logaritme en geef daarna een benadering in twee decimalen nauwkeurig.

$6 *4^x=35$

$x=\ ^4 log(35/6)≈1,27$

$4^x=35/6$ , dus $x=\ ^4log(35/6)=(log(35/6))/(log(4))≈1,27$ .

$1050 *1,08^t=1800$

$t=\ ^(1,08) log(12/7)≈7,00$

$1,08^t=12/7$ , dus $t=\^(1,08)log(12/7)=(log(12/7))/(log(1,08))≈7,00$ .

In een tank zit $150$ liter verontreinigde vloeistof. Deze vloeistof wordt verwijderd door spoelen met water. Hierdoor verdwijnt elke minuut $15$ % van de vloeistof. Men wil stoppen met spoelen als er minder dan $10$ liter verontreinigde vloeistof over is.

Bereken hoe lang men moet spoelen. Schrijf het antwoord als logaritme en geef een benadering van deze logaritme.

$t=\ ^(0,85) log(1/15)≈16,7$ . Dus na $17$ keer spoelen.

$150 *0,85^t=10$ , geeft $0,85^t=1/15$ en dus $t=\ ^(0,85)log(1/15)≈16,7$ .
Dus na $17$ keer spoelen.