werken met logaritmische functies;
vergelijkingen met logaritmen oplossen met behulp van exponenten.
werken met exponentiële functies, ook met GeoGebra of een grafische rekenmachine;
werken met logaritmen en enkele eigenschappen ervan;
exponentiële vergelijkingen oplossen met behulp van logaritmen.
Een logaritmische functie heeft een formule zoals .
Het grondtal van deze logaritme is , dus je kunt deze grafiek vergelijken met die van .
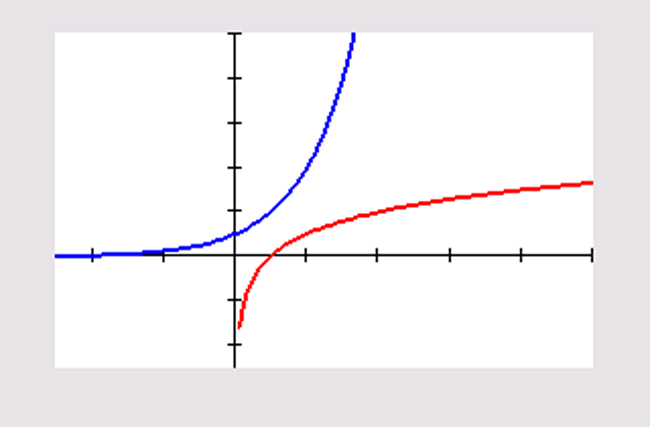
Maak de grafiek van deze functies in één figuur.
Zie de figuur.
Je ziet dat beide grafieken erg op elkaar lijken, ze zijn elkaars spiegelbeeld.
In welke lijn moet je dan spiegelen?
De lijn .
Welke asymptoten hebben de beide grafieken?
De grafiek van heeft de -as als asymptoot.
De grafiek van heeft de -as als asymptoot.
Laat met een paar getallenvoorbeelden zien, dat en dat .
Neem b.v. : en .
Je ziet hier de grafieken van en .
Ze zijn elkaars spiegelbeeld in de lijn .
is een logaritmische functie met:
nulpunt bij ;
een stijgende grafiek;
verticale asymptoot .
Je kunt er alleen positieve -waarden invullen.
Je ziet dat de eigenschappen het spiegelbeeld zijn van die van .
Ze zijn elkaars terugrekenfunctie: en .
Voor logaritmische functies met andere grondtallen geldt .
Ze hebben daarom dezelfde eigenschappen als .
Bekijk de grafieken van en .
Het punt ligt op de grafiek van . Welk punt op de grafiek van is het spiegelbeeld van dit punt bij spiegeling in de lijn ?
Noem nog twee punten op de grafiek van en geef voor beide punten het bijbehorende spiegelbeeld op de grafiek van .
Bijvoorbeeld: en of en
Laat met een voorbeeld zien dat en elkaars terugrekenfunctie zijn.
Voor bijvoorbeeld in in en je krijgt .
Voer deze in in en je krijgt .
Los op .
Houd rekening met de -waarden die je in een logaritme mag invullen.
Als je in beide zijden een exponentiële functie met grondtal toepast, krijg je omdat deze functie aan de linkerkant de logaritme wegwerkt. Dus de oplossing van is .
In de grafiek zie je nu dat als oplossing heeft .
Bekijk de grafieken van en .
Maak beide grafieken.
Voer in een grafische rekenmachine in: en of .
Voer in GeoGebra in: en .
Venster bijvoorbeeld: en .
Het punt ligt op de grafiek van . Welk punt op de grafiek van is het spiegelbeeld van dit punt bij spiegeling in de lijn ?
Noem nog twee punten op de grafiek van en geef voor beide punten het bijbehorende spiegelbeeld op de grafiek van .
Bijvoorbeeld: en of en
Los op .
geeft .
Grafiek: .
Laat zien, dat .
.
Plot de grafieken van en .
De eigenschappen van kun je afleiden uit die van .
Welke asymptoot heeft de grafiek van ?
De verticale asymptoot is .
Voor welke waarde van is ?
Dus voor .
Los op .
geeft .
Grafiek: .
Laat zien, dat .
.
Een functie van de vorm heet een
is het grondtal. Er moet gelden: en
De grafieken van de functies en zijn elkaars
De karakteristieken van zijn af te leiden uit die van :
alleen -waarden boven zijn toegestaan;
als is de grafiek stijgend, als dalend
de -as is de verticale asymptoot van de grafiek
Alle functies die door transformatie uit kunnen ontstaan, heten logaritmische functies.
Gegeven is de logaritmische functie .
Maak de grafiek van deze functie en los op .
De grafiek zie je hier.
los je zo op:
beide zijden
beide zijden delen door
beide zijden exponentiële functie met grondtal
In de grafiek zie je dat de oplossing van de ongelijkheid is .
Bekijk in
Welke asymptoot heeft deze functie?
Welke waarden van mag je er invullen?
Verticale asymptoot .
Je mag alleen -waarden invullen met .
Voor welke waarden van is ?
los je zo op:
beide zijden
beide zijden delen door
beide zijden exponentiële functie met grondtal
In de grafiek zie je dat de oplossing van de ongelijkheid is .
Gegeven is de functie .
Laat zien dat deze functie te schrijven is als .
.
Los op: . Geef een benadering in twee decimalen.
geeft en dus .
Grafiek: .
In een luchtballon kun je de hoogte bepalen door de luchtdruk te meten met een barometer. In het gebied waar de ballon vliegt geldt bij een gegeven temperatuur op de grond:
Hierin is:
de luchtdruk in hectopascal
de hoogte in km boven zeeniveau
Er wordt een luchtdruk van ongeveer hPa gemeten.
Op welke hoogte zit de ballon dan?
Hoe groot is de luchtdruk als je hoger dan km zit?
invullen geeft km.
Als je hoger dan km zit, geldt: .
De bijbehorende vergelijking kun je oplossen: .
Dus de luchtdruk is dan lager dan hPa.
Bekijk de logaritmische functie in
Laat zien hoe je oplost.
Bijvoorbeeld zo:
Hoeveel bedroeg de luchtdruk op de begane grond?
betekent .
Dit los je net zo op als bij a:
geeft en dus hPa.
Een andere formule voor het berekenen van de hoogte in km afhankelijk van de luchtdruk in hPa is:
Laat zien dat je dit kunt schrijven als .
.
Hoeveel bedraagt de luchtdruk op de begane grond?
geeft en dus .
Hieruit volgt hPa.
Op welke hoogte wordt de luchtdruk in dit gebied lager dan hPa?
km.
Een logaritmische functie is gegeven door .
Maak de grafiek van deze functie.
Gebruik GeoGebra, Desmos of een grafische rekenmachine.
Welke verticale asymptoot heeft de grafiek?
De -as.
Los op: .
geeft , dus .
Grafiek: .
Gegeven is de formule .
Herleid deze formule tot een formule met een logaritme met het standaardgrondtal .
.
Lichtgevoeligheid van fotografisch opnamemateriaal wordt uitgedrukt in een gevoeligheidsgetal. Het meest gebruikte systeem hiervoor is het ISO/ASA-systeem. Vroeger werd vaak een ander gevoeligheidsgetal gebruikt, de DIN-waarde. Het verband tussen ISO en DIN wordt gegeven door de formule:
Hierin geeft de lichtgevoeligheid in ISO aan en de lichtgevoeligheid in DIN. Een film van ISO heeft een DIN-waarde van .
Bereken .
Maak de bijbehorende grafiek. Laat lopen tot .
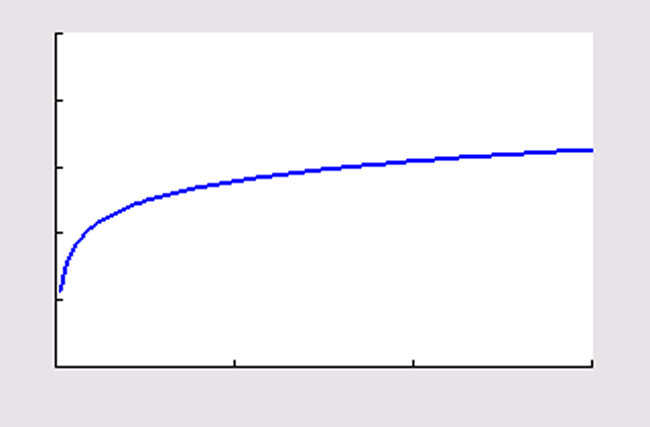
Voer in .
Venster bijvoorbeeld en .
Welke ISO-waarde heeft een film met een gevoeligheid van DIN?
De ISO-waarde is .
Vliegtuigen veroorzaken in de buurt van vliegvelden veel geluidsoverlast. In milieuwetten is vastgelegd welke geluidsbelasting (hoeveel geluid) nog toegestaan is. Door deze wetten worden de groeimogelijkheden van het vliegverkeer beperkt.
In deze opgave nemen we aan dat alle vliegtuigen hetzelfde geluidsniveau hebben. Dit geluidsniveau geven we aan met . De waarde van bepaalt hoeveel vliegtuigen jaarlijks maximaal mogen passeren. Dit maximale aantal noemen we . Voor een gebied in de buurt van vliegveld Zuidwijk gold aan het eind van de vorige eeuw de voorwaarde:
Door het gebruik van nieuwe technieken neemt het geluidsniveau van vliegtuigen af.
In een zekere periode nam af van dB naar dB. Toon door berekening aan dat in die periode meer dan verdubbelde.
geeft en dus .
geeft en dus .
is ruim maal zo veel als .
Bereken de maximale waarde van waarbij er een half miljoen () vliegtuigen mogen passeren.
geeft en daaruit volgt .
In 2001 werd een nieuwe milieuwet van kracht. Voor het gebied in de buurt van vliegveld Zuidwijk geldt sindsdien:
De oude en de nieuwe formule leverden in 2001 dezelfde waarde van op.
Bereken welke waarde in 2001 had.
De waarde van geeft bij beide voorwaarden dezelfde waarde van , dus . Deze vergelijking heeft als oplossing .
In de jaren vijftig deed de Amerikaan D.L. Gerlough onderzoek naar de voetgangersveiligheid van wegen.
Als er veel verkeer over een weg gaat, is er voor voetgangers weinig gelegenheid om veilig over te steken.
Daarom stelde Gerlough de zogenaamde "veilige norm" op. Een weg voldoet aan deze
veilige norm wanneer er zich gemiddeld elke minuut een gelegenheid voordoet om veilig
over te steken. Dat lukt alleen als het aantal auto’s dat per uur passeert onder een maximum
blijft.
Dit maximum wordt genoemd en hangt af van de breedte van de
weg. Bij een brede weg duurt het oversteken langer dan bij een smalle weg. Voor wegen die
voldoen aan de veilige norm, betekent dit dat er bij een brede weg per uur minder auto’s
mogen passeren dan bij een smalle weg. Gerlough kwam tot de volgende formule:
.
Hierin is de breedte van de weg in meters.
Vanzelfsprekend is deze formule een model van de werkelijkheid. Met behulp van dit model kun je enig inzicht krijgen in de veiligheid bij de aanleg van wegen.
Bekijk de formule van Gerlough voor het maximale aantal passerende auto's om voetgangers de gelegenheid te geven veilig over te steken.
Een weg is meter breed. Tijdens de spits passeren er auto’s per uur.
Voldoet deze weg aan de veilige norm? Licht je antwoord toe.
geeft .
De weg voldoet niet aan de veilige norm.
De formule van Gerlough heeft alleen betekenis als positief is.
Bereken voor welke waarden van dit het geval is. Geef je antwoord in centimeters nauwkeurig.
als , dus als .
Dit betekent m.
De formule van Gerlough heeft betekenis voor wegen van meer dan tot maximaal m.
Een weg waarover volgens de veilige norm per uur maximaal auto’s mogen passeren, wordt meter smaller gemaakt. Dit heeft tot gevolg dat het maximum aantal auto’s dat per uur mag passeren groter wordt.
Bereken hoeveel auto’s er per uur méér mogen passeren in de nieuwe situatie.
kun je alleen oplossen met een grafische rekenmachine of GeoGebra.
Je moet dan wel flink uitzoomen om de grafieken van en in beeld te krijgen. Ga na dat je vindt.
Bij vind je .
Het maximale aantal auto's neemt met toe.
Een logaritmische functie is gegeven door .
Maak de grafiek van deze functie.
Gebruik GeoGebra, Desmos of een grafische rekenmachine.
Welke verticale asymptoot heeft de grafiek?
De -as.
Los op: .
.
geeft , dus .
Grafiek: .
Het verband tussen de (gemiddelde) lengte in cm en het (gemiddelde) gewicht in kg voor kinderen tussen en jaar wordt gegeven door de formule
De constanten en hangen af van de leefomstandigheden. Voor de westerse wereld geldt (in één decimaal nauwkeurig).
Mark (8 jaar) en Helen (10 jaar) wonen in Nederland en zijn wat lengte en gewicht betreft gemiddelde Nederlandse kinderen.
Mark heeft een lengte van m en weegt kg. Bereken in gehelen nauwkeurig.
.
geeft .
Helen is m lang. Schat haar gewicht in kg.
kg.
geeft . Dus en hieruit volgt kg.