met logaritmische schalen en logaritmisch grafiekenpapier te werken;

de formule van een exponentiële functie op te stellen vanaf enkellogaritmisch papier.

werken met exponentiële en logaritmische functies, ook met GeoGebra of een grafische rekenmachine;

werken met logaritmen en enkele eigenschappen ervan;

vergelijkingen met exponentiële en logaritmische functies oplossen.

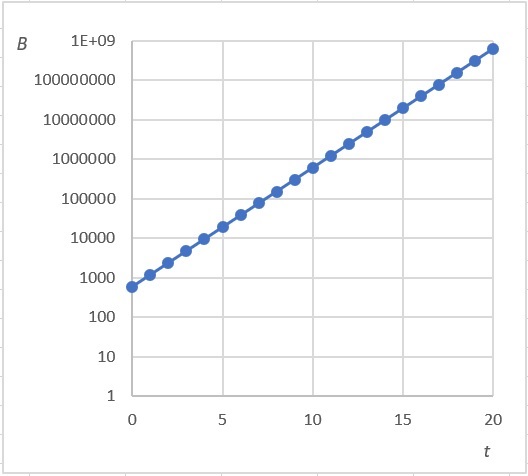
Bij bacteriegroei in een petrischaaltje kan het verloop van het geschatte aantal bacteriën $B$ worden gegeven door de formule $B = 600 * 2^t$ met $t$ in uren en $t = 0$ om 12:00 uur.
Hier zie je een grafiek van $B$ als functie van $t$ . Op de verticale as is een bijzondere schaalverdeling gebruikt.

Wat is er voor bijzonders aan die schaalverdeling?

De schaalverdeling op de verticale as loopt niet gelijkmatig op: tussen $1$ en $10$ zit evenveel afstand als tussen $10$ en $100$ .

Teken zelf eens zo'n schaalverdeling op de verticale as en maak de grafiek van $B$ als functie van $t$ .

Maak eerst een tabel met minstens vier uitkomsten. Zet op de verticale as de getallen af op de manier van de gegeven figuur. De grafiek moet een rechte lijn worden.

Als je de getallen $1$ , $10$ , $100$ en $1000$ op een getallenlijn wilt zetten, zie je dat de kleinere getallen erg dicht bij elkaar liggen en niet te onderscheiden zijn.

In plaats van een lineaire schaalverdeling zoals $0, 1, 2, 3, 4, ...$ , kun je dan een schaalverdeling met machten van $10$ : $10^0, 10^1, 10^2, 10^3, 10^4, ...$ gebruiken. Dit heet een logaritmische schaalverdeling.

Bekijk de grafiek. Op de $B$ -as is zo'n schaalverdeling gebruikt. Dit is de grafiek van een bacteriegroei. Het verloop van het aantal bacteriën $B$ in gram wordt gegeven door de exponentiële formule:
$B = 6*2^t$ met $t$ in uren en $t = 0$ om 12:00 uur.

Het getal dat je in de grafiek wilt zetten, moet dus worden vertaald naar een macht van $10$ . Daarvoor neem je de 10-logaritme van het getal. Bijvoorbeeld:

Op $t = 12$ zijn er $B = 6 * 2^12 = 24576$ bacteriën.

$log (24576) ≈ 4,39$ dus $24576$ kun je schrijven als $10^(4,39)$ .

Dan kun je het getal in het logaritmische assenstelsel zetten.

Door de horizontale hulplijnen in het assenstelsel is deze omrekening niet meer nodig.
Je weet dat $24576$ tussen $10^4=10000$ en $10^5=100000$ komt te liggen.
De eerste lijn boven $10^4$ stelt $2*10^4 = 20000$ voor.
De tweede lijn boven $10^4$ stelt $3*10^4 = 30000$ voor.
Het getal $24576$ ligt tussen deze lijntjes in (recht boven $t=12$ ).

Gebruik je op de verticale as een logaritmische schaal en op de horizontale as een lineaire schaal, dan wordt de grafiek van een exponentiële functie een rechte lijn.

Er bestaat voor dit soort grafieken speciaal enkellogaritmisch papier. Ook in Excel kun je gemakkelijk grafieken met een logaritmische schaal maken.

In de Uitleg is een grafiek van de exponentiële functie $B = 6 * 2^t$ getekend. Op de $B$ -as is een logaritmische schaalverdeling gebruikt.

Laat zien dat de punten die horen bij $t=5$ en $t=10$ goed zijn getekend.

Bij $t=5$ hoort $B = 192$ en bij $t=10$ hoort $B (10) = 6144$

$log(192) ≈ 2,3$ : je kunt $192$ schrijven als $10^(2,3)$ . Dit klopt met de positie in de grafiek.

$log(6144) ≈ 3,8$ : je kunt $6144$ schrijven als $10^(3,8)$ . Dit klopt met de positie in de grafiek.

De tweede horizontale lijn boven $10^2$ stelt $300$ voor. Laat zien dat dit op de juiste hoogte is getekend.

$log(300) ≈ 2,5$ : je kunt $300$ schrijven als $10^(2,5)$ . Dit klopt met de positie in de grafiek.

Maak een tabel voor $B$ uitgezet tegen $t$ .
Teken daarmee zelf de grafiek op enkellogaritmisch papier.

$t$	$0$	$1$	$2$	$3$	$4$	$5$	...	$15$
$B$	$6$	$12$	$24$	$48$	$96$	$192$	...	$196608$

Teken nu de grafiek op enkellogaritmisch papier. Laat het resultaat door je docent controleren!

Gegeven is de functie $y = 2 * 3^x$ .

Teken op enkellogaritmisch papier een bijpassende grafiek. Neem $0 le x le 7$ .

Maak eerst een tabel.

$x$	0	1	2	3	4	5	6	7
$y$	2	6	18	54	162	486	1458	4374

Lees uit de laatste grafiek af hoe groot de $y$ -waarde bij $x = 5,5$ is en controleer het antwoord met de gegeven formule.

Lees af: $y ≈ 840$
Als je $x = 5,5$ invult krijg je: $y = 2*3^(5,5) ~~ 841,8$ .

Bij een logaritmische schaalverdeling plaats je machten van $10$ op gelijke afstanden van elkaar. Je kunt dan zowel heel kleine als heel grote getallen plaatsen. Met behulp van de knop logaritme op de rekenmachine kun je snel vinden welke macht van 10 bij een bepaald getal hoort.

$log(1250) ≈ 3,10$
Je plaatst $1250$ op $3,10$ eenheden boven $10^0$ , dat is tussen $10^3$ en $10^4$ .

$log(0,074) ≈ text(-)1,13$
Je plaatst $0,074$ op $1,13$ eenheden onder $10^0$ , dat is tussen $10^(text(-)1)$ en $10^(text(-)2)$ .

Gebruik je op de verticale as een logaritmische schaal en op de horizontale as een gewone lineaire schaal, dan wordt de grafiek van een exponentiële functie een rechte lijn. Er bestaat speciaal enkellogaritmisch papier dat bestaat uit een as met een logaritmische schaalverdeling.

Omdat een rechte lijn op enkellogaritmisch papier de grafiek is van een exponentiële functie, kun je dat papier gebruiken om na te gaan of er tussen twee variabelen een exponentieel verband bestaat. Bij de grafiek kun je in dat geval een bijpassende formule opstellen.

Zet op de logaritmische schaal de getallen $7250$ en $0,002$ uit. Lees ook af welke waarden $a$ en $b$ hebben.

Reken eerst de getallen $7250$ en $0,002$ om.

$log(7250) ≈ 3,86$ en hieruit volgt $7250 ≈ 10^(3,86)$
Plaats $7250$ op $3,86$ eenheden boven $10^0$ , dat is tussen $10^3$ en $10^4$ .

$log ( 0,002 ) ≈ text(-)2,70$ en hieruit volgt $0,002 ≈ 10^(text(-)2,70)$
Plaats $0,002$ op $2,70$ eenheden onder $10^0$ , dat is tussen $10^(text(-)2)$ en $10^(text(-)3)$ .

Lees nu af:

$a ≈ 10^(1,5) ≈ 32$

$b ≈ 10^(text(-)0,9) ≈ 0,13$

Lees het getal $a$ op deze logaritmische schaal af.

$a$ ligt tussen $10^1$ en $10^2$ in.

Benader $a$ met $a ~~ 10^(1,8)~~63$ .

Teken een logaritmische schaal met waarden van $10^(text(-)6)$ tot $10^7$ .

Geef de getallen $20$ , $20000$ en $0,02$ op deze schaal aan.

Een mens is ongeveer $1,80$ meter groot. Geef dit getal op je schaalverdeling aan. Neem aan dat de schaal in meters is gegeven.

Zie de figuur bij a.
$log(1,8)≈0,3$ en hieruit volgt $1,8≈10^(0,3)$

De Mount Everest is ongeveer $8884$ meter hoog. Geef dit getal op je schaalverdeling aan.

Zie de figuur bij a.
$log(8884)≈3,9$ en hieruit volgt $8884≈10^(3,9)$

Een amoebe is een ééncellig organisme met een afmeting van $0,003$ tot $0,8$ millimeter. Geef deze getallen op je schaalverdeling aan.

Zie de figuur bij a.

$0,003$ mm $=0,000003$ m en $0,8$ mm $=0,0008$ m

$log(0,000003)≈text(-)5,5$ en hieruit volgt $0,000003 ≈10^( text(-)5,5)$

$log(0,0008)≈text(-)3,1$ en hieruit volgt $0,0008≈10^( text(-)3,1)$

Op de schaalverdeling is $a$ het getal dat midden tussen $10^3$ en $10^4$ in zit. Bereken $a$ in gehelen.

$a = 10^(3,5) ≈ 3162,3$

Jodium-131 is een onstabiele radioactieve en zeer gevaarlijke stof. Jodium-131 komt van nature niet op aarde voor, maar is wel vrijgekomen tijdens de kernrampen in Tsjernobyl en Fukushima. Ook wordt Jodium-131 geproduceerd in een kernreactor om het te kunnen gebruiken in de nucleaire geneeskunde ter behandeling van onder andere schildklierkanker. Jodium-131 heeft als eigenschap dat het vervalt, er verwijnt steeds een beetje van de stof.
Bekijk de vervaltabel van Jodium-131.

tijd (dagen)	$0$	$2$	$4$	$6$	$8$	$10$	$12$	$14$	$16$
hoeveelheid ( $mu$ g)	$400$	$336$	$282$	$238$	$202$	$166$	$142$	$116$	$98$

Teken bij deze tabel een grafiek op enkellogaritmisch papier en onderzoek of er sprake is van exponentiële groei (verval).

$400=4*10^2$ ; het eerste punt komt bij het derde streepje boven $10^2$ .
$336=3,36*10^2$
$282=2,82*10^2$
$238=2,38*10^2$
$202=2,02*10^2$
$166=1,66*10^2$
$142=1,42*10^2$
$116=1,16*10^2$
$98=9,8*10^1$

Er is sprake van exponentiële groei, want de punten van de grafiek liggen (bij benadering) op een rechte lijn.

Bekijk de twee vervaltabellen met daarin de hoeveelheid $M$ van stof M en de hoeveelheid $P$ van stof P in microgram ( $mu$ g).

tijd (h)	1	4	16	64
M (mug)	1000	250	62,5	15,6

tijd (h)	0	24	48	72
P (mug)	1000	250	62,5	15,6

Onderzoek met behulp van grafieken op enkellogaritmisch papier of er sprake is van exponentiële groei.

De punten van stof $P$ vormen een rechte lijn op enkellogaritmisch papier, de punten van stof $M$ niet. Bij stof $P$ is er sprake van exponentiële groei en bij stof $M$ niet.

$1000=10^3$
$250=2,5*10^2$
$62,5=6,25*10^1$
$15,6=1,56*10^1$

De punten van stof $P$ vormen een rechte lijn op enkellogaritmisch papier, de punten van stof $M$ niet. Bij stof $P$ is er sprake van exponentiële groei en bij stof $M$ niet.

Maak een assenstelsel met op de verticale as een logaritmische schaalverdeling, of gebruik enkellogaritmisch papier. Gegeven is nu de functie $N = 12000 * 0,8^t$ .

Teken de grafiek van $N$ in het assenstelsel of op het enkellogaritmische papier.

Als het goed is krijg je een rechte lijn.

Maak een tabel met een aantal punten.

$t$	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$
$N$	$12000$	$9600$	$7680$	$6144$	$4915,2$	$3932,2$	$3145,7$	$2516,6$	$2013,3$

Als het goed is krijg je een rechte lijn.

Lees uit de figuur de waarden van $t$ af waarvoor $N lt 3000$ .
Geef je antwoord in één decimaal nauwkeurig.

$t gt 6,2$ .

Bekijk de grafiek van de groei van een waterplant.
De oppervlakte $A$ (m2) is een functie van de tijd $t$ (weken). Stel een bijpassende formule op.

De grafiek is een rechte lijn met alleen op de verticale as een logaritmische schaal. Er bestaat daarom een exponentieel verband tussen $A$ en $t$ : $A = b * g^t$

Lees uit de figuur af:

bij $t = 0$ hoort $A ≈ 6*10^1 ≈ 60$ .

bij $t = 8$ hoort $A ≈ 9*10^2 ≈ 900$ .

De groeifactor per $8$ weken is ongeveer $900/60$ .

De groeifactor per week is ongeveer: $(900/60)^(1/8) ≈ 1,4$

De formule is: $A ≈ 60*1,4^t$

In Voorbeeld zie je een rechte lijn in een assenstelsel waarvan de verticale as een logaritmische schaal heeft. Daarbij kun je een functievoorschrift opstellen van de vorm $A = b*g^t$ .

Lees de waarden af voor $A$ bij $t = 5$ en $t = 7$ .

$A (5) ≈ 3*10^2 ≈ 300$
$A (7) ≈ 6*10^2 ≈ 600$

Stel met behulp van deze waarden een formule voor $A$ op.
Ga na dat je ongeveer dezelfde formule vindt als in het voorbeeld.

$A(t) = b*g^t$
$A(5) ≈ 300$
$A(7) ≈ 600$
Hieruit volgt: $g^2 ≈ 600/300 ≈ 2$ en $g ≈ 2^ (1/2) ≈ 1,4$ .

Invullen van $g~~1,4$ en $b~~60$ geeft: $A ~~ 60*1,4^t$ .

Zo vind je dezelfde formule als in het voorbeeld.

Waarom is het handiger om de waarde bij $t = 0$ te gebruiken?

Omdat deze waarde meteen de waarde van $b$ oplevert.

Bekijk deze grafiek van $N$ als functie van $t$ .

Welke coördinaten heeft het snijpunt van de horizontale en verticale as?

Op de $y$ -as staan de machten van $10$ , bij de oorsprong staat $y=10^0=1$ .

Op de $x$ -as staan getallen zoals je gewend bent, zodat bij de oorsprong $x=0$ .

Het snijpunt is $(0, 10^0) = (0, 1)$ .

Lees twee waarden voor $N$ uit de grafiek af en stel een formule op voor $N$ .

Lees de punten $(text(-)4, 1000)$ en $(5; 0,01)$ af.

Bij $x=text(-)4$ is $N = b * g^(text(-)4) = 1000$ .
Bij $x=5$ is $N = b * g^5 = 0,01$ .
Hieruit volgt: $g^9 = (0,01)/1000 = 0,00001$ zodat $g = 0,00001^ (1/9) ≈ 0,28$ .
Invullen geeft: $b ≈ 5,99$ .

De formule is: $N ≈ 6 * 0,28^t$ .

Bereken ter controle met de formule van b het snijpunt met de getekende $t$ -as.

$N = 1$ geeft $0,28^t ≈ 0,167$ en hieruit volgt $t ≈ \ ^{:0,28:} log (0,167) ≈ 1,41$ .
Het snijpunt wordt ongeveer $(1,41; 1)$ .

Waarom heeft het geen nut om te vragen naar de $t$ -waarden waarvoor $N = 0$ ?

Op de verticale as komt het getal $0$ helemaal niet voor.
Op de verticale as staan de getallen $..., 10^(text(-)3), 10^(text(-)2), 10^(text(-)1), 10^0, 10^1, 10^2, 10^3, ...$
Dat zijn allemaal positieve getallen, dus $N gt 0$ .

De bevolking van een middelgrote stad groeit vanaf 1 januari 2010 met (ongeveer) $6$ % per jaar. Op 1 januari 2010 zijn er $80000$ inwoners.

Stel een formule op voor het aantal inwoners $A$ afhankelijk van de tijd $t$ in jaren vanaf 1 januari 2010.

$A = 80000 * 1,06^t$

Teken een bijpassende grafiek op enkellogaritmisch papier.

$t$	$0$	$2$	$4$	$6$	$8$	$10$
$A$	$80000$	$89888$	$100998$	$113482$	$127508$	$143268$
$log(A)$	$4,90$	$4,95$	$5,00$	$5,05$	$5,11$	$5,16$

$log(A)$ hoef je alleen te berekenen als je geen enkellogaritmisch papier hebt en zelf een logaritmische schaalverdeling maakt.

Lees uit die grafiek het aantal inwoners af op 1 januari 2025. Controleer je antwoord met behulp van de formule.

Schatting: ongeveer $190000$ .
De formule geeft: $A = 80000*1,06^(15) ≈ 191725$ .

Bekijk de tabel die bij gegevens over een bacteriecultuur hoort.
$t$ is gegeven in uren en $N$ in aantallen.

$t$	$0$	$1$	$2$	$3$	$4$	$5$	$6$
$N$	$50$	$84$	$141$	$237$	$398$	$670$	$1125$

Maak met behulp van de gegeven tabel een grafiek $N$ uitgezet tegen $t$ op enkellogaritmisch papier. Is er sprake van exponentiële groei?

Je krijgt ongeveer een rechte lijn door $(0; 1,70)$ en $(4; 2,60)$ .
Omdat de grafiek van $N$ bij benadering een rechte lijn is, is $N$ bij benadering een exponentiële functie.

Stel een formule op voor $N$ als functie van $t$ .

Bij $t=0$ is $N = b*g^0 = 50$ , dus $b=50$ .

Bij $t=6$ is $N = 50*g^6 = 1125$ , dus $g^6 = 22,5$ en $g = 22,5^(1/6) ~~ 1,68$ .

De formule wordt $N = 50 * 1,68^t$ .

Bereken $N$ als $t = 10$ uur.

Bij $t=10$ is $N = 50*1,68^10 ~~ 8955$ bacteriën.

Op enkellogaritmisch papier is de grafiek getekend van een toenemende hoeveelheid $V$ als functie van de tijd $t$ .

Geef een formule voor $V$ .

Bij $t=0$ is $V = b*g^0 = 2$ , dus $b=2$ .

Bij $t=5$ is $V = 2*g^5 = 6$ , dus $g^5 = 3$ en $g = 3^(1/5) ~~ 1,25$ .

De formule wordt $V = 2 * 1,25^t$ .

Bereken in twee decimalen de waarde van $t$ waarvoor $V = 10$ . Controleer je antwoord met de grafiek.

$V = 10$ geeft $1,25^t = 5$ en hieruit volgt $t = \ ^{:1,25:} log(5) ≈ 7,21$ .
Ga na, dat dit klopt met de grafiek.

De grafiek lijkt op het enkellogpapier een snijpunt met de $t$ -as te hebben.
Bereken de bijbehorende waarde van $t$ in twee decimalen.

$V = 1$ geeft $1,25^t = 0,5$ en hieruit volgt $t = \ ^{:1,25:} log (0,5) ≈ text(-)3,11$ .

Op enkellogaritmisch papier is de grafiek getekend van een afnemende hoeveelheid $A$ als functie van de tijd $t$ .

Geef een formule voor $A$ .

Bij $t=0$ is $A = b*g^0 = 400$ , dus $b=400$ .

Bij $t=8$ is $A = 400*g^8 = 7$ , dus $g^8 = 7/400$ en $g = (7/400)^(1/8) ~~ 0,60$ .

De formule wordt $A = 400 * 0,60^t$ .

Bereken in twee decimalen de waarde van $t$ waarvoor $A = 20$ . Controleer je antwoord met de grafiek.

$A = 20$ geeft $400*0,60^t = 20$ en hieruit volgt $0,60^t=0,05$ . Dit geeft $t = \ ^{:0,60:} log(0,05) ≈ 5,86$ .

Controleer dit in de grafiek door te bedenken dat $20=2*10^1$ . Kijk langs de verticale as bij het eerste blauwe streepje boven $10^1$ . Daar hoort inderdaad $t~~5,86$ bij.

De grafiek lijkt op het enkellogpapier een snijpunt met de $t$ -as te hebben. Bereken de bijbehorende waarde van $t$ in twee decimalen.

$A = 1$ geeft $400*0,60^t = 1$ en hieruit volgt $0,60^t=1/400$ . Dit geeft $t = \ ^{:0,60:} log(1/400) ≈ 11,73$ .

Honing bestaat grotendeels uit vocht en suikers en voor een klein gedeelte uit andere stoffen, zoals enzymen en mineralen. De kwaliteit van honing hangt onder andere af van de concentratie van het enzym diastase: hoe meer diastase, hoe beter de kwaliteit van de honing. De concentratie van diastase in honing wordt aangeduid met het diastasegetal.

Door het bewaren van honing gaat er diastase verloren en neemt dus het diastasegetal af. De snelheid waarmee dat gebeurt, hangt af van de temperatuur waarbij de honing wordt bewaard. Een maat waarmee de afname van het diastasegetal kan worden weergegeven, is de zogeheten halfwaardetijd. Dat is de tijd waarin het diastasegetal wordt gehalveerd. Bekijk de grafiek waarin deze halfwaardetijd is uitgezet tegen de temperatuur waarbij de honing wordt bewaard.

Wat is beter: honing bewaren bij een lage temperatuur of bij een hoge temperatuur? Licht je antwoord toe en maak daarbij gebruik van de grafiek.

Uit de grafiek blijkt dat een hogere temperatuur een lagere halfwaardetijd geeft. Een lagere halfwaardetijd geeft een snellere afname van het diastasegetal. De honing kan dus beter bij een lage temperatuur worden bewaard.

Het diastasegetal is bij de meeste soorten honing direct na winning niet hoger dan $30$ .
Als het diastasegetal lager is dan $8$ , mag de honing alleen nog maar als bakkershoning worden verkocht.
Een bepaald type honing heeft bij winning een diastasegetal van $28$ .
Deze honing wordt gedurende drie jaar bewaard bij een temperatuur van $25$ °C.
Ga ervan uit dat de afname van het diastasegetal exponentieel verloopt.

Laat met behulp van de grafiek zien dat deze honing na drie jaar bakkershoning is geworden.

Bij $25$ °C is de halfwaardetijd ongeveer $500$ dagen: $500$ dagen= $500/365≈1,37$ jaar.

Voor de groeifactor per jaar geldt nu $g^(1,37)=1/2$ geeft $g ≈ 0,603$ .

Per drie jaar is dat $0,603^3 ~~ 0,219$ en het diastasegetal is dan $28*0,219=6,136$ . Na drie jaar is de honing bakkershoning.

Soms versuikert honing. Er ontstaan dan suikerkorrels op de bodem van een pot honing.
Versuikerde honing wordt weer vloeibaar door de honing te verhitten.
Uit de grafiek blijkt dat het diastasegetal wordt gehalveerd als honing $24$ uur lang op een temperatuur van $60$ °C wordt gehouden.
Een partij honing met een diastasegetal van $27$ wordt gedurende een bepaalde tijd op een temperatuur van $60$ °C gehouden. Ga er nog steeds van uit dat de afname van het diastasegetal exponentieel verloopt.

Bereken hoelang het duurt totdat deze partij bakkershoning is geworden.

De groeifactor per uur is $0,5^(1/24) ~~ 0,972$ .
Los op: $27*0,972^t = 8$ .
Het antwoord is ongeveer $42$ uur (of $43$ uur).

Zoogdieren gaan bij een bepaalde pasfrequentie (het aantal passen per minuut) over van draf naar galop. De pasfrequentie waarbij dat gebeurt hangt af van de lichaamsmassa.
Noem de lichaamsmassa $m$ (in kilogram) en de pasfrequentie $P$ .
De rechte lijn gaat door de punten die horen bij een kleine hond en bij paarden.
Op beide assen is nu een logaritmische schaal gebruikt.

Daardoor hoort bij deze rechte lijn een formule van de vorm $log(P) = a*log(m)+b$ .

Dit kun je herleiden tot $P = 10^b * m^a$ , zodat $P$ een machtsfunctie is van $m$ .

Bekijk de grafiek van de pasfrequentie $P$ afhankelijk van de lichaamsmassa $m$ in kg.

Waar kun je aan zien dat op beide assen van deze grafiek een logaritmische schaal is gebruikt?

Bij de maatstreepjes staan machten van $10$ .

Welke pasfrequentie en welke lichaamsmassa horen bij kleine hond?

$m ≈ 10^(0,1) ~~ 1,26$ kg.
$P ≈ 10^(2,4) ~~ 251$ passen per minuut.

Welke pasfrequentie en welke lichaamsmassa horen bij paard?

$m ≈ 10^(2,9) ~~ 795$ kg.
$P ≈ 10^(2) = 100$ passen per minuut.

De grafiek in toepassen kan worden benaderd met de formule $P = 259*m^(text(-)0,14)$ .

Laat zien dat de waarden die je in de vorige opgave hebt afgelezen voor kleine hond en paard hieraan voldoen.

Bij kleine hond hoort $m ~~ 1,26$ kg en $P ~~ 251$ passen per minuut.
Vul dit in de formule in

Bij paard hoort $m ~~ 795$ kg en $P ~~ 100$ passen per minuut.
Vul dit in de formule in.

Het gewicht van een savanneolifant is gemiddeld $6000$ kg.
Bij welke pasfrequentie gaat deze olifant van draf naar galop?

$P = 259*6000^(text(-)0,14) ~~ 77$ passen per minuut.

Teken een getallenlijn met een logaritmische schaalverdeling (neem deze figuur over).

Welk getal hoort bij het pijltje?

$10^(1,1) ≈ 12,59$

Teken een pijltje dat hoort bij het getal $2$ .

Zie figuur bij a.

Geef aan waar $5,5$ en waar $10^(0,5)$ moeten staan. Doe dit ook bij $55$ en $10^(1,5)$ .

Zie figuur bij a.

Geef ook $3 1/4$ en $10^(1/4)$ aan.

Zie figuur bij a.

Bij een biologisch experiment groeit in een vijver een waterplant. De waterplant bedekt een steeds groter deel van het wateroppervlak. Elke week meet men de oppervlakte die de waterplant bedekt. De meetwaarden staan in de tabel.

aantal weken	$0$	$1$	$2$	$3$	$4$	$5$	$6$
oppervlakte (dm2)	$40$	$57$	$89$	$134$	$200$	$305$	$447$

Zet de punten $( 0 , 40 ) , ( 1 , 57 ) , ... , ( 6 , 447 )$ uit op enkellogaritmisch papier.

Doen.

Trek door deze punten zo goed mogelijk een rechte lijn.

De punten liggen ongeveer op een rechte lijn door $( 0 , 40 )$ en $( 4 , 200 )$ .

Van welk type groei is hier sprake? Waar zie je dat aan?

Punten liggen ongeveer op een rechte lijn, dus exponentiële groei.

Stel een formule op voor de oppervlakte $A$ die de waterplant bedekt, afhankelijk van de tijd $t$ in weken.

$A = 40 * 1,495^t$ met $t$ in weken.

Bij $t=0$ is $A = b*g^0 = 40$ , dus $b=40$ .

Bij $t=4$ is $A = 40*g^4 = 200$ , dus $g^4 = 5$ en $g = 5^(1/4) ~~ 1,495$ .

De formule wordt $A = 40 * 1,495^t$ .