In dit onderwerp heb je gewerkt met periodieke verschijnselen en ontdekt dat functies met sinus en cosinus standaard periodieke functies zijn. Daarbij hoort het werken met radialen in plaats van graden. Verder zijn de begrippen periode, frequentie, evenwichtsstand en amplitude voorbij gekomen. Deze zijn vaak goed te gebruiken bij het beschrijven van periodieke verschijnselen.
Je hebt nu alle theorie van
Reken de hoeken in graden om naar radialen tussen en , en omgekeerd. Rond zo nodig af op twee decimalen.
rad
rad
rad
rad
rad
rad
rad
afgerond
rad
Bekijk een periodieke grafiek.
Voor geldt
Bepaal de periode van de grafiek.
De periode is .
Voor welke waarden van geldt ?
met een geheel getal
voor . Dit kun je ook schrijven als met een geheel getal.
Bereken als .
Bij hoort dezelfde waarde voor als bij en die is .
Bereken als .
Bij hoort dezelfde waarde voor als bij en die is .
Los de volgende vergelijkingen op. Geef je antwoorden in twee decimalen nauwkeurig.
Bij het bepalen van de gewenste dijkhoogte langs de Nederlandse kust is het
belangrijk dat de dijk hoger is dan de te verwachten maximale waterhoogte
bij een stormvloed. De gemiddelde waterhoogte is daarbij niet van belang.
Bij normale omstandigheden kan de getijdenbeweging van het zeewater bij de
Hondsbosse Zeewering te Petten redelijk worden beschreven door de functie:
Hierin is in uur ten opzichte van middernacht op 21 juni
1998 en de waterhoogte in meter ten opzichte van het NAP. Onder
invloed van de stand van de zon en de maan kan de amplitude van de
getijdenbeweging variëren van % tot % van de amplitude van de gegeven
functie. Afhankelijk van de windsterkte kan de gemiddelde waterhoogte bij
aanlandige wind tot meter hoger zijn dan normaal.
Hoe hoog moet de zeedijk van Petten minimaal zijn? Licht je antwoord toe.
De amplitude van de grafiek van de gegeven functie is . De amplitude van de getijdenbeweging varieert van tot m.
De gemiddelde waterhoogte onder normale omstandigheden is m. De gemiddelde hoogte onder niet-normale omstandigheden is m.
De dijk zou minimaal een hoogte van m moeten hebben.
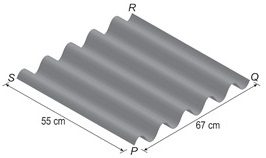
Golfplaat is een bouwmateriaal dat gebruikt wordt voor het afdekken van eenvoudige bouwwerken. In de figuur hiernaast is een rechthoekig stuk golfplaat getekend. Hieronder is het vooraanzicht van dit stuk golfplaat in een assenstelsel getekend. Hierbij is de dikte verwaarloosd. In het assenstelsel zijn en uitgedrukt in cm. Bij deze grafiek behoort de formule:
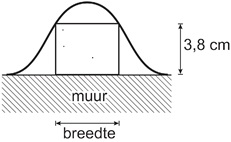
De golfplaat wordt als afdakje gebruikt. De plaat wordt horizontaal neergelegd en steunt aan de randen en op een muur. De ruimtes tussen de bovenrand van de muur en de golfplaat worden afgedicht met houten blokjes. Deze blokjes zijn cm hoog en hebben een zo groot mogelijke breedte. In de figuur hiernaast is dit geschetst.

Bereken de breedte van zo'n blokje. Geef je antwoord in mm nauwkeurig.
geeft . De breedte van het blokje is ongeveer cm en dat is ongeveer mm.
Het bovenaanzicht van het stuk golfplaat (zie de figuur rechtsboven) is een rechthoek . cm en cm. Dit stuk golfplaat wordt diagonaal doorgezaagd. In het bovenaanzicht is de zaagsnede een rechte lijn van naar . De werkelijke vorm van de doorsnede is een sinusoïde.
Stel een formule op van deze sinusoïde als deze op ware grootte in een assenstelsel zoals in het vooraanzicht wordt weergegeven.
De amplitude van de sinusoïde is . Van P naar Q is perioden en van S naar Q is ook perioden. . De periode van de gevraagde sinusoïde is ongeveer cm. Een passende formule is .
(bron: examen wiskunde B1,2 havo 2005, tweede tijdvak, opgave 5)

In 1610 werden de vier helderste Jupitermanen ontdekt door Galileï. De manen beschrijven bij benadering cirkelvormige banen om Jupiter, alle vier in dezelfde omlooprichting. Deze banen liggen (vrijwel) in één vlak met Jupiter en de aarde. Daarom zie je Jupiter en de vier manen in een kijker altijd op één horizontale lijn liggen. De onderlinge posities van de manen in het kijkerbeeld veranderen voortdurend. Voor amateurastronomen worden maandelijks grafieken gepubliceerd waaruit ze op ieder moment de posities van de manen kunnen aflezen. Zie hemel.waarnemen.com: Galileïsche manen van Jupiter, slingerdiagram september 2008 Het diagram op de website geeft informatie over de maand september in 2008. Deze slingerdiagrammen zijn vrijwel zuivere sinusoïden.
Voor Ganymedes bijvoorbeeld wordt deze harmonische beweging goed beschreven door waarin de tijd in dagen is met op 1 sep 2008 om 0:00 uur en de uitwijking t.o.v. Jupiter gemeten in Jupiterstralen.
Zo kun je ook van de beweging van de drie andere Galileïsche manen een formule opstellen. En verder kun je op elk moment tekenen hoe je deze manen t.o.v. Jupiter vanaf Aarde ziet. Nog een leuke puzzel...
Op september 2008 om 0:00 uur waren dus van links (west) naar rechts (oost) in de kijker te zien: Io (I, voor Jupiter), Europa (II), Ganymedes (III) en Callisto (IV). Hier zie je van de vier manen de posities op hun cirkelbanen op januari 1990 om 0:00 uur getekend.
Bekijk de gegevens van de Jupitermanen.
Teken in de figuur voor deze vier manen het deel van de baan dat ze doorlopen van 1 september 0:00 uur tot 5 september 0:00 uur.
Doen.
De diameter van Jupiter is ongeveer km.
Hoe ver is Ganymedes gemiddeld van Jupiter verwijderd?
De amplitude van zijn baan is Jupiterstralen.
Ganymedes is dus Jupiterstralen van de planeet verwijderd, dat is ongeveer km.
Hoeveel dagen doet Ganymedes over één omwenteling rond Jupiter?
dagen.
In de kijker zie je de beweging van elk van die manen als een in de tijd veranderende uitwijking ten opzichte van Jupiter op een horizontale as. Die uitwijking kan goed worden beschreven met een sinusoïde. wordt uitgedrukt in veelvouden van de straal van Jupiter en is in dagen. Voor Callisto geldt bij goede benadering . (Hierbij is er van uit gegaan dat
Laat zien dat deze formule redelijk overeenkomt met de grafiek in het slingerdiagram van september 2008.
Bereken met de formule de omlooptijd van Callisto.
Maak zelf de grafiek. Omlooptijd Callisto is dagen.
Stel zo'n formule op voor de Jupitermaan Europa.
Amplitude en periode dagen. Eerste periode start op .
Europa: .
De manen zijn in de figuur naar verhouding veel te groot getekend. In werkelijkheid zijn het stipjes. Dus als dan kunnen de manen achter Jupiter zitten.
Bereken met behulp van de formule voor Ganymedes hoe lang deze maan achter Jupiter zit.
Ganymedes zit achter Jupiter als hij van west naar oost beweegt en . geeft . geeft . Ganymedes gaat achter Jupiter op bijvoorbeeld en komt er dan weer achter weg op . Ganymedes zit dus ongeveer dagen achter Jupiter.