aanzichten gebruiken bij berekeningen in ruimtelijke figuren.

de verschillende ruimtelijke basisfiguren;

gelijkvormigheid, de stelling van Pythagoras en goniometrie toepassen in ruimtelijke figuren.

Dit zijn drie aanzichten van een lichaam.

Om wat voor lichaam gaat het hier? Maak er een uitslag van en beschrijf de daarvoor noodzakelijke berekeningen.

Dit is een halve balk $A B C D . E F$ met als grondvlak rechthoek $A B C D$ met $A B = 10$ en $B C = 6$ cm. Zie verder de figuur.

Je moet wel $A E$ berekenen met de stelling van Pythagoras: $A E = \sqrt{10^{2} + 6^{2}} = \sqrt{136} \approx 11,7$ cm.

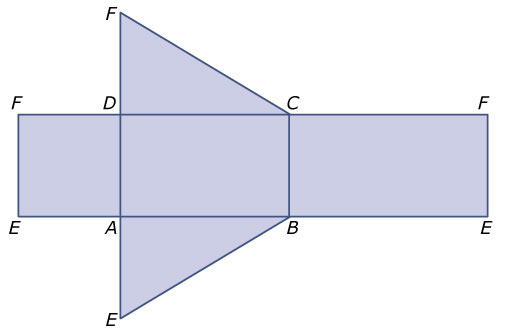
Dit is het regelmatige zeszijdige prisma $A B C D E F . G H I J K L$ . In zo'n regelmatig lichaam zijn veel ribben en diagonalen gelijk aan elkaar. Toch blijkt daar in de figuur niet zoveel van. Als je zou gaan meten zijn $A B$ , $B C$ en $C D$ zeker niet gelijk, dat komt door de tekening in parallelprojectie. In een parallelprojectie worden alleen even lange lijnstukken die evenwijdig lopen ook weer even lang.

Soms helpt het om dan aanzichten van een lichaam te gebruiken. Een drieaanzicht zoals dat hieronder laat het vooraanzicht, het zijaanzicht en het bovenaanzicht van het lichaam zien. Daarin zie je allerlei grensvlakken in de juiste vorm en op ware grootte.

Bekijk de Uitleg. Je ziet er een regelmatig zeszijdig prisma. Neem aan dat van het grondvlak alle zijden $4$ cm zijn en dat de opstaande ribben allemaal $6$ cm lang zijn. Op het werkblad bij deze opgave zie je de aanzichten van het prisma met enkele hoekpunten erbij aangegeven.

Het vooraanzicht is $6$ cm hoog. Hoe breed is de totale breedte van het vooraanzicht?

$8$ cm, namelijk de lengte van (bijvoorbeeld) $C F$ . (Denk aan het voorgaande onderdeel, of kijk nog even terug als je niet meer weet waarom $C F = 8$ cm.)

Het zijaanzicht is ook $6$ cm hoog. Hoe breed is de totale breedte van het zijaanzicht?

$4 \sqrt{3}$ cm, namelijk de lengte van (bijvoorbeeld) $B D$ . (Denk aan het voorgaande onderdeel, of kijk nog even terug als je niet meer weet waarom $B D = 3 \sqrt{3}$ cm.)

In welk aanzicht is een opstaand grensvlak op ware grootte getekend?

Alleen in het vooraanzicht.

Zet bij de aanzichten op het werkblad de letters op de juiste plek bij de hoekpunten.

Teken in de aanzichten het diagonaalvlak $B E K H$ .

Werkblad bij opgave

Het lichaam hiernaast is een regelmatige zeszijdige piramide $A B C D E F . T$ . Alle zijden van het grondvlak zijn $4$ cm. Alle opstaande ribben zijn $12$ cm.

Bereken de hoogte van deze piramide.

Neem aan, dat $S$ het midden is van de cirkel door de hoekpunten van het grondvlak. Dan kun je in $Δ A S T$ de stelling van Pythagoras toepassen.
$S T = \sqrt{12^{2} - 4^{2}} = \sqrt{128} \approx 11,3$ cm.

Teken een vooraanzicht, een zijaanzicht en een bovenaanzicht van deze piramide op schaal $1 : 2$ .

Zet de letters van de hoekpunten op de goede plaats in de aanzichten.

Welke opstaande ribben worden op ware grootte weergegeven? En in welk aanzicht?

Alleen de ribben $A T$ en $D T$ in het vooraanzicht.

Geef het getekende diagonaalvlak in de aanzichten weer.

Je ziet hier een drieaanzicht van een lichaam. De figuur staat ook op een werkblad.

Om wat voor lichaam gaat het hier?

Om een regelmatig driezijdig prisma.

Bij het zijaanzicht ontbreekt een afmeting. Hoe groot moet de hoogte ervan zijn?

De hoogte van het vooraanzicht is hetzelfde als de hoogte van het zijaanzicht.
In het vooraanzicht kun je die hoogte uitrekenen: $\sqrt{6^{2} - 3^{2}} = \sqrt{27} \approx 5,2$ .

De figuur krijgt de naam $ABE.DCF$ . Zet in de aanzichten de letters bij de juiste hoekpunten.

Werkblad bij opgave

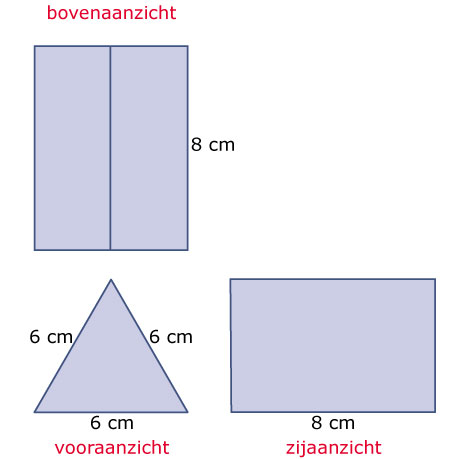
Je ziet hier een regelmatig driezijdig prisma $A B E . D C F$ . Dit lichaam is getekend als parallelprojectie.
Dit betekent dat evenwijdige lijnen ook evenwijdig worden getekend en dat lijnstukken die evenwijdig en even lang zijn ook evenwijdig en even lang worden.

Maar er is ook een drieaanzicht van getekend. Dat is een combinatie van een vooraanzicht, een bovenaanzicht en een zijaanzicht. In aanzichten zie je meestal veel afmetingen op ware grootte, je kunt er beter metingen in verrichten dan in een parallelprojectie. Wel is het soms lastig om op basis van aanzichten te herkennen om wat voor figuur het gaat.

Deze kartonnen doos heeft de vorm van een vijfzijdig prisma. De voorkant en de achterkant zijn symmetrische vijfhoeken met twee rechte hoeken. De afmetingen vind je bij de figuur.

Teken een drieaanzicht van deze doos.

Van het bovenaanzicht weet je alle afmetingen, dus dat kun je meteen tekenen. Van het vooraanzicht weet je ook alle afmetingen en als je dan van de symmetrie gebruik maakt en de passer gebruikt voor de twee zijden van $4$ dm, dan kun je ook dat tekenen. Het zijaanzicht vind je door vooraanzicht en bovenaanzicht te combineren.

In Voorbeeld wordt een drieaanzicht van een doos getekend.

Teken dit drieaanzicht zelf op schaal $1 : 20$ .

Doen. Lees in het voorbeeld na hoe het vooraanzicht wordt getekend.

De figuur is een prisma $A B C D E . F G H I J$ . Hierin is vijfhoek $A B C D E$ het voorvlak, met $A B = B C = 6$ dm en $A E = 4$ dm.

Zet de letters in je drieaanzicht op de juiste plek.

Bereken nu de hoogte van de voorkant van de doos, dus de hoogte van punt $E$ boven lijn $B C$ in mm nauwkeurig.

$M$ is het midden van $A D$ .
Gebruik de stelling van Pythagoras in $Δ A M E$ .
De gevraagde hoogte wordt $\sqrt{4^{2} - 3^{2}} + 6 = 6 + \sqrt{7} \approx 8,65$ cm.

Bereken de grootte van $/_ AED$ in graden nauwkeurig.

$sin(/_ AEM) = 3/4 = 0,75$ zodat $/_ AEM ~~ 48,6^@$ en $/_ AED ~~ 97,2^@ ~~ 97^@$ .

Van een regelmatige vierzijdige piramide $A B C D . T$ zijn alle ribben $4$ cm.

Teken een drieaanzicht van deze piramide.

Doen. Het bovenaanzicht is een vierkant van $4$ bij $4$ cm met daarin de twee diagonalen getekend als aanzicht van de vier ribben van de piramide. Voor het vooraanzicht en het zijaanzicht moet je (bijvoorbeeld) eerst de hoogte $T S$ van de piramide berekenen waarin $S$ het snijpunt van $A C$ en $B D$ is. Ga na dat $T S = \sqrt{8}$ .

Zet de letters op de juiste plek bij de aanzichten. Laat je antwoord even controleren.

Je ziet hier het bovenaanzicht en het zijaanzicht van een veelvlak. Welk veelvlak betreft het en hoe groot is de totale oppervlakte van dat lichaam?

Dit betreft een vierzijdige piramide $A B C D . T$ met een rechthoekig grondvlak.
Voor de totale oppervlakte van dit lichaam moet je de oppervlakte van het grondvlak en van de vier opstaande grensvlakken bij elkaar optellen.

De grensvlakken $A B T$ en $C D T$ zijn twee congruente gelijkbenige driehoeken met een basis van $8$ cm en een hoogte die je in het zijaanzicht op ware grootte ziet. Die hoogte is dus $\sqrt{6^{2} - 3^{2}} = 3 \sqrt{3}$ cm. De oppervlakte van elk van deze twee grensvlakken is $\frac{1}{2} \cdot 8 \cdot 3 \sqrt{3} = 12 \sqrt{3}$ cm.

De grensvlakken $B C T$ en $D A T$ zijn twee congruente gelijkbenige driehoeken met een basis van $6$ cm en een hoogte die je in het vooraanzicht op ware grootte ziet. Die hoogte is dus $\sqrt{6^{2} - 4^{2}} = 2 \sqrt{5}$ cm. De oppervlakte van elk van deze twee grensvlakken is $\frac{1}{2} \cdot 6 \cdot 2 \sqrt{5} = 6 \sqrt{5}$ cm.

Nu kun je de totale oppervlakte wel berekenen...

In Voorbeeld zie je twee aanzichten van een lichaam.

Hoe ziet het vooraanzicht van dit lichaam er uit? En waarom weet je dat zeker?

Een gelijkbenige driehoek met een basis van $8$ cm en een hoogte van $6$ cm. Dat kan niet anders omdat het lichaam een veelvlak is en er dus geen gebogen grensvlakken zijn.

Waarom is de hoogte van het vooraanzicht niet gelijk aan de hoogte van de driehoek $A B T$ ? Laat zien hoe je daarvan de hoogte berekend.

Dat staat in het voorbeeld. Merk nog op dat je die hoogte in het zijaanzicht kunt zien! Het is de linker van de twee gelijke benen van het zijaanzicht. Als je daar dan een hoogtelijn vanuit $T$ in tekent, dan kun je de hoogte van $Δ A B T$ berekenen met de stelling van Pythagoras.

Bereken de totale oppervlakte van dit lichaam, zowel exact als in mm2 nauwkeurig.

De totale oppervlakte is $8 * 6 + 2 * 1/2 * 6 * sqrt(52) + 2 * 1/2 * 8 * sqrt(73) ~~ 159,6$ cm2.

Van een veelvlak is het bovenaanzicht een gelijkzijdige driehoek met zijden van $4$ cm en het vooraanzicht een vierkant met zijden van $4$ cm.

Welk veelvlak is dit? Bereken er de totale oppervlakte van.

Dit is een regelmatig driezijdig prisma.

Alle drie de opstaande grensvlakken zijn vierkanten met een oppervlakte van $4 \cdot 4 = 16$ cm2.
De twee gelijkzijdige driehoeken hebben een oppervlakte van $\frac{1}{2} \cdot 4 \cdot 2 \sqrt{3} = 4 \sqrt{3}$ cm2.
De totale oppervlakte is dus $48 + 8 \sqrt{3}$ cm2.

Over het eind van een buis wordt ter afsluiting een kegelvormig kapje geplaatst. Dit wordt gemaakt van buigbare kunststof.
Een zijaanzicht ervan zie je hiernaast, alle afmetingen zijn in mm.
Teken nu zelf een uitslag van deze kegel.

Elke kegel kun je vouwen uit een deel van een cirkel, een cirkelsector.
De straal van die cirkelsector is dan gelijk aan de lengte van een lijnstuk vanuit de top naar de grondcirkel. Die lengte bereken je met de stelling van Pythagoras: $R = sqrt(300^2 + 120^2) ~~ 323$ mm.

Je begint daarom met een cirkel met een straal van $323$ mm.
Daar heb je maar een deel van nodig.
De boog die bij dat deel hoort moet even lang zijn als de grondcirkel van de kegel, dus $pi*600$ mm.
De cirkel die je hebt getekend heeft een omtrek van $pi*646$ mm.
Dus van de $360^@$ die bij een complete cirkel horen, heb je $(pi*600)/(pi*646)*360^@ ~~ 334^@$ nodig.
Dit heet de sectorhoek van de cirkelsector.

Teken de uitslag van de kegel beschreven in Voorbeeld op schaal $1:10$ .
Maak je tekening op stevig papier en maak een extra plakrand. Vouw de kegelvorm en ga na dat hij klopt met de opgegeven afmetingen.

Maak de figuur zoals die in het voorbeeld, maar nu correct op schaal.

Meet na het vouwen van de kegel zowel de diameter van de grondcirkel als de hoogte na.
Controleer dat je ongeveer uitkomt op de opgegeven maten. (Denk aan de schaal!)

Je ziet hier het zijaanzicht van een lampekap met de vorm van een afgeknotte kegel.

Teken een uitslag van deze afgeknotte kegel.

De grondcirkel heeft een diameter van $4$ dm en de topcirkel een diameter van $2$ dm. Dat is gemakkelijk te tekenen.

Omtrek grondcirkel: $2*pi*2=4pi$

De cirkel waar de kegelmantel deel van is, heeft een straal van $6$ dm, dus de omtrek van deze cirkel is: $2*pi*6=12pi$ . De sectorhoek wordt dan $4/12*360^@=120^@$ . Denk er bij het tekenen aan dat de kegel afgeknot is.

Je ziet hier een piramide $A B C . T$ waarvan het grondvlak $A B C$ een gelijkzijdige driehoek met zijden van $6$ cm is. De top $T$ ligt recht boven het midden $M$ van ribbe $A C$ . De ribben $A T$ en $C T$ zijn allebei $5$ cm lang.

Teken een vooraanzicht, een zijaanzicht en een bovenaanzicht van deze piramide.

Zie figuur. Bereken eerst $M T = \sqrt{5^{2} - 3^{2}} = 4$ .

Bereken de lengte van ribbe $B T$ .

Eerst bereken je $M B = \sqrt{6^{2} - 3^{2}} = 3 \sqrt{3}$ .
En dan is $B T = \sqrt{{(3 \sqrt{3})}^{2} + 4^{2}} = \sqrt{43}$ cm.

Bereken de grootte van $/_ MTB$ in graden nauwkeurig.

$sin(/_ MTB) = 5/(sqrt(43))$ geeft $/_ MTB ~~ 50^@$ .

Een veelvlak $A B C . D E F$ heeft als vooraanzicht een vierkant met zijden van $4$ cm en als zijaanzicht een gelijkbenige driehoek waarvan de basis ook $4$ cm is.

Teken het bovenaanzicht van dit veelvlak en bereken de oppervlakte van het veelvlak.

Het bovenaanzicht is een vierkant $A B E D$ met zijden van $4$ cm. Lijnstuk $F C$ verbindt de middens van $D E$ en $A B$ .

Omdat $A C = B C = \sqrt{2^{2} + 4^{2}} = \sqrt{20} = 2 \sqrt{5}$ is de totale oppervlakte $4 \cdot 4 + 2 \cdot 4 \cdot 2 \sqrt{5} + 2 \cdot \frac{1}{2} \cdot 4 \cdot 4 = 32 + 16 \sqrt{5}$ .

In het beeldenpark in Zwijndrecht staan verschillende beelden. Eén van die beelden is het beeld op de foto hieronder. De onderkant van het beeld dat op de sokkel staat, is een vierkant met zijden van $50$ cm. Het beeld is $100$ cm hoog en de lengte van de bovenkant is $100$ cm lang. Het vooraanzicht en het zijaanzicht zijn symmetrisch.

Teken een bovenaanzicht van dit beeld op schaal $1 : 10$ .

Teken eerst een vierkant van $5$ bij $5$ cm. Verbind dan de middens van de onderste en de bovenste zijde en laat deze lijn aan beide zijden $2,5$ cm uitsteken. Je krijgt dan deze figuur.

Het grondvlak van dit beeld is een vierkant $A B C D$ . De bovenkant is een ribbe $E F$ . In het vooraanzicht zie je de punten $A$ , $B$ en $E$ .

Bereken de lengte van ribbe $B E$ in mm nauwkeurig.

Maak een schets van de figuur met de letters op de juiste plek. Neem aan dat $P$ het midden van $A B$ is en dat $Q$ op $E F$ ligt met $E Q = 25$ cm.

Je weet dan dat $P Q = 100$ cm, de hoogte van het beeld.
Verder is $B Q = \sqrt{100^{2} + 25^{2}} = \sqrt{10625}$ . Daaruit volgt dat $B E = \sqrt{10625 + 25^{2}} = \sqrt{11250} \approx 106,1$ cm.

Als het beeld in de verf zou worden gezet, hoeveel cm2 verf is daar dan voor nodig?

Het grondvlak hoeft niet, daar staat het beeld op. Het gaat daarom om de trapeziums $B C E F$ en $D A E F$ en de gelijkbenige driehoeken $A B E$ en $C D F$ .

Beide gelijkbenige driehoeken hebben een basis van $50$ cm en een hoogte van $P E = \sqrt{100^{2} + 25^{2}} = \sqrt{10625}$ . Hun oppervlakte is $25 \sqrt{10625}$ .

De oppervlakte van één van beide trapeziums is $\frac{1}{2} \cdot (100 + 50) \cdot \sqrt{10625} = 75 \sqrt{10625}$ .

De totale oppervlakte is daarom $200 \sqrt{10625} \approx 20616$ cm2.

Op de foto hieronder zie je kinderen spelen op een speeltoestel. Het speeltoestel is een constructie van metalen buizen waarin een net is gespannen. Op de tekening ernaast zie je de metalen constructie die bestaat uit vier even grote ruiten. Elke zijde van zo’n ruit is $3$ meter lang. Elk van die ruiten heeft bij het punt op de grond een hoek van $60^@$ . Alle verticale stippellijnen staan loodrecht op vierkant $A B C D$ .

Teken een bovenaanzicht van de metalen constructie op schaal $1 : 10$ .

Merk eerst op dat $FG = 3$ m omdat $Delta BGF$ gelijkzijdig is.
Noem $F'$ het midden van $AB$ en $G'$ het midden van $BC$ .
Dan is $F'G' = FG$ en dus is $AC = 2*F'G'= 6$ .
Vierkant $ABCD$ heeft daarom zijden van $sqrt(18)$ cm.
Teken dat vierkant en verbind de middens van de overstaande zijden.

Bereken hoe hoog punt $T$ boven de grond zit, dus de lengte van $T S$ in cm nauwkeurig.

Bekijk $Delta ACT$ . Daarvan is $AC = sqrt(18)$ en $AT = CT = sqrt(27)$ .

En dus is $TS = sqrt((sqrt(27))^2 - (0,5sqrt(18))^2) = sqrt(22,5)$ .

Bereken de grootte van $/_ AFB$ .

Bekijk $Delta AFB$ . Daarvan is $AF = BF = 3$ en $AB = sqrt(18)$ .

En dus is $sin(/_ AFF') = (0,5sqrt(18))/3$ zodat $/_ AFB = 90^@$ .

Dit is een model van een achtkantig symmetrisch lichaam waarvan het grondvlak een vierkant $A B C D$ is met zijden van $8$ cm en ook het bovenvlak $E F G H$ een vierkant is. Alle opstaande grensvlakken zijn gelijkbenige driehoeken met ribben van $6$ cm.

Van deze achtkanter liggen alle hoekpunten van het bovenvlak recht boven de middens van de zijden van het grondvlak. Dat maakt alle aanzichten eenvoudig...

Bereken de zijden van het bovenvlak $E F G H$ .

Alle zijden zijn $4 sqrt(2)$ cm.

Bereken de hoeken van $Δ B G F$ .

$cos(/_ BFG) = (2 sqrt(2))/6$ geeft $/_BFG ~~ 62^@$ .
Vanwege de symmetrie is $/_BGF ~~ 62^@$ en $/_GBF ~~ 56^@$ .

Teken een drieaanzicht van deze achtkanter. Zet de letters van de hoekpunten op de juiste plaats in je figuur.

Zie figuur.

Stel je voor dat deze achtkanter massief zou zijn en moet worden geverfd. Hoe groot bedraagt dan zijn totale buitenoppervlakte?

$8 * 8 + 4sqrt(2)*4sqrt(2) + 4 * 1/2 * 8 * sqrt(20) + 4 * 1/2 * 4sqrt(2)*sqrt(28) ~~ 227,42$ cm2.

De uitslag van een kegel is een kwart cirkel met een straal van $10$ cm.

Hoe groot is de diameter en hoe hoog is het driehoekige zijaanzicht van die kegel?

De omtrek van de uitgesneden kwart cirkel is $1/4*pi*20 = 5pi$ en is ook de omtrek van de onderste cirkel van de afgeknotte kegel. Die moet daarom een diameter van $5$ cm hebben.
De hoogte van het driehoekig zijaanzicht is $sqrt(10^2-2,5^2) ~~ 9,7$ cm.

Bouwtekeningen zijn tekeningen die worden gebruikt om iets te kunnen bouwen. Dat kan een kastje, een toestel, een huis, een vliegtuig of wat dan ook zijn... Vaak zijn bouwtekeningen aanzichten en plattegronden met veel details of opengewerkte tekeningen.
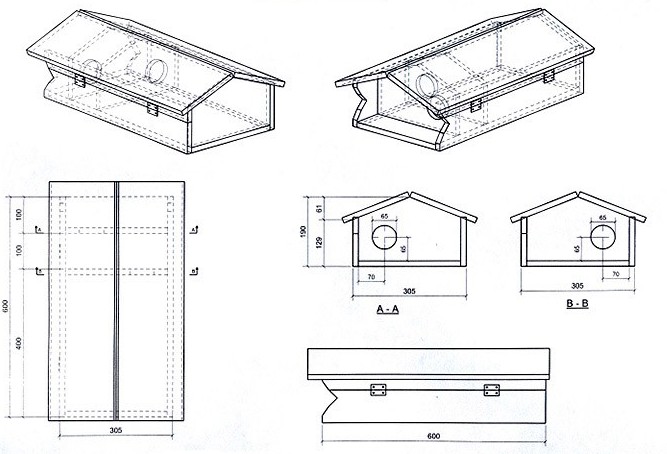
Hier zie je een bouwtekening van een nestkast voor steenuilen.

Bekijk de bouwtekening van de steenuilenkast.

In welke eenheid zijn alle afmetingen gegeven?

In millimeter.

Hoe kun je in de bouwtekening zien dat deze nestkast kan worden opengeklapt?

Er zijn scharnieren zichtbaar in het rechter zijvlak (als je van voren kijkt).

Hoe kun je zien dat deze nestkast een ingang heeft die bestaat uit twee schotten met gaten met een stuk open ruimte er tussen?

Je ziet dat in het bovenaanzicht (gestippeld) en in de twee 3D-tekeningen.
Bovendien staan er twee "vooraanzichten".

Teken zelf één zo'n schot op schaal $1 : 2$ .

Kijk goed naar de gegeven afmetingen en ook naar de plek van het invlieggat.

De twee delen van het schuine dak zijn nergens getekend. Welke vorm en afmetingen hebben die dakdelen?

Het zijn rechthoeken met een lengte van bijvoorbeeld $620$ mm (meer dan $600$ mm) en een breedte van $180$ mm (meer dan $170$ mm).

Waarom is hier het maken van een uitslag niet goed mogelijk?

Er is sprake van een tussenwand en van overstekende dakdelen.

Hier zie je een andere nestkast. Het voorvlak (met het aanvlieggat) is een rechthoek van $20$ cm bij $30$ cm. Het achtervlak is een rechthoek van $20$ cm bij $35$ cm. Het grondvlak is een vierkant. Het schuine bovenvlak is aan de voorkant $2$ cm langer dan nodig om het hokje dicht te maken. De invliegopening heeft een diameter van $6$ cm.

Maak een passend drieaanzicht op schaal $1:5$ .

Teken eerst het zijaanzicht. Uit de maten gegeven in de opgave, kun je afleiden dat het zijvlak $4$ cm breed, links $6$ cm hoog en rechts $7$ cm hoog is. Het dak is in het zijaanzicht $5$ cm lang. Teken daarna het vooraanzicht en het bovenaanzicht met behulp van het zijaanzicht . Deze aanzichten zijn $4$ cm breed. Teken stippellijnen vanuit het zijaanzicht om de hoogtematen te kunnen tekenen. Met deze hulplijnen zorg je ervoor, dat de maten van de aanzichten overeenkomen. Omdat het dak schuin loopt, zie je in het bovenaanzicht een dubbele rand.

Van een achtkantig lichaam is het grondvlak $A B C D$ een vierkant met zijden van $8$ cm en het bovenvlak $E F G H$ een vierkant met zijden van $4$ cm.
Alle zes de opstaande zijvlakken zijn gelijkbenige driehoeken met benen van $6$ cm lengte.
$F$ is het snijpunt van de diagonalen van $ABCD$ en $S$ is het snijpunt van de diagonalen van $EFGH$ .
$TS$ staat loodrecht op zowel het grondvlak als het bovenvlak.

Bereken van deze achtkanter de hoogte $T S$ in één decimaal nauwkeurig.

Dus $TS = sqrt(16sqrt(2)-4) ~~ 4,3$ cm.

In $Delta BFG$ is nu de hoogte $BK$ gelijk aan $BK = sqrt(32)=4sqrt(2)$ .
$TS$ kan worden verschoven naar $KL$ met $L$ op $BS$ . Omdat $LS = 2$ is $BL = 4sqrt(2) - 2$ .
Dus $TS = KL = sqrt((4sqrt(2))^2 - (4sqrt(2)-2)^2) = sqrt(16sqrt(2)-4)$ .

Teken een drieaanzicht van deze achtkanter. Zet weer de letters van de hoekpunten op de juiste plaats in je figuur.

Zie figuur.

Hoe groot zijn de hoeken van de opstaande zijvlakken?

Er zijn zijvlakken van $6$ , $6$ en $8$ cm als zijden.
Die hebben hoeken van $48^@$ , $48^@$ en $84^@$ .

Er zijn zijvlakken van $6$ , $6$ en $4$ cm als zijden.
Die hebben hoeken van $71^@$ , $71^@$ en $38^@$ .

Stel je voor dat deze achtkanter massief zou zijn. Hoe groot is dan zijn totale buitenoppervlakte?

$~~ 196,81$ cm2.

$8 * 8 + 4 *4 + 4 * 1/2 * 8 * sqrt(20) + 4 * 1/2 * 4 * 4sqrt(2) ~~ 196,81$ cm2.

Het zijaanzicht van een kegel is een gelijkbenige driehoek met zijden van $6$ , $6$ en $4$ dm.

Hoe ziet een uitslag van deze kegel er uit? Geef ook de belangrijke afmetingen.

Een cirkelsector met een straal van $6$ en een sectorhoek van $120^@$ .

De diameter van de kegel is $4$ cm, dus de grondcirkel heeft een lengte van $pi*4$ cm.

De cirkelsector (die de uitslag voorstelt) heeft een straal van $6$ cm en dus een omtrek van $pi*12$ cm. Daarvan is maar het $(pi*4)/(pi*12) = 1/3$ deel nodig, de sectorhoek is daarom $120^@$ .

De kegel wordt geschilderd, de bodem niet. Hoeveel bedraagt de buitenoppervlakte?

$~~ 37,7$ cm2.

$1/3 * pi * 6^2 ~~ 37,7$ cm2.