het begrip kruisende lijnen;

een doorsnede van een ruimtelijke figuur met een vlak herkennen en op ware grootte tekenen;

doorsneden gebruiken bij berekeningen in ruimtelijke figuren.

de verschillende ruimtelijke basisfiguren;

gelijkvormigheid, de stelling van Pythagoras en goniometrie toepassen in ruimtelijke figuren;

aanzichten gebruiken bij berekeningen in ruimtelijke figuren.

Je ziet hier en op het werkblad vier kubussen met ribben van $2$ cm. Joop heeft geprobeerd om in elke kubus te laten zien hoe een bepaald plat vlak de kubus doorsnijdt.

Welke tekeningen zijn dan fout? En waarom?

De figuren I en IV zijn fout. De punten van deze vierhoeken op de ribben van de kubus liggen niet in een plat vlak maar op een gebogen oppervlak. Pak er eventueel een draadmodel van een kubus bij en maak daarin de figuren door touwtjes te spannen. Alleen als het mogelijk is om alle touwtjes precies achter elkaar te zien als je de kubus in een geschikte stand houdt, liggen ze allemaal in één plat vlak.

Verbeter de foute figuren.

Dat kan op verschillende manieren.

Welke vorm heeft de doorsnede van figuur II in werkelijkheid? En welke afmetingen?

Die doorsnede is een rechthoek van $2$ cm bij $\sqrt{2^{2} + 1^{2}} = \sqrt{5}$ cm.

Werkblad bij opgave

Je ziet hiernaast de doorsnede $A P G Q$ van een plat vlak met een kubus getekend. De kubus heeft ribben van $5$ cm. $P$ en $Q$ zijn de middens van de ribben waarop ze liggen.

Als je de kubus in de richting $B D$ bekijkt zie je $A$ , $P$ , $G$ en $Q$ op één lijn liggen. En daarom weet je zeker dat ze in één vlak liggen. Je kunt het ook zo zien: de snijlijnen in twee overstaande evenwijdige grensvlakken van de kubus (bijvoorbeeld $A P$ en $Q C$ ) zijn evenwijdig en dus is $A P G Q$ een plat vlak. Bedenk dat lijnen die in één vlak liggen elkaar altijd snijden of evenwijdig lopen. Lijnen die elkaar niet snijden èn niet evenwijdig lopen noem je kruisende lijnen. In een vlak kunnen nooit kruisende lijnen liggen! En daarom kan de vierhoek $A P G H$ nooit een vierhoek in een plat vlak zijn: de lijnstukken $A H$ en $P G$ zijn niet evenwijdig en liggen dus op kruisende lijnen.

Als je $A P G Q$ op ware grootte wilt zien moet je de kubus zo draaien dat je loodrecht op dat vlak kijkt. Je ziet dan dat $A P G Q$ een ruit is met ribben van $\sqrt{5^{2} + {2,5}^{2}} = \sqrt{31,25}$ cm en een diagonaal $P Q$ van $\sqrt{50}$ cm. Je tekent hem zelf op ware grootte door eerst $P Q$ te tekenen en dan de zijden vanuit $P$ en $Q$ om te cirkelen.

Bekijk de kubussen in de Uitleg. Je ziet dat in de bovenste kubus een vlak $A P G Q$ is getekend.

Teken het aanzicht van de bovenste kubus waarbij je kijkt in de richting van $B D$ met het vlak $A P G Q$ er in. Waaraan zie je dat $A P G Q$ een plat vlak is?

Dan ligt diagonaalvlak $A C G E$ recht voor je en dat is een rechthoek van $\sqrt{50} = 5 \sqrt{2}$ bij $5$ . In de figuur zie je nu de punten $A$ , $P$ , $G$ en $Q$ op één lijn liggen.

Kun je van de onderste kubus een aanzicht tekenen waarbij de punten $A$ , $P$ , $G$ en $H$ op één lijn liggen?

Nee, dat is onmogelijk.

Waarom zijn de zijden van $A P G Q$ in twee overstaande vlakken van de kubus evenwijdig? En waarom zijn ze dus ook gelijk?

Ze zijn allemaal zijden van een rechthoekige driehoek van $5$ bij $2,5$ cm waarvan de langste rechthoekszijde horizontaal (evenwijdig met het grondvlak van de kubus) is. En daarom zijn ze ook even lang.

Teken de doorsnede $A P G Q$ op ware grootte.

Begin met diagonaal $P Q$ . Deze diagonaal heeft een lengte van $\sqrt{50}$ cm. Daarna cirkel je vanuit punt $P$ de zijden $P A$ en $P G$ om en vanuit punt $Q$ cirkel je $Q A$ en $Q G$ om. Nu kun je de ruit afmaken.

Bereken de lengte van diagonaal $A G$ .

Dat kan in de ruit die je zojuist bij d hebt getekend, of in het diagonaalvlak $A C G E$ . In beide gevallen heb je de stelling van Pythagoras nodig: $A G = \sqrt{75} = 5 \sqrt{3}$ .

In de Uitleg wordt gesproken over kruisende lijnen.

Waarom zijn de lijnen $A H$ en $P G$ kruisend?

Ze zijn niet evenwijdig. Verder liggen ze in vlakken die evenwijdig zijn, dus kunnen ze elkaar ook niet snijden (al lijkt dat misschien als je de lijnstukken $A H$ en $P G$ langer maakt wel zo te zijn).

Zijn de lijnen $A P$ en $H G$ kruisend, of snijdend? (Denk er om dat deze lijnen ook buiten de lijnstukken $A P$ en $H G$ doorlopen.)

Ze zijn kruisend. Want ze liggen in twee verschillende evenwijdige vlakken en lopen niet evenwijdig.

Zijn de lijnen $A P$ en $E F$ kruisend, of snijdend?

De lijnen zijn snijdend want ze liggen beide in het voorvlak van de kubus.

In kubus $A B C D . E F G H$ met ribben van $6$ cm is vierhoek $K C G L$ een doorsnede van een plat vlak met de kubus. Punt $K$ is het midden van ribbe $A B$ .

Waarom is driehoek $K C G$ geen complete doorsnede van een vlak met deze kubus?

Er zijn punten buiten deze driehoek die zowel op het vlak door die drie punten als binnen of op de kubus liggen.

Waarom moet punt $L$ het midden van ribbe $E F$ zijn?

Omdat lijnstuk $K L$ evenwijdig moet zijn met ribbe $C G$ .

Teken de doorsnede $K C G L$ op ware grootte.

De doorsnede is een rechthoek met lengte $K C$ en breedte $C G$ . De lengte van $K C$ bereken je met de stelling van Pythagoras: $K C = \sqrt{3^{2} + 6^{2}} = \sqrt{45}$ cm.

Een doorsnede van een ruimtelijke figuur met een plat vlak is de figuur die wordt gevormd door alle snijlijnen. Heeft die doorsnede de vorm van een driehoek, dan kun je ervan verzekerd zijn dat het inderdaad om een plat vlak gaat.
Bij vierhoeken, vijfhoeken, etc., moet je nauwkeuriger kijken.
Om te controleren dat zo'n figuur echt vlak is, kun je gebruiken dat in een plat vlak alleen evenwijdige of elkaar snijdende lijnen liggen. Lijnen die niet evenwijdig zijn èn elkaar niet snijden heten kruisende lijnen. Lijnen die elkaar kruisen kunnen nooit in één vlak liggen.

Om in een doorsnede berekeningen te kunnen uitvoeren teken je hem op ware grootte.
Daarmee wordt bedoeld dat alle hoeken hun werkelijke vorm hebben en alle zijden hun werkelijke lengte (eventueel op schaal getekend). Bij het tekenen op ware grootte construeer je vaak driehoeken met behulp van de passer. Teken hulpfiguren (vaak rechthoekige driehoeken) waarvan je de afmetingen al kent om onbekende lengten en hoeken te vinden.

Je ziet hier een balk $A B C D . E F G H$ . Gegeven is $A B = 6$ , $B C = 3$ , $C G = 4$ . De punten $P$ en $Q$ zijn de middens van de ribben waarop ze liggen.
Waarom is vierhoek $DPQG$ een doorsnede van een plat vlak met de gegeven balk?
Teken doorsnede $D P Q G$ op ware grootte.

Vierhoek $DPQG$ is een doorsnede van een plat vlak met de gegeven balk omdat de lijnen $PQ$ en $DG$ evenwijdig lopen.

De lengte van $D G$ kun je halen uit rechthoekige $Δ D C G$ : $D G = \sqrt{45}$ .

De lengte van $D P$ kun je halen uit rechthoekige $Δ D A P$ : $D P = \sqrt{18}$ .

Omdat $B Q = 2$ kun je de lengtes van $P Q$ en $Q G$ ook berekenen: $P Q = Q G = \sqrt{13}$ .

Om het trapezium $DPQG$ te kunnen tekenen, is het handig om eerst nog de lengte van een diagonaal te berekenen, bijvoorbeeld $P G = \sqrt{34}$ . Nu kun je de figuur construeren door twee driehoeken te maken met passer en liniaal.

In Voorbeeld is een doorsnede van een plat vlak met een balk getekend. Je wilt die doorsnede op ware grootte tekenen.

Waarom zijn de lijnen $PQ$ en $DG$ evenwijdig?

De lijn $DG$ is hypothenusa van een rechthoekige driehoek met rechthoekszijden $DC=6$ en $CG=4$ .
De lijn $PQ$ is hypothenusa van een rechthoekige driehoek met rechthoekszijden $PB=3$ en $BQ=2$ .
Beide lijnen liggen in evenwijdige vlakken (voorvlak en achtervlak van de balk) en de driehoeken $DCG$ en $PBQ$ zijn gelijkvormig.

Bereken de lengte van $D G$ en die van $D P$ .

Doen, gebruik de stelling van Pythagoras. Het antwoord staat in het voorbeeld.

Reken nu de lengtes van $P Q$ en $Q G$ na.

Doen, gebruik de stelling van Pythagoras en eventueel de gelijkvormigheid.

Bereken de lengte van diagonaal $P G$ .

Doen, gebruik de stelling van Pythagoras in $Δ P C G$ .

Teken trapezium $DPQG$ op ware grootte.

Teken eerst $Δ D G P$ (daarvan weet je alle zijden) en zet daar $Δ P G Q$ op.

Gegeven is balk $A B C D . E F G H$ met $A B = 6$ cm, $B C = 4$ cm en $B F = 5$ cm. $M$ is het midden van $A E$ , $N$ is het midden van $C G$ .

Er worden nu steeds twee lijnen gegeven. Schrijf op of ze elkaar snijden, evenwijdig zijn of elkaar kruisen.

$M H$ en $B N$ .

Evenwijdige lijnen.

$M B$ en $H C$ .

Kruisende lijnen.

$A E$ en $H G$ .

Kruisende lijnen.

$M F$ en $A B$ .

Snijdende lijnen.

$M N$ en $H B$ .

Snijdende lijnen.

$C M$ en $A F$ .

Kruisende lijnen.

Gegeven is balk $A B C D . E F G H$ met $A B = 6$ cm, $B C = 4$ cm en $B F = 5$ cm. $M$ is het midden van $A E$ , $N$ is het midden van $C G$ en $K$ ligt op $B F$ met $B K = 1$ cm.

Is $H M K N$ een doorsnede van een vlak met deze balk? Licht je antwoord toe.

Nee, want bijvoorbeeld $M K$ en $H N$ zijn niet evenwijdig.

Is $K E G$ een doorsnede van een vlak met deze balk? Licht je antwoord toe.

Ja, van deze driehoek liggen alle zijden op de grensvlakken van de balk.

Is $K M N$ een doorsnede van een vlak met deze balk? Licht je antwoord toe.

Nee, van deze driehoek liggen maar twee zijden op de grensvlakken van de balk, de andere zijde niet. Er zijn dus nog punten van het vlak door $K$ , $M$ en $N$ die binnen of op de balk en buiten de gegeven driehoek liggen.

Vierhoek $H M B N$ is een doorsnede van een vlak met de gegeven balk.

Teken deze vierhoek op ware grootte. Schrijf alle noodzakelijke berekeningen op.

$M B = \sqrt{6^{2} + {2,5}^{2}} = \sqrt{42,25} = 6,5$ en $B N = \sqrt{4^{2} + {2,5}^{2}} = \sqrt{22,25} \approx 4,7$ .
Verder is diagonaal $M N = \sqrt{6^{2} + 4^{2}} = \sqrt{52} \approx 7,2$ .
Nu kun je eerst $Δ M B N$ tekenen. Maar omdat $M H = B N$ en $H N = M B$ kun je $Δ M H N$ daar tegenaan tekenen.

Hier zie je een regelmatig driezijdig prisma $A B C . D E F$ waarvan alle zijden $8$ cm lang zijn. De punten $P$ , $K$ , $L$ , $M$ en $N$ zijn steeds de middens van de ribben waar ze op liggen.

Waarom is vierhoek $K L M N$ de doorsnede van een vlak met dit prisma?

De lijnstukken $K L$ en $M N$ liggen op evenwijdige lijnen en de andere twee zijden van de vierhoek snijden deze beide lijnen.

Teken vierhoek $K L M N$ op ware grootte. Schrijf alle daarvoor noodzakelijke berekeningen op.

$M N = 8$ en $K L = 4$ cm (vanwege de gelijkvormigheid van de driehoeken $K B L$ en $A B C$ ). Verder is $N K = L M = \sqrt{4^{2} + 4^{2}} = 4 \sqrt{2}$ .
$K L M N$ is een gelijkbenig trapezium. In de figuur zie je hoe je het nu kunt tekenen.

Bereken (als je dat bij b nog niet hebt gedaan) alle hoeken van vierhoek $K L M N$ in graden nauwkeurig.

In de figuur bij b zie je dat $cos(/_ NML) = 2/(4sqrt(2))$ zodat $/_ NML ~~ 69^@$ .
De vierhoek heeft dus twee hoeken van ongeveer $69^@$ en twee van ongeveer $111^@$ .

Deze tekening stelt een tent voor. De afmetingen zijn in de figuur gegeven. Ga er van uit dat de lichter gekleurde stippellijnen in een snijpunt loodrecht op elkaar staan.

$GH$ is de nok van de tent.
Om de hoek die de vlakken $CDHG$ en $FAGH$ met elkaar maken te bepalen moet je in een vlak kijken waar hun snijlijn loodrecht op staat. Die hoek heet de standhoek van beide vlakken. Je kunt hem zien in een vooraanzicht van de tent, maar ook in de doorsnede $Delta ACG$ .
Bereken de standhoek van de vlakken $CDHG$ en $FAGH$ .

De gevraagde hoek is $/_ AGC$ .

Omdat $tan(/_ AGT) = 1/(1,5)$ is $/_ AGT ~~ 33,7^@$ .
Dus is $/_ AGC ~~ 2*33,7^@ ~~ 67^@$ .

Bekijk het berekenen van de standhoek van de vlakken $CDHG$ en $FAGH$ in Voorbeeld.

Bereken zelf de standhoek van de vlakken $BCG$ en het grondvlak $ABCDEF$ .

$P$ is het midden van $BC$ . De standhoek is dan $/_TPG$ .

Omdat $TP = BT = TC = 1/2 * sqrt(1^2+1^2) = 1/2 sqrt(2)$ is $tan(/_TPG) = (1,5)/(1/2 sqrt(2))$ en dus $/_TPG ~~ 64,8^@$ .

Je ziet hier in balk $A B C D . E F G H$ twee keer een figuur getekend die vier hoekpunten heeft.

Leg uit bij welke van beide figuren er sprake is van de doorsnede van een plat vlak en de getekende balk. Licht je antwoord toe.

Alleen in de rechter figuur is daarvan sprake.
De lijnen $B Q$ en $G H$ in de linkerfiguur zijn kruisende lijnen, dus kunnen die lijnen nooit in één vlak liggen. In de rechter figuur zijn de lijnen $C H$ en $P Q$ evenwijdig (vanwege de gelijkvormigheid van de driehoeken $A P Q$ en $D C H$ , waardoor de hoeken van beide driehoeken gelijk zijn).

Je ziet hier een balk $A B C D . E F G H$ met daarin de punten $P$ , $Q$ en $R$ die alle drie het midden van een ribbe van de balk vormen.

Schrijf van de volgende lijnen op of ze elkaar snijden, elkaar kruisen, of evenwijdig zijn. Licht je antwoord toe.

$P Q$ en $B F$ .

Kruisend, deze lijnen liggen niet in één vlak.

$P Q$ en $R G$ .

Snijdend, deze lijnen liggen in vlak $P C G R$ .

$P R$ en $G H$ .

Kruisend, deze lijnen liggen niet in één vlak.

$R G$ en $P C$ .

Evenwijdig en deze lijnen liggen in vlak $P C G R$ .

$P C$ en $A D$ .

Snijdend, deze lijnen liggen in vlak $A B C D$ .

Van de regelmatige vierzijdige piramide $A B C D . T$ is punt $P$ het midden van ribbe $C T$ en punt $Q$ het midden van ribbe $D T$ . Verder is gegeven dat $A B = B C = 8$ cm en $A T = 12$ cm.

Bereken de lengte van lijnstuk $B P$ .

$Δ B C T$ is een gelijkbenige driehoek met hoogte $T M = \sqrt{12^{2} - 4^{2}} = \sqrt{128} = 8 \sqrt{2}$ . Als $N$ het midden is van $M C$ , dan is $Δ B N P$ rechthoekig met rechthoekszijden $B N = 6$ en $N P = 4 \sqrt{2}$ (gebruik de gelijkvormigheid van de driehoeken $N C P$ en $M C P$ ).
En dus is $B P = \sqrt{6^{2} + {(4 \sqrt{2})}^{2}} = \sqrt{68}$ .

Vierhoek $A B P Q$ is de doorsnede van de piramide met een vlak.

Teken deze doorsnede op ware grootte.

Vierhoek $A B P Q$ is een symmetrisch trapezium met $A B = 8$ cm, $P Q = 4$ cm en $B P = A Q = \sqrt{68}$ cm.

Bereken de hoeken van vierhoek $A B P Q$ in graden nauwkeurig.

In de figuur bij b zie je dat $cos(/_ BAQ) = 2/(sqrt(68))$ zodat $/_ BAQ ~~ 69^@$ .
De vierhoek heeft dus twee hoeken van ongeveer $76^@$ en twee van ongeveer $104^@$ .

Op de foto hieronder zie je kinderen spelen op een speeltoestel. Het speeltoestel is een constructie van metalen buizen waarin een net is gespannen. Op de tekening ernaast zie je de metalen constructie die bestaat uit vier even grote ruiten. Elke zijde van zo’n ruit is $3$ meter lang. Elk van die ruiten heeft bij het punt op de grond een hoek van $60^@$ . Alle verticale stippellijnen staan loodrecht op vierkant $A B C D$ . De vier ruiten vormen samen met de vier opstaande driehoeken en het vierkante grondvlak een lichaam.

Bereken de hoeken van dwarsdoorsnede $A C T$ van dit lichaam in graden nauwkeurig.

Je hebt (vorige onderdeel, verwerken) uitgerekend dat $AC = 3sqrt(2)$ en $AT = CT = 3sqrt(3)$ .

Dus is $cos(/_ CAT) = (1,5sqrt(2))/(3sqrt(3))$ zodat $/_ CAT ~~ 66^@$ .
Hieruit volgt $/_ ACT ~~ 66^@$ en $/_ ATC ~~ 48^@$ .

Neem aan dat $M$ het midden van $A D$ en $N$ dat van $B C$ is.

Teken de dwarsdoorsnede $M N G T E$ van dit lichaam op ware grootte.

Dit is een symmetrische vijfhoek met $MN = 3sqrt(2)$ , $ME = NG = sqrt(3^2 - (1,5sqrt(2))^2) = sqrt(4,5)$ en $TS = sqrt(22,5)$ .

Hier zie je een vereenvoudigd model van het dak van een stolpboerderij. Het dak is zuiver symmetrisch, dus de ribben $A E$ , $D E$ , $B F$ en $C F$ zijn even lang en $E F$ loopt evenwijdig met $A B$ en $C D$ .

Bereken de standhoek van de vlakken $ABFE$ en $CDEF$ .

Teken doorsnede $FPQ$ met $P$ op $AB$ met $PB=3$ en $Q$ op $CD$ met $CQ=3$ . $Delta FPQ$ is een gelijkbenige driehoek met basis $PQ = 8$ en hoogte $5$ m.
De gevraagde standhoek is $/_ PFQ$ .
Omdat $tan(1/2 /_ PFQ) = 4/5$ is $/_ PFQ ~~ 77^@$ .

Waarom is $/_ BFC$ niet de standhoek van de vlakken $ABFE$ en $CDEF$ ?

Omdat vlak $BFC$ niet loodrecht op de snijlijn van $ABFE$ en $CDEF$ staat.

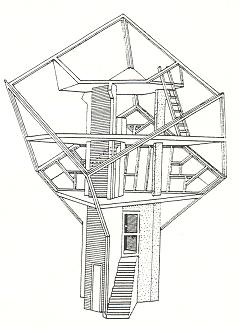
De kubuswoning ontworpen door architect Piet Blom is beroemd. In Helmond en in Rotterdam zijn van deze kubuswoningen gebouwd. Hiernaast zie je een opengewerkt model. Het betreft daar in grote lijnen een kubus die op zijn punt staat, er zitten dus twee hoekpunten die zijn verbonden met een lichaamsdiagonaal recht boven elkaar. Deze kubus staat op een brede paal waarin zich de toegang bevindt.

In de kubuswoning zitten drie vloeren, de onderste vloer is driehoekig, de middelste zeshoekig en de bovenste eigenlijk weer driehoekig, maar daar zijn opstaande driehoekige wanden gemaakt die evenwijdig lopen met vlakken van de kubus.

Bekijk het opengewerkte model van een kubuswoning. Je gaat dit model zelf tekenen met behulp van het werkblad.

Maak de kubus op zijn punt (die lijkt op het hierboven getekende model) af.

Zie figuur bij b.

Neem aan dat de middelste vloer de middens van ribben met elkaar verbindt.

Teken die vloer in jouw kubus.

Neem aan dat de bovenste vloer halverwege de middelste vloer en de top van de kubus zit. Er zijn drie opstaande driehoekige zijwanden op gemaakt.

Teken deze vloer in je kubus inclusief de opstaande zijwanden.

Begin met de driehoekige vloer. Daartoe deel je het lijnstuk vanaf het midden $M$ van de middelste vloer naar de top $G$ in twee gelijke delen. Een horizontale lijn door dit punt in diagonaalvlak $A B G H$ snijdt ribbe $G H$ en dat is een hoekpunt van deze vloer. Nu trek je een lijnstuk evenwijdig aan $H F$ tot ribbe $F G$ en vanuit het punt op die ribbe een lijnstuk evenwijdig aan $F C$ tot ribbe $G C$ en tenslotte weer terug naar het punt op ribbe $G H$ . Let op het stippelen.

Werkblad bij opgave

Je hebt in de voorgaande opgave zelf een eenvoudige kubuswoning getekend. Ga er weer van uit dat de middelste verdiepingsvloer de middens van ribben verbindt en dat de bovenste verdiepingsvloer halverwege de middelste verdiepingsvloer en de top van de kubus zit. Neem aan dat de hoogte tussen de bovenste twee verdiepingsvloeren $2,50$ m is.

Hoe hoog zit dan de top van de kubus boven de onderste punt ervan?

De hoogte tussen deze twee verdiepingen is eenvierde deel van de totale hoogte van de kubus. Die is dus $10$ m.

Hoe groot zijn dan alle ribben van de kubus?

Als die ribben een lengte van $a$ m hebben, dan is $A G = a \sqrt{3} = 10$ . Dus de ribbelengte is $a = \frac{10}{\sqrt{3}} \approx 5,77$ m.

De hoek tussen de lijnstukken $A H$ en $A G$ is de hoek die alle grensvlakken van de kubus met de verticale lijn $A G$ maken. Bereken deze hoek in tienden van graden nauwkeurig.

Omdat $A B G H$ een rechthoekig diagonaalvlak van de kubus is, is $sin(/_ HAG) ~~ (5,77)/10$ , zodat $/_ HAG ~~ 35,3^@$ .

Je ziet hier een balk $A B C D . E F G H$ met daarin de punten $P$ , $Q$ en $R$ die alle drie het midden van een ribbe van de balk vormen.

Zijn de lijnen $ER$ en $FG$ snijdende lijnen?

Ja, ze liggen beide in één vlak, namelijk het bovenvlak en zijn niet evenwijdig.

Zijn de lijnen $ER$ en $PQ$ snijdende lijnen?

Nee, ze liggen niet in één vlak en zijn niet evenwijdig.

Is $ACRE$ een doorsnede van deze balk met een plat vlak?

Nee, want de lijnen $ER$ en $AC$ zijn kruisende lijnen.

Is $EBQR$ een doorsnede van deze balk met een plat vlak?

Ja, want de lijnen $ER$ en $BQ$ snijden elkaar op het verlengde van $FG$ .

Ja, want de lijnen $ER$ en $BQ$ snijden elkaar op het verlengde van $FG$ .
En twee snijdende lijnen vormen precies één vlak.

In kubus $ABCD.EFGH$ is $M$ het midden van $FG$ en $N$ het midden van $GH$ . De ribben van de kubus zijn $6$ cm lang.

Waarom is $DBMN$ de doorsnede van een vlak met deze kubus?

$DB // // NM$ .

Teken deze doorsnede op ware grootte en bereken de hoeken ervan.

De hoeken van $DBMN$ zijn dus $72^@$ , $72^@$ , $108^@$ en $108^@$ .

$DBMN$ is een symmetrisch trapezium met $DB = sqrt(72) ~~ 8,49$ , $MN = sqrt(18) ~~ 4,24$ en $BM = DN = sqrt(45) ~~ 6,71$ . Voor de tekening is ook de hoogte handig. Die is $sqrt((sqrt(45))^2 - (1/2*(sqrt(72)-sqrt(18)))^2) ~~ 6,36$ .

Omdat $sin(/_ BDN) ~~ (6,36)/(6,71)$ is $/_ BDN ~~ 71,6^@$ .
De hoeken van $DBMN$ zijn dus $72^@$ , $72^@$ , $108^@$ en $108^@$ .

Bereken de standhoek van vlak $DBMN$ en het grondvlak $ABCD$ .

$~~ 71^@$

$S$ is het snijpunt van $AC$ en $BD$ .
$T$ is het snijpunt van $EG$ en $MN$ .
De gevraagde standhoek is $/_ CST$ .
$tan(/_ CST) = 6/(1/4*sqrt(72))$ dus $/_ CST ~~ 71^@$ .