de oppervlakte en de inhoud van de ruimtelijke basisfiguren berekenen;

werken met lengte-, oppervlakte- en volumevergrotingsfactoren.

de verschillende ruimtelijke basisfiguren;

gelijkvormigheid, de stelling van Pythagoras en goniometrie toepassen in ruimtelijke figuren;

aanzichten en doorsneden gebruiken bij berekeningen in ruimtelijke figuren.

In deze tabel zie je een aantal bekende formules voor het berekenen van een omtrek, een oppervlakte, of een inhoud. Ernaast staan de betekenissen van die formules, maar die staan niet in de juiste volgorde.

Formule		Betekenis
1	$0,5 xx$ basis $xx$ hoogte	a	omtrek cirkel
2	lengte $xx$ breedte $xx$ hoogte	b	oppervlakte rechthoek
3	grondvlak $xx$ hoogte	c	oppervlakte driehoek
4	$pi xx$ diameter	d	oppervlakte parallellogram
5	lengte $xx$ breedte	e	oppervlakte cirkel
6	$1/3 xx$ grondvlak $xx$ hoogte	f	inhoud balk
7	basis $xx$ hoogte	g	inhoud prisma
8	$pi xx$ straal2	h	inhoud piramide

Geef bij elke formule de juiste omschrijving.

Zie de tabel hieronder.

Formule		Betekenis
1	$0,5 xx$ basis $xx$ hoogte	c	oppervlakte driehoek
2	lengte $xx$ breedte $xx$ hoogte	f	inhoud balk
3	grondvlak $xx$ hoogte	g	inhoud prisma
4	$pi xx$ diameter	a	omtrek cirkel
5	lengte $xx$ breedte	b	oppervlakte rechthoek
6	$1/3 xx$ grondvlak $xx$ hoogte	h	inhoud piramide
7	basis $xx$ hoogte	d	oppervlakte parallellogram
8	$pi xx$ straal2	e	oppervlakte cirkel

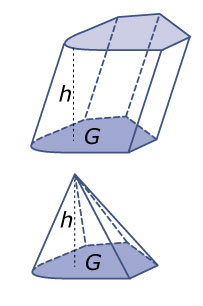
Je ziet hier drie lichamen die alle drie dezelfde hoogte $D H$ hebben. Het prisma en de piramide hebben ook nog hetzelfde grondvlak $A C D$ en dat is precies de helft van het grondvlak van de balk.

De inhoud van de balk is duidelijk het grootst: $V (balk) = 4 \cdot 3 \cdot 6 = 12 \cdot 6 = 72$ eenheden (eenheidskubussen).
Het prisma is de helft van de balk, dus: $V (prisma) = \frac{1}{2} \cdot 4 \cdot 3 \cdot 6 = 6 \cdot 6 = 36$ .
Dit is precies de oppervlakte van het grondvlak ( $Δ A C D$ ) maal de hoogte. Het volume van een prisma is $V (prisma) = G \cdot h$ als $G$ de oppervlakte van het grondvlak en $h$ de hoogte is.

De piramide heeft hetzelfde grondvlak en dezelfde hoogte als het prisma. Je kunt laten zien, dat er in het prisma drie van deze piramides passen. De inhoud van de piramide is daarom $\frac{1}{3}$ deel van die van het prisma. Voor de getekende piramide geldt $V (piramide) = \frac{1}{3} \cdot G \cdot h$ .

Van alle drie de getekende lichamen is de totale oppervlakte gelijk aan de oppervlakte van hun uitslag. En wat gebeurt er met de oppervlakte en de inhoud van zo'n lichaam als alle ribben bijvoorbeeld $3$ keer zo groot worden?

Bekijk de drie lichamen in de Uitleg. De inhoud, het volume, van een lichaam is het aantal eenheidskubusjes dat er in past. Bij een balk en een prisma bepaal je dan eerst het aantal eenheidskubussen op het grondvlak en dan vermenigvuldig je met het aantal lagen, de hoogte, van de balk, het prisma. Zo krijg je de formule $V = G \cdot h$ , waarin $V$ het volume, $G$ de oppervlakte van het grondvlak en $h$ de hoogte is.

Laat zien, dat de formule $V = G \cdot h$ zowel bij de balk als bij het prisma tot de juiste inhoud leidt.

Balk: $G = 4 \cdot 3 = 12$ en $h = 6$ geeft $V = 12 \cdot 6 = 72$ .

Prisma: $G = \frac{1}{2} \cdot 4 \cdot 3 = 6$ en $h = 6$ geeft $V = 6 \cdot 6 = 36$ .

De oppervlakte van een lichaam is de oppervlakte van de uitslag van dat lichaam.

Bereken de oppervlakte van de balk.

$2 \cdot 4 \cdot 3 + 2 \cdot 4 \cdot 6 + 2 \cdot 3 \cdot 6 = 108$ .

Bereken de oppervlakte van het prisma.

Bereken eerst $A C = \sqrt{4^{2} + 3^{2}} = 5$ .
De oppervlakte is dan $2 \cdot \frac{1}{2} \cdot 4 \cdot 3 + 4 \cdot 6 + 3 \cdot 6 + 5 \cdot 6 = 84$ .

Neem nu eens aan dat de afmetingen van deze figuren $3$ keer zo groot worden. Hoeveel keer zo groot wordt dan hun inhoud? En hun oppervlakte? Licht je antwoord toe.

Alle delen van de uitslag worden zowel in de lengterichting als in de breedterichting $3$ keer zo groot. De oppervlakte ontstaat door lengte en breedte te vermenigvuldigen, dus die wordt dan $3 \cdot 3 = 9$ keer zo groot.

En voor de inhoud wordt (net als de lengte en de breedte) ook de hoogte $3$ keer zo groot. De inhoud wordt daarom $3 \cdot 3 \cdot 3 = 27$ keer zo groot.

Bekijk de drie lichamen in de Uitleg. Vergelijk de getekende piramide met het getekende prisma.

Ga na, dat het prisma kan worden verdeeld in de piramides $A C D . H$ , $C G H . E$ en $A H E . C$ .

Doen.

Ga ook na, dat voor elk van deze piramides geldt dat $G \cdot h = 36$ waarin $G$ de oppervlakte van het grondvlak en $h$ de hoogte is.

Van piramide $A C D . H$ is $G = \frac{1}{2} \cdot A D \cdot D C = \frac{1}{2} \cdot 4 \cdot 3 = 6$ en $h = 6$ . Dus $G \cdot h = 36$ .

Van piramide $C G H . E$ is $G = \frac{1}{2} \cdot H G \cdot C G = \frac{1}{2} \cdot 4 \cdot 6 = 12$ en $h = 3$ . Dus $G \cdot h = 36$ .

Van piramide $A H E . C$ is $G = \frac{1}{2} \cdot E H \cdot A E = \frac{1}{2} \cdot 3 \cdot 6 = 9$ en $h = 4$ . Dus $G \cdot h = 36$ .

Leg uit dat de oppervlakte van piramide $A C D . H$ daarom $V = \frac{1}{3} \cdot G \cdot h$ moet zijn. Bereken deze inhoud.

In het prisma met hetzelfde grondvlak als deze piramide en dezelfde hoogte passen drie piramides die dezelfde inhoud als piramide $V = \frac{1}{3} \cdot G \cdot h$ hebben. Van elk van hen is de inhoud dus $V = \frac{1}{3} \cdot G \cdot h$ . En dus is $V (A C D . H) = \frac{1}{3} \cdot 6 \cdot 6 = 12$ .

Er zijn ook lichamen met gebogen grensvlakken. Een cilinder en een kegel bijvoorbeeld hebben ook een grondvlak met oppervlakte $G$ en een hoogte $h$ .

Waarom zal de formule voor de inhoud van een cilinder $V (cilinder) = G \cdot h$ zijn?

Omdat een cilinder lijkt op een prisma. Elke doorsnede loodrecht op de as is hetzelfde. Dus ook bij een cilinder krijg je het volume door het aantal eenheidskubussen op het grondvlak te vermenigvuldigen met het aantal lagen, de hoogte van de cilinder.

Bereken de inhoud van een cilinder met een diameter van $4$ cm en een hoogte van $5$ cm.

$G = pi * 2^2 = 4pi$ en $h = 5$ geeft $V = 4pi*5 = 20pi ~~ 62,8$ cm3.

Waarom zal de formule voor de inhoud van een kegel $V (kegel) = \frac{1}{3} \cdot G \cdot h$ zijn?

Omdat een kegel lijkt op een piramide. Een piramide waarvan het grondvlak een veelhoek is met oneindig veel hoekpunten.

Bereken de inhoud van een kegel met een diameter van $4$ cm en een hoogte van $5$ cm.

$G = pi * 2^2 = 4pi$ en $h = 5$ geeft $V = 1/3 *4pi*5 = 20/3 pi ~~ 20,9$ cm3.

Onder de inhoud of het volume van een lichaam wordt het totaal aantal eenheidskubussen dat dit lichaam opvult verstaan.
Voor verschillende soorten lichamen kun je die inhoud berekenen met behulp van een formule.

De inhoud van een balk, een prisma, of een cilinder met $G$ als oppervlakte van het grondvlak en $h$ als hoogte is: $V = G \cdot h$ .

De inhoud van een piramide, of een kegel met $G$ als oppervlakte van het grondvlak en $h$ als hoogte is: $V = \frac{1}{3} \cdot G \cdot h$ .

Onder de oppervlakte van een lichaam wordt de oppervlakte van de uitslag van dat lichaam verstaan.

Om zowel de inhoud als de oppervlakte van een lichaam te kunnen berekenen moet je de oppervlakteformules van allerlei vlakke figuren, zoals rechthoek, driehoek en cirkel kennen. Ook de formule voor de omtrek van een cirkel is van belang. Zorg dat je al deze formules goed kent!

Als je de afmetingen van een lichaam $k$ keer zo groot maakt, dan wordt de oppervlakte $k^{2}$ keer zo groot en de inhoud $k^{3}$ keer zo groot. $k$ heet de lengtevergrotingsfactor, $k^{2}$ de oppervlaktevergrotingsfactor en $k^{3}$ de volumevergrotingsfactor.

Een cilinder heeft een diameter van $8$ cm en een hoogte van $10$ cm. Bereken de inhoud en de oppervlakte van deze cilinder.

Voor de inhoud $V$ gebruik je de formule $V = G \cdot h$ , waarin $G$ de oppervlakte van het grondvlak en $h$ de hoogte is.

Nu is $G = pi*r^2 = pi*4^2 = 16pi$ en $h = 10$ .
En dus is $V = 16pi*10 = 160pi ~~ 503$ cm3.

Voor de oppervlakte $A$ moet je weten hoe de uitslag van een cilinder er uit ziet. Die bestaat uit twee cirkels en een rechthoek. De rechthoek heeft breedte $10$ cm en als lengte de omtrek van de grondcirkel $pi*8 = 8pi$ cm.
Dus krijg je $A = 8pi * 10 + 2*pi*4^2 = 112pi ~~ 352$ cm2.

In Voorbeeld worden de inhoud en de oppervlakte van een cilinder met gegeven diameter en straal berekend. Neem nu een cilinder met diameter en hoogte precies $2$ keer zo groot.

Laat zien dat de inhoud van deze cilinder $2^{3} = 8$ keer zo groot is als die van de cilinder in het voorbeeld.

De inhoud van de cilinder wordt $V = pi*8^2*20 = 1280pi ~~ 4021$ cm3.
En inderdaad is $1280pi = 8*160pi$ .

Leg uit hoe de oppervlakte van de cilinder in het voorbeeld wordt berekend.

Een uitslag van een cilinder bestaat uit twee cirkels, de grondcirkel en de bovencirkel, met daartussen een rechthoek.
Die rechthoek heeft als lengte de omtrek van zo'n cirkel en als breedte de hoogte van de cilinder.
Met de omtrekformule voor de cirkel reken je de lengte van die rechthoek uit. De oppervlakte is lengte $xx$ breedte.
De oppervlakte van grondcirkel en bovencirkel bereken je met de oppervlakte formule van een cirkel.
Tenslotte tel je de oppervlakte van de rechthoek en de twee cirkels bij elkaar op.

Laat zien dat de oppervlakte van de cilinder in deze opgave $2^{2} = 4$ keer zo groot is als die van de cilinder in het voorbeeld.

De oppervlakte van de cilinder wordt $A = pi*16 * 20 + 2*pi*8^2 = 448pi ~~ 1407$ cm2.
En inderdaad is $448pi = 4*112pi$ .

Een cilindervormig groentenblik heeft een straal van $6$ cm en een hoogte van $16$ cm. Het blik is gemaakt van metaal met een dikte van $1$ mm. De straal en de hoogte zijn gemeten aan de binnenkant van het blik. Je wilt de hoeveelheid metaal die voor dit blik nodig is berekenen als er een plastic deksel op zit.

Je kunt dit op twee manieren doen: de oppervlakte van het blik berekenen en die met de dikte vermenigvuldigen, of van de inhoud van een blik met een straal van $6,1$ cm en een hoogte van $16,1$ cm de inhoud van een blik met straal $6$ cm en hoogte $16$ cm aftrekken.

Voer beide berekeningen uit en geef je antwoord in mm3 nauwkeurig. Waardoor ontstaat het verschil tussen beide antwoorden?

Eerste manier: de oppervlakte is $A = pi*12*16 + pi*6^2 = 228 pi$ , dus de hoeveelheid metaal is $H = 0,1*228 pi = 22,8 pi ~~ 71,628$ cm3.

Tweede manier: de hoeveelheid metaal is $H = pi*6,1^2 * 16,1 - pi*6^2 * 16 = 23,081 pi ~~ 72,511$ cm3.

In feite is de eerste manier onnauwkeurig, omdat er geen rekening is gehouden met de iets bredere grondcirkel (de straal is eigenlijk $6,1$ cm) en met de hoeveelheid metaal die nodig is om van de rechthoek een ronde buis te maken.

Van een cilindervormig literblik zijn hoogte en diameter gelijk.

Bereken de hoogte van de cilinder in mm nauwkeurig.

Noem de straal van de cilinder $r$ en de hoogte $h$ , beide in cm.
Er geldt $h = 2 r$ .
Voor een literblik geldt $V = G*h = pi*r^2*h = 1000$ .

Dus $pi*r^2*2r = 1000$ ofwel $r^3 = 1000/(2pi)$ en $r = (1000/(2pi))^(1/3) ~~ 5,4$ cm.
De hoogte is ongeveer $10,8$ cm.

Deze kartonnen doos heeft de vorm van een vijfzijdig prisma. De voorkant en de achterkant zijn symmetrische vijfhoeken met twee rechte hoeken. De afmetingen vind je bij de figuur.

Bereken de inhoud en de oppervlakte van deze doos.

Voor de inhoud $V$ van deze doos gebruik je de formule $V = G \cdot h$ , waarin $G$ de oppervlakte van het grondvlak en $h$ de hoogte is. Hier is het grondvlak het voorvlak van het prisma, de hoogte is $9$ dm.

Ga na, dat $G = 6 \cdot 6 + \frac{1}{2} \cdot 6 \cdot \sqrt{7} = 36 + 3 \sqrt{7}$ . Nu kun je met de formule berekenen dat de inhoud van de doos ongeveer $395$ dm3 is.

De oppervlakte van de doos is de oppervlakte van de uitslag van deze doos. Die uitslag bestaat uit twee gelijke vijfhoeken (waarvan je de oppervlakte al hebt berekend) en vijf rechthoeken. De totale oppervlakte is de som van de oppervlaktes van deze vijfhoeken en de vijf rechthoeken.

In Voorbeeld zie je hoe je de inhoud en de oppervlakte van een prisma kunt berekenen.

Leg uit hoe de oppervlakte van de vijfhoek die als grondvlak dient, kan worden berekend.

Eerst verdeel je de vijfhoek in een vierkant en twee rechthoekige driehoeken. Het vierkant heeft zijden van $6$ dm en dus is daarvan de oppervlakte $6^{2} = 36$ dm2. De twee rechthoekige driehoeken hebben rechthoekszijden van $3$ dm en $\sqrt{4^{2} - 3^{2}} = \sqrt{7}$ dm. Samen vormen ze een driehoek met een basis van $6$ dm en een hoogte van $\sqrt{7}$ dm en dus een oppervlakte van $\frac{1}{2} \cdot 6 \cdot \sqrt{7}$ .

Reken nu de gevonden inhoud van de doos zelf na.

Doen, gebruik de formule in het voorbeeld.

Bereken de totale oppervlakte van de doos.

$A = 2 * (6^2 + 0,5 * 6 * sqrt(7)) + 3 * 6 * 9 + 2 * 4 * 9 = 306 + 6sqrt(7) ~~ 322$ dm2.

Van een regelmatige vierzijdige piramide $A B C D . T$ is $A B = 4$ cm en $A T = 6$ cm.

Bereken de inhoud en de oppervlakte van deze piramide.

Bereken eerst de hoogte van deze piramide: $h = \sqrt{6^{2} - {(2 \sqrt{2})}^{2}} = \sqrt{28}$ .

De inhoud is dan $V = \frac{1}{3} \cdot 4 \cdot 4 \cdot \sqrt{28} = \frac{16}{3} \sqrt{28}$ cm3.

Bereken vervolgens de hoogtes van de vier gelijke opstaande grensvlakken: $h = \sqrt{6^{2} - 2^{2}} = \sqrt{32}$ .

De totale oppervlakte is dan $A = 4 \cdot 4 + 4 \cdot \frac{1}{2} \cdot 4 \cdot \sqrt{28} = 16 + 8 \sqrt{28}$ cm2.

Bron: Vlaams Instituut voor de Zee

Bij zandwinning ontstaan grote hopen van verschillende soorten zand. Die hopen zand hebben allemaal dezelfde kegelvorm.

Hoeveel m3 zand bevat zo'n kegelvormige hoop met een diameter van $4$ m en een hoogte van $1,50$ m? En hoeveel m3 zand bevat een hoop zand waarvan de afmetingen $2$ keer zo groot zijn?

Voor de inhoud $V$ van een kegel gebruik je de formule $V = \frac{1}{3} \cdot G \cdot h$ , waarin $G$ de oppervlakte van het grondvlak en $h$ de hoogte is. Hier is het grondvlak een cirkel met een straal van $2$ m en de hoogte is $1,50$ m.

De inhoud is dus $V = 1/3 * pi*2^2 * 1,5 = 2pi ~~ 6,28$ m3.

Van de hoop zand waarvan alle afmetingen twee keer zo groot zijn is de lengtevergrotingsfactor $2$ en dus de volumevergrotingsfactor $2^{3} = 8$ . De inhoud van die zandhoop is daarom $2pi*8 = 16pi ~~ 50,27$ m3.

In Voorbeeld zie je hoe je de inhoud van een kegel kunt berekenen.

Bereken de inhoud van een kegel waarvan de straal $5$ cm en de hoogte $10$ cm is.

$V = 1/3 * pi*5^2 * 10 = 250/3 pi ~~ 262$ cm3

Hoeveel bedraagt de inhoud van een kegel waarvan de afmetingen half zo groot zijn als die bij a?

De inhoud wordt dan ${(\frac{1}{2})}^{3} = \frac{1}{8}$ keer zo groot, dus $1/8 * 250/3 pi ~~ 33$ cm3.

Bekijk opnieuw de kegel met straal $5$ en hoogte $10$ cm.
De oppervlakte ervan is gelijk aan de oppervlakte van de uitslag van de kegel.

Laat zien, dat die oppervlakte $A = pi * 5 * sqrt(5^2+10^2)$ is.

De uitslag van de kegel is een cirkelsector met een straal van $sqrt(5^2+10^2)=sqrt(125)$ .
Van deze cirkel met straal $sqrt(125)$ en dus omtrek $2pi*sqrt(125)$ heb je een sector nodig met een cirkelboog van lengte $pi*10$ (de omtrek van de grondcirkel). Dat is het $(pi*10)/(2pi*sqrt(125))$ -de deel.
De oppervlakte daarvan is $(pi*10)/(2pi*sqrt(125))*pi*(sqrt(125))^2 = 5*pi*sqrt(125) = pi*5*sqrt(5^2+10^2)$ .
Je hebt nu de oppervlakte van de grondcirkel niet meegeteld!

Welke formule geldt voor de oppervlakte van een kegel met straal $r$ en hoogte $h$ als je het grondvlak niet meerekent?
En als je het grondvlak wel meerekent?

Zonder grondvlak: $A = pi * r * sqrt(r^2+h^2)$

Met grondvlak: $A = pi * r * sqrt(r^2+h^2) + pi*r^2$

In een betonblok in de vorm van een kubus met ribben van $50$ cm wordt een kegelvormig gat geboord. Dit kegelvormige gat heeft een diameter van $15$ cm en een diepte van $40$ cm.

Uit hoeveel cm3 beton bestaat dit betonblok met gat?
Het blok met gat wordt geverfd. Hoeveel cm2 bedraagt de oppervlakte?

Voor het betonblok zonder gat is $50 \cdot 50 \cdot 50 = 125000$ cm3 beton nodig. Het gat heeft een volume van $1/3 * pi * 7,5^2 * 40 ~~ 2356$ cm3.
Voor het betonblok met gat is $122644$ cm3 beton nodig.

De oppervlakte is gelijk aan de oppervlakte van de kubus minus een cirkel met straal $7,5$ en plus een kegeloppervlak.
Dus $A = 6*50*50 - pi*7,5^2 + pi*7,5*sqrt(7,5^2 + 40^2) ~~ 15782$ cm2.

Verfblikken zijn er in allerlei maten. In deze opgave wordt uitgegaan van een wiskundig model van een verfblik: een cilinder met een cirkel als bodem en een cirkel als deksel. Houd geen rekening met de dikte van het blik.

Een verfblik heeft een hoogte van $14$ cm en een straal van $8$ cm.

Bereken hoeveel cm3 de inhoud van het verfblik is. Rond je antwoord af op een geheel getal.

$V = pi * 8^2 * 14 ~~ 2815$ cm3.

Teken op schaal $1 : 4$ de uitslag van dit verfblik. Schrijf op hoe je de maten van je tekening gevonden hebt.

Op ware grootte krijg je een rechthoek van $2 pi * 8 = 16pi$ bij $14$ met daarbij twee cirkels met straal $8$ cm.
Op schaal $1 : 4$ wordt dit een rechthoek van $4pi ~~ 12,6$ bij $3,5$ cm met twee cirkels met een straal van $2$ cm.

Als je de straal van een blik verdubbelt en de hoogte halveert, blijft de inhoud van het blik dan hetzelfde? Laat zien hoe je het antwoord hebt gevonden.

De inhoud wordt $V = pi * 16^2 * 7 ~~ 5630$ cm3.
Dus $2$ keer zo groot.

Een spaarpot heeft de vorm van een regelmatige piramide met een vierkant grondvlak. In de linkerfiguur hieronder zie je een tekening van de spaarpot. Daarnaast staat een wiskundig model met de maten van de spaarpot.

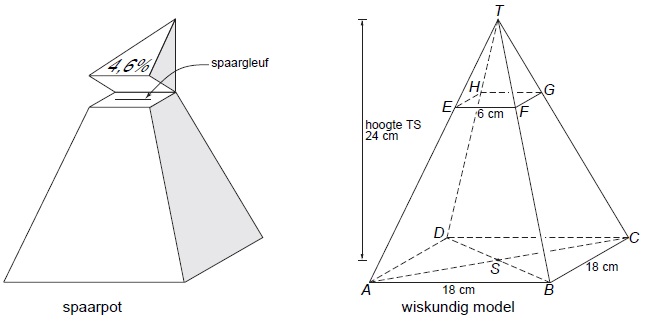
De spaarpot heeft een deksel. Dat is piramide $T . E F G H$ . Het scharnier, waarom de deksel omgeklapt kan worden, is lijnstuk $H G$ .

De bank die deze spaarpot cadeau geeft beweert dat de inhoud van de deksel $4,6$ % van de inhoud van de hele piramide is. Laat met een berekening zien dat dit niet waar is.

De afmetingen van het deksel zijn $\frac{1}{3}$ deel van die van de hele spaarpot.
De volumevergrotingsfactor is daarom ${(\frac{1}{3})}^{3} = \frac{1}{27}$ , dus het volume van de deksel is $\frac{1}{27}$ deel van dat van de gehele piramide en dat is $\frac{1}{27} \approx 0,037$ deel, dus $3,7$ %.

De spaarpot wordt cadeau gegeven in de vorm van een bouwplaat. Hoeveel oppervlakte aan karton is er nodig voor deze spaarpot? Houd geen rekening met de opening om geld in te doen en geef je antwoord in cm2 nauwkeurig.

De spaarpot bestaat uit een grondvlak van $18$ cm bij $18$ cm, vier opstaande driehoekige zijvlakken met een basis van $18$ cm en een hoogte van $\sqrt{24^{2} + 9^{2}} = \sqrt{657}$ cm en twee scheidingsvlakjes van $6$ bij $6$ cm.

De benodigde hoeveelheid karton is daarom $4 \cdot \frac{1}{2} \cdot 18 \cdot \sqrt{657} + 18^{2} + 2 \cdot 6^{2} \approx 1319$ cm2 karton (exclusief plakrandjes).

Op de foto hiernaast zie je een houder waarin een sfeerlichtje zit. Deze sfeerlichthouder heeft de vorm van een prisma met een gelijkzijdige driehoek als grondvlak. Op de foto hieronder zie je het bovenaanzicht van een figuur gemaakt van zes van deze sfeerlichthouders.

Geef de kleinste hoek in graden waarover dit bovenaanzicht draaisymmetrisch is.

Omdat het hier zes gelijkzijdige driehoeken betreft die hoeken van $60^@$ hebben, is de kleinste draaihoek ook $60^@$ .

Hieronder zie je een tekening van de sfeerlichthouder. De sfeerlichthouder is massief en gemaakt van kunststof. De zijden van het driehoekige grondvlak zijn $10$ cm. De hoogte van de sfeerlichthouder is $2$ cm. Precies in het midden van de sfeerlichthouder zit een rond gat voor het sfeerlichtje. De diameter van dit gat is $3,8$ cm en de diepte is $1,2$ cm.

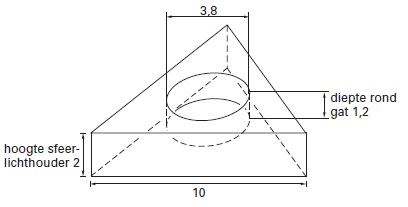
Bereken in hele cm3 hoeveel kunststof er nodig is om deze sfeerlichthouder te maken.

Het gaat om de inhoud van een regelmatig driezijdig prisma met als grondvlak een gelijkzijdige driehoek met een basis van $10$ cm en een hoogte van $\sqrt{10^{2} - 5^{2}} = \sqrt{75}$ cm en een eigen hoogte van $2$ cm. Daarvan moet de inhoud van een cilinder met een straal van $1,9$ cm en een hoogte van $1,2$ cm worden afgetrokken.

Er is dus $1/2 * 10 * sqrt(75) * 2 - pi * 1,9^2 * 1,2 ~~ 73$ cm3 kunststof voor nodig.

Droste chocolaatjes worden onder andere verpakt in kartonnen doosjes zoals je die hiernaast ziet. De bodem van deze doosjes is een regelmatige achthoek met zijden van ongeveer $7,8$ cm. De hoogte van zo'n Drostedoosje is ongeveer $3,3$ cm. Nadat je alle chocolaatjes op hebt haal je het plastic waar ze in hebben gelegen uit het doosje.

Bereken de inhoud van het doosje in cm3 nauwkeurig.

Het grondvlak bestaat uit acht gelijkbenige driehoeken met een basis van $7,8$ cm en een tophoek van $(360^@)/8 = 45^@$ .
Voor de hoogte $h$ van zo'n driehoek geldt: $tan(22,5^@) = (3,9)/h$ en dus $h = (7,9)/(tan(22,5^@)) ~~ 9,42$ .
De oppervlakte van het grondvlak is daarmee ongeveer $8 \cdot \frac{1}{2} \cdot 7,8 \cdot 9,42 \approx 293,8$ cm2.

Het volume is ongeveer $293,8 \cdot 3,3 \approx 969,4$ cm3.

Een model van dit Drostedoosje is een regelmatig achthoekig prisma met opstaande ribben van $3,3$ cm en andere ribben van $7,8$ cm. Bereken de oppervlakte van zo'n prisma in cm2 nauwkeurig.

Van het grondvlak (en dus ook van het bovenvlak) is de oppervlakte al berekend bij a. Alle andere grensvlakken zijn rechthoeken van $7,8$ cm bij $3,3$ cm.

De oppervlakte is dus $2 \cdot 293,8 + 8 \cdot 7,8 \cdot 3,3 \approx 793$ cm2.

Je ziet hier een cilindervormige plastic bak waar een kegel uit is weggesneden.

Bereken de hoeveelheid plastic die hiervoor nodig is.

$pi * 4^2 * 10 - 1/3 * pi * 4^2 * 10 ~~ 335$ cm3.

Bereken de hoeveelheid plastic die nodig is voor eenzelfde bak waarvan alle afmetingen $1,5$ keer zo groot zijn.

$1,5^3 * 335,10... ~~ 1131$ cm3.

De oorspronkelijke plastic bak wordt groen gespoten. Hoeveel cm2 moet de verflaag bedekken?

De kegelmantel is het $(2pi *4)/(2pi sqrt(4^2 + 10^2))$ -de deel van $pi*(sqrt(4^2+10^2))^2$ en heeft dus een oppervlakte van $pi * 4 * sqrt(4^2 + 10^2)$ .

$pi * 4^2 + pi * 8 * 10 + pi * 4 * sqrt(4^2 + 10^2) ~~ 437$ cm2.

Hier zie je een vereenvoudigd model van het dak van een stolpboerderij. Het dak is zuiver symmetrisch, dus de ribben $A E$ , $D E$ , $B F$ en $C F$ zijn even lang en $E F$ loopt evenwijdig met $A B$ en $C D$ . Dit is een samengestelde ruimtelijke figuur, die bestaat uit een prisma en twee piramides die je tot één piramide kunt samenvoegen.

De hoeken van de verschillende delen van zo'n dak kun je berekenen en ook allerlei lengtes die je nodig hebt om ze op schaal te tekenen zijn te berekenen.

Als je op weg naar huis om je heen kijkt onderweg, zul je daken in verschillende vormen tegenkomen. Bijna altijd valt er met de hulpmiddelen die je in dit onderdeel hebt gebruikt aan te rekenen. En dat is nuttig, al is het maar om te kunnen berekenen hoeveel m2 aan dakbedekking ervoor nodig is.

Bekijk het sterk vereenvoudigde dak van een stolpboerderij. Gebruik de gegevens in de figuur.

Bereken het volume onder dit dak en boven de zoldervloer.

Het volume van het middendeel onder het dak is dat van een prisma met als grondvlak een opstaande driehoek met een hoogte van $5$ m en een basis van $8$ m. De hoogte van het prisma is $6$ m (de nok van het dak).
Het volume van de twee uiteinden van het dak is dat van een piramide met een hoogte van $5$ m en als grondvlak een rechthoek van $6$ m bij $8$ m.

De inhoud is daarom $\frac{1}{2} \cdot 8 \cdot 5 \cdot 6 + \frac{1}{3} \cdot 6 \cdot 8 \cdot 5 = 200$ m3.

Gebruik de gegevens in de figuur van het dak van de stolpboerderij hierboven.

Bereken de oppervlakte van het dak.

Het dak bestaat uit twee driehoeken met een basis van $8$ m en een hoogte van $\sqrt{5^{2} + 3^{2}} = \sqrt{34}$ en twee trapezia met een hoogte van $\sqrt{5^{2} + 4^{2}} = \sqrt{41}$ .

De oppervlakte is daarom $2 \cdot \frac{1}{2} \cdot 8 \cdot \sqrt{34} + 2 \cdot \frac{1}{2} \cdot (12 + 6) \cdot \sqrt{41} = 8 \sqrt{34} + 18 \sqrt{41}$ m2.

Je ziet hier chocoladeverpakking in de vorm van een prisma.
De twee driehoeken aan de voorkant en de achterkant zijn gelijkzijdig en hebben zijden van $4$ cm. De totale lengte van de verpakking is $24$ cm.

Bereken het volume van deze verpakking.

$~~ 166,3$ cm3.

$V = 1/2 * 4 * sqrt(12) * 24 ~~ 166,3$ cm3.

Je wilt weten hoeveel materiaal ervoor nodig is om zo'n verpakking te maken.
Bereken daartoe de totale buitenoppervlakte ervan.

$~~ 302$ cm4.

$A = 2 * 1/2 * 4 * sqrt(12) + 3 * 4 * 24 ~~ 302$ cm2.

Voor reclamedoeleinden wordt zo'n verpakking op veel grotere schaal gemaakt.
Alle afmetingen worden $25$ keer zo groot gemaakt.

Hoe groot worden de inhoud en de oppervlakte van deze grotere verpakking?

Het volume wordt $~~ 2598076$ cm3.

De oppervlakte wordt $~~ 188660$ cm2.

Het volume wordt $~~ 25^3 * 166,3 ~~ 2598076$ cm3.

De oppervlakte wordt $~~ 25^2 * 302 ~~ 188660$ cm2.

Een kegel wordt gevormd uit een halve cirkel met een diameter van $40$ cm.
Hoe groot zijn de oppervlakte en de inhoud van die kegel?

Oppervlakte $~~ 628$ cm2.

Inhoud $~~ 1814$ cm3.

De oppervlakte is $A = 1/2 * pi * 20^2 ~~ 628$ cm2.

Omtrek grondcirkel wordt $20pi$ cm, dus diameter $20$ cm.

Dan is $h = sqrt(20^2-10^2) ~~ 17,3$ cm.

De inhoud is $V = 1/3 * pi * 10^2 * 17,3 ~~ 1814$ cm3.