In dit onderwerp gaat het over meetkundige berekeningen aan ruimtelijke figuren. Daarbij worden gelijkvormigheid, de stelling van Pythagoras, goniometrie, de sinusregel en de cosinusregel toegepast. Ook de oppervlakte en de inhoud van de basisvormen (kubus, balk, prisma, piramide, cilinder en kegel) worden berekend.

Je hebt nu alle theorie van Ruimtelijke figuren doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan... Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je ermee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

lichaamveelvlak, ribbe, hoekpunt zijvlaksdiagonaal, lichaamsdiagonaal, diagonaalvlakgrondvlak, hoogte

parallelprojectiedrieaanzicht, voor-, zij-, bovenaanzicht

doorsnedekruisende lijnen

inhoud, volumeoppervlaktelengte-, oppervlakte-, volumevergrotingsfactor

in ruimtelijke figuren gelijkvormigheid, de stelling van Pythagoras en goniometrie (ook sinusregel en cosinusregel) gebruiken;

aanzichten van ruimtelijke figuren tekenenaanzichten gebruiken bij berekeningen;

kruisende lijnen herkennendoorsneden herkennendoorsneden gebruiken voor berekeningen en ze op ware grootte tekenen;

inhoud en oppervlakte van de basisvormen berekenenoppervlakte- en volumevergroting berekenen bij een gegeven lengtevergrotingsfactor.

Hieronder zie je een boombank die bestaat uit zes gelijke delen waar je op kunt zitten. De regelmatige zeshoek die de buitenrand van deze boombank voorstelt heeft zijden van $120$ cm. De regelmatige zeshoek die de binnenrand van deze boombank voorstelt heeft zijden van $80$ cm.

Hoeveel bedraagt de oppervlakte van deze boombank? Geef je antwoord in cm2 nauwkeurig.

Een regelmatige zeshoek bestaat uit zes gelijkzijdige driehoeken. Als de zijden van die zeshoek $120$ cm zijn is van elk van die driehoeken de basis $120$ cm en de hoogte $60 \sqrt{3}$ cm. De oppervlakte van zo'n zeshoek is dan $6 \cdot \frac{1}{2} \cdot 120 \cdot 60 \sqrt{3} = 21600 \sqrt{3}$ . Als de zijden van die zeshoek $80$ cm zijn is van elk van die driehoeken de basis $80$ cm en de hoogte $40 \sqrt{3}$ cm. De oppervlakte van zo'n zeshoek is dan $6 \cdot \frac{1}{2} \cdot 80 \cdot 40 \sqrt{3} = 9600 \sqrt{3}$ .

De boombank heeft dus een oppervlakte van $12000 \sqrt{3} \approx 20785$ cm2.

Hieronder zie je twee foto’s van een ijsje. Het model van het ijsje past precies in een balk $A B C D . E F G H$ , waarvan de vlakken $A B C D$ en $E F G H$ vierkant zijn. Het model bestaat uit vier even grote, gelijkbenige driehoeken. In deze driehoeken geldt $A F = A H = C F = C H = 9,8$ cm en $A C = F H = 6$ cm. Voor het maken van de verpakking wordt eerst een uitslag getekend en daarna de oppervlakte uitgerekend.

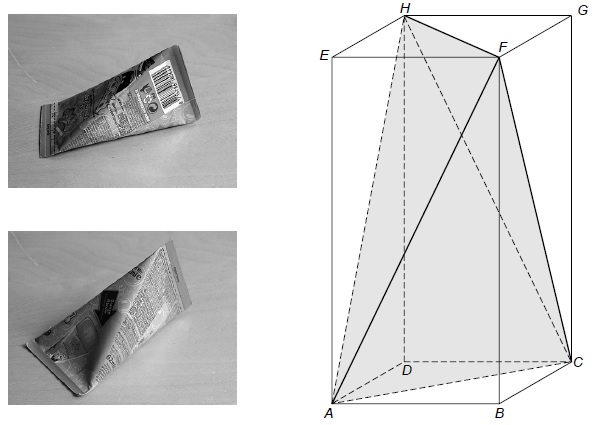
Maak zelf zo'n uitslag en zet de hoekpunten op de juiste plek.

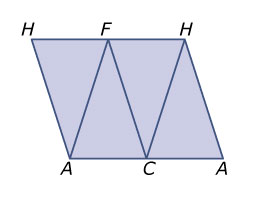
De uitslag bestaat uit vier gelijkbenige driehoeken met benen van $9,8$ cm en een basis van $6$ cm.

Bereken de oppervlakte van deze uitslag in cm2 nauwkeurig.

Elk van de vier gelijkbenige driehoeken heeft een basis van $6$ cm en een hoogte van $\sqrt{{9,8}^{2} - 3^{2}} \approx 9,33$ cm. De oppervlakte van de uitslag is dus $4 \cdot \frac{1}{2} \cdot 6 \cdot 9,33 \approx 112$ cm2.

Bereken de grootte van $/_ AFC$ in graden nauwkeurig.

$sin(1/2 /_ AFC) = 3/(9,8)$ dus $/_ AFC ~~ 36^@$ .

Een groot blik verf heeft een diameter van $24$ cm en een hoogte van $30$ cm. De gebogen zijkant van het blik is geheel bedekt met papier. Daarop staat (behalve de noodzakelijke informatie) de naam van de fabrikant met letters van wel $12$ cm hoog.

Hoeveel liter verf past er in zo'n blik?

$pi*12^2*30 ~~ 13571$ cm3 en dat is ongeveer $13,6$ liter.

Hoeveel cm2 papier gaat er om dit blik?

$pi*24*30 ~~ 2262$ cm2 papier.

Er zijn ook blikken waarvan alle afmetingen maar half zo groot zijn.
Hoe groot is dan het stuk papier dat er omheen gaat en hoe groot worden de letters van de naam van de fabrikant als die naar verhouding worden verkleind?

$~~ (1/2)^2 * 2262 ~~ 565$ cm2 papier en de letters worden $6$ cm hoog.

Gegeven is een balk $A B C D . E F G H$ met $A B = B C = 10$ en $A E = 12$ cm. Punt $P$ is het midden van ribbe $E H$ en punt $Q$ is het midden van ribbe $H G$ .

Waarom zijn $A P$ en $C Q$ snijdende lijnen?

Omdat ze beide in de doorsnede $A C Q P$ van een vlak met de balk liggen. Immers $P Q / / A C$ .

Waarom zijn $A P$ en $C G$ kruisende lijnen?

De lijnen $P G$ en $A C$ zijn niet evenwijdig, dus deze punten liggen niet in één vlak.

Bereken de oppervlakte van de doorsnede $A C Q P$ van een vlak met de gegeven balk.

Deze vierhoek is een trapezium met $A C = \sqrt{200}$ , $P Q = \sqrt{50}$ en $A P = C Q = \sqrt{5^{2} + 12^{2}} = 13$ . De hoogte van dit trapezium is $\sqrt{13^{2} - {(0,5 \sqrt{50})}^{2}} = \sqrt{156,5}$ .

De oppervlakte van $A C Q P$ is daarom $\frac{1}{2} \cdot (10 \sqrt{2} + 5 \sqrt{2}) \cdot \sqrt{156,5} \approx 133$ cm2.

Bereken de hoeken van de doorsnede $A C Q P$ .

$sin(/_ CAP) = (sqrt(156,5))/13$ dus $/_ CAP ~~ 74^@$ .
Dus de hoeken zijn ongeveer $74^@$ , $74^@$ , $106^@$ en $106^@$ .

Bekijk de afbeelding met een woonhuis van het Guragevolk in Ethiopië, dat bestaat uit een cilinder en een kegel. Het vooraanzicht van zo'n woonhuis is afgebeeld.

De dakbedekking loopt wat langer door, waardoor de diameter van de dakbedekking $5,2$ meter is.

Bereken de oppervlakte van het woonhuis. Tel de vloer daar niet bij mee.

Geef het antwoord in een geheel aantal m2.

De oppervlakte is $~~ 41$ m2.

De oppervlakte van het huis bestaat uit de oppervlakte van een cilinder zonder grondvlak/bovenvlak en de oppervlakte van een kegel zonder grondvlak.

$text(oppervlakte cilinder zonder grondvlak/bovenvlak) = 2*pi*r*h$

met $r$ de straal van het grondvlak van de cilinder en $h$ de hoogte van de cilinder

$text(oppervlakte cilinder zonder grondvlak/bovenvlak) = 2*pi*2,4*2,2 = 33,2$ m2

$text(oppervlakte kegelmantel) = pi*r*sqrt(r^2 + h^2)$

met $r$ de straal van het grondvlak van de kegel en $h$ de hoogte van de kegel

$h = (2,2 + 2,2) - 2 = 2,4$

$text(oppervlakte kegelmantel) = pi*2,6*sqrt(2,6^2 + 2,4^2) = 28,9$ m2

$text(oppervlakte huis) = 33,2 + 28,9 = 62,1 = 62$ m2

Met betonnen elementen kunnen zandbakken van verschillende vormen worden gemaakt. In de foto hieronder zijn vier elementen aangegeven.

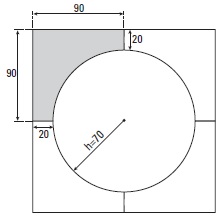
Van zo'n element is hiernaast een bovenaanzicht getekend, met de maten erbij. De hoogte van elk element is $65$ cm.

Hoeveel cm3 beton is er voor elk element nodig?

$90 * 90 * 65 - 1/4 * pi * 70^2 * 65 ~~ 276351$ cm3.

Om de elementen tegen graffiti te beschermen wordt het hele element in de fabriek met een vloeistof behandeld.

Bereken in gehele cm2 nauwkeurig de oppervlakte die per element behandeld moet worden. Schrijf je berekening op.

$2 * 90 * 65 + 2 * 20 * 65 + 1/4 * 2pi * 70 * 65 + 2 * (90 * 90 - 1/4 * pi * 70^2) ~~ 29950$ cm2.

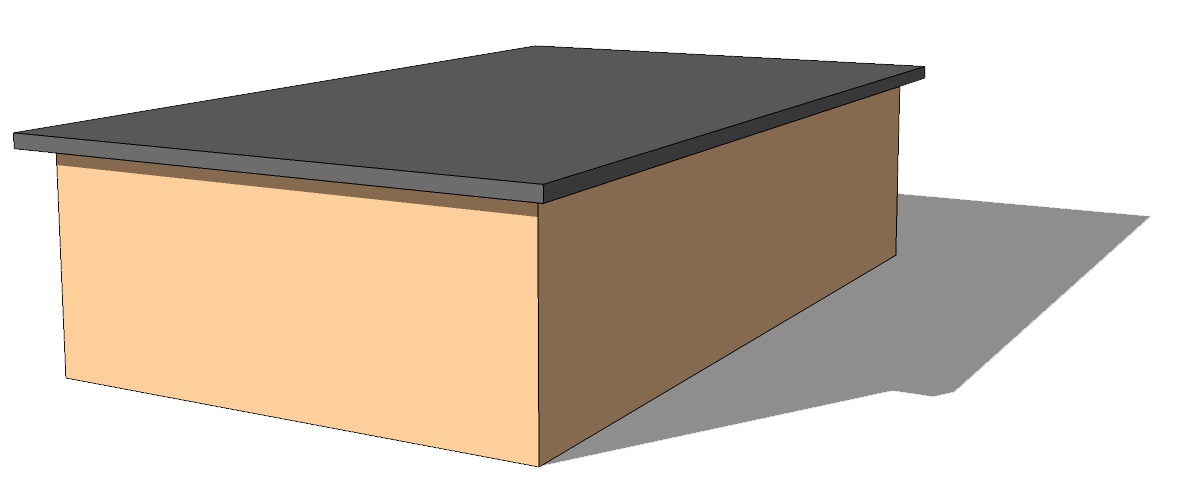
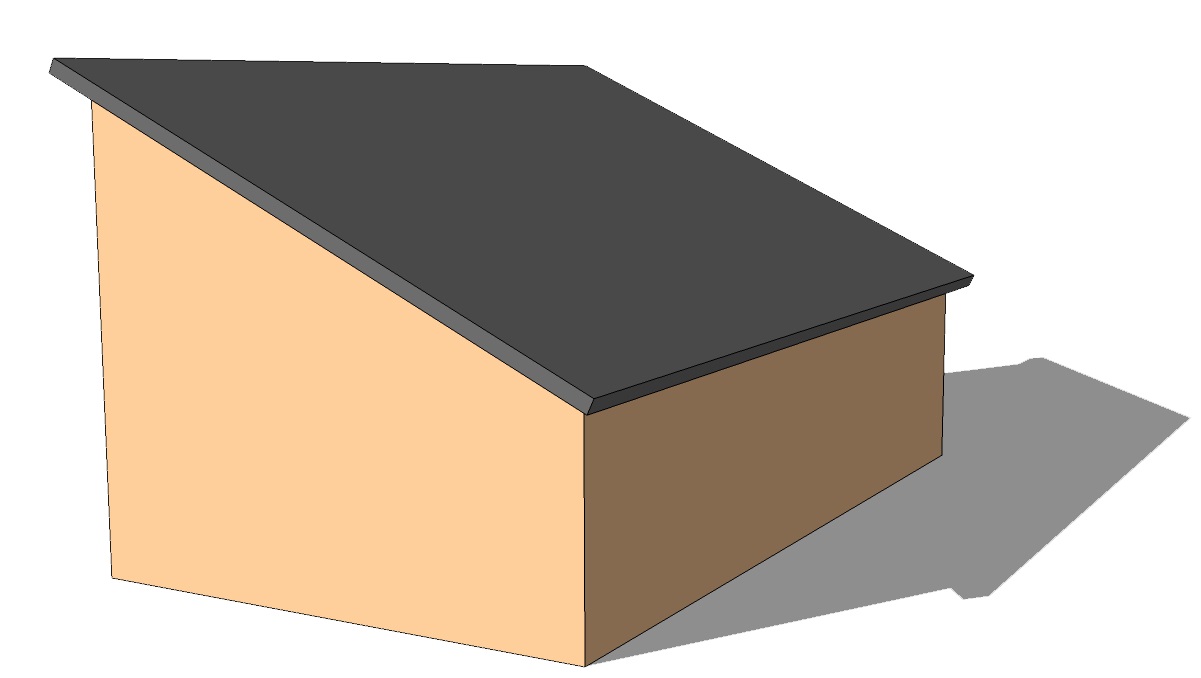
Hier zie je vier tekeningen van huizen met een bepaald soort dak, gemaakt door Michel Stomphorst van Dutch Design Studio.

plat dak

lessenaarsdak

zadeldak

schilddak

De warmte-energie die een gebouw uit kan stralen wordt bepaald door de verhouding

$(A_0)/V$

Hierin is:

$A_0$ de totale oppervlakte van het gebouw in m2

$V$ het volume van het gebouw in m3

Hoe groter de waarde van deze verhouding, hoe meer warmteverlies het gebouw heeft.

Warmte-energie uitstraling

Bekijk eerst de verhouding $(A_0)/V$ voor verschillende balkvormen.

Bereken deze verhouding voor:

een kubus van $8 xx 8 xx 8$ m

een balk van $8 xx 16 xx 4$ m

een balk van $4 xx 32 xx 4$ m

Je krijgt:

voor een kubus van $8 xx 8 xx 8$ m:
$V = 512$ m3, $A_0 = 6*8*8 = 384$ m2, dus $(A_0)/V = 0,75$ .

een balk van $8 xx 16 xx 4$ m:
$V = 512$ m3, $A_0 = 2*8*4+2*8*16+2*4*16 = 448$ m2, dus $(A_0)/V = 0,875$ .

een balk van $4 xx 32 xx 4$ m:
$V = 512$ m3, $A_0 = 2*4*4+4*4*32 = 544$ m2, dus $(A_0)/V = 1,0625$ .

Welke vorm heeft de gunstigste verhouding $(A_0)/V$ ?

De kubus, want die heeft naar verhouding de kleinste oppervlakte bij gelijkblijvend volume.

Neem een kubus met ribbelengte $r$ . Hoe hangt de verhouding $(A_0)/V$ af van $r$ ? En wat betekent dit als $r$ groter wordt?

$V = r^3$ , $A_0 = 6*r^2 = 448$ , dus $(A_0)/V = (6r^2)/(r^3) = 6/r$ .
Als $r$ groter wordt, wordt deze verhouding kleiner.

Van een bol met straal $r$ is de oppervlakte $A_0 = 4pi r^2$ en de inhoud $V = 4/3 pi r^3$ .

Is de verhouding $(A_0)/V$ voor een bol gunstiger dan voor een kubus?

Nu is $(A_0)/V = (4pi r^2)/(4/3 pi r^3) = 3/r$ .
Voor een bol is deze verhouding altijd kleiner dan voor een kubus.

Warmteverlies van huizen

Ga er van uit dat van elk van de huizen de begane grond een rechthoek van $5$ bij $8$ m is en dat de hoogte tot de dakrand $3$ m is.
Verder is de standhoek van het lessenaarsdak met een horizontaal vlak $30^@$ en zijn alle standhoeken van het zadeldak en het schilddak met een horizontaal vlak $60^@$ .

Bereken van elk van de vier huizen de verhouding $(A_0)/V$ .
Welk van deze huizen heeft naar verhouding het minste warmteverlies?

Je krijgt:

huis met plat dak:
$V = 120$ m3, $A_0 = 2*8*5+2*8*3+2*5*3 = 158$ m2, dus $(A_0)/V ~~ 1,32$ .

huis met lessenaarsdak:
$tan(30^@) ~~ 0,577$ geeft voor de extra hoogte links $~~ 5*0,577~~2,89$ m.
De breedte van het dak wordt dan $sqrt(5^2 + 2,89^2)~~5,77$ .
$V ~~ 5*8*3+1/2*5*8*2,89~~177$ m3, $A_0 ~~ 2*5*3+2*1/2*5*2,89+2*8*3+5*8+5,77*8 ~~ 179$ m2, dus $(A_0)/V = 1,00$ .

huis met zadeldak:
$tan(60^@) ~~ 1,732$ geeft voor de extra hoogte midden $~~ 2,5*1,732~~4,33$ m.
De breedte van de dakdelen wordt dan $sqrt(2,5^2 + 4,33^2)=5$ .
$V ~~ 5*8*3+1/2*5*8*4,33~~207$ m3, $A_0 ~~ 2*5*3+2*1/2*5*4,33+2*8*3+5*8+2*5*8 ~~ 180$ m2, dus $(A_0)/V = 0,87$ .

huis met schilddak:
$tan(60^@) ~~ 1,732$ geeft voor de extra hoogte midden $~~ 2,5*1,732~~4,33$ m.
Hoogte voorste/achterste dakdelen wordt $sqrt(2,5^2 + 4,33^2)=5$ .
Linker/rechter dakdelen zijn trapezia met hoogte $sqrt(2,5^2 + 4,33^2)=5$ .
$V ~~ 5*8*3+1/3*5*5*4,33+1/2*3*5*4,33~~189$ m3, $A_0 ~~ 2*5*3+2*8*3+2*1/2*5*5+2*1/2*(8+3)*5 ~~ 158$ m2, dus $(A_0)/V = 0,84$ .

Het huis met het schilddak kent het minste warmteverlies.
Hoewel: de vergelijking met het huis met het zadeldak gaat niet zo goed op omdat dit laatste huis ook groter is. Je zou eigenlijk twee van deze huizen met hetzelfde volume moeten vergelijken!