breuken handmatig optellen, aftrekken, vermenigvuldigen en delen;

rekenen met breuken op de rekenmachine.

het begrip breuk, breuken vereenvoudigen en omrekenen naar een decimaal getal;

breuken vergelijken door gelijknamig maken.

Ton en Hans delen opslagruimte op een harde schijf. Ton neemt de helft van de schijf in beslag, Hans neemt $3/8$ deel.

Welk deel (breuk) van de werkruimte hebben ze samen in gebruik?

$7/8$

Welk deel van de werkruimte heeft Ton meer dan Hans?

$1/8$

Ton heeft van zijn opslagruimte al $3/4$ deel gevuld met data.

Welk deel van de totale werkruimte is dat?

$3/8$

Leg uit dat het bij de vorige opgave eigenlijk ging om het vermenigvuldigen van twee breuken.

$3/4$ van $1/2$ is $3/4 xx 1/2$ .

Gelijknamige breuken kun je eenvoudig bij elkaar optellen of van elkaar aftrekken:

$3/7 + 2/7 = 5/7$

$5/7 - 2/7 = 3/7$

Als breuken niet gelijknamig zijn, moet je ze eerst gelijknamig maken!

$1/2 + 1/3 = 3/6 + 2/6 = 5/6$ .

Denk er wel om dat beide breuken delen van hetzelfde geheel moeten zijn!

Bereken en vereenvoudig daarna zoveel mogelijk:

$5/9 + 1/9$

$6/9 = 2/3$

$11/12 - 7/12$

$4/12 = 1/3$

$3 7/12 + 11/12$

$3 18/12 = 4 1/2$

$4 1/3 - 2 2/3$

$1 2/3$

Je wilt de breuken $1/2$ en $3/8$ optellen.

Beide breuken zijn niet gelijknamig. Ze zijn wel gemakkelijk gelijknamig te maken. Hoe?

$1/2 = 4/8$ .

Hoeveel is dus $1/2 + 3/8$ ?

$4/8 + 3/8 = 7/8$ .

En hoeveel is $1/2 - 3/8$ ?

$4/8 - 3/8 = 1/8$ .

Bekijk Uitleg.

Maak zelf zo'n tekening bij $2/5 + 1/4$ .

Doen, laat eventueel je figuur controleren.

Waarom moeten de twee rechthoeken waarvan je $2/5$ en $1/4$ deel hebt aangegeven even groot zijn?

Anders zijn beide breuken geen deel van hetzelfde en kun je ze dus niet optellen.

Waarom maak je de éne verdeling horizontaal en de andere verticaal?

Dan zie je beter hoe de verdeling van het geheel in $20$ kleinere rechthoekjes tot stand komt.

Bereken $2/5 + 1/4$ .

$8/20 + 5/20 = 13/20$ .

Je kunt $2/5 + 1/4$ ook exact berekenen met de rekenmachine. Je hebt behalve de toetsen voor de cijfers alleen de toetsen en nodig.

Wat is dan de uitkomst van deze optelling?

$2//5 + 1//4$ invoeren geeft $0,65$ .

$3/5$ deel van $35$ kun je als volgt berekenen:

$1/5$ deel van $35$ is $7$ ;

$3/5$ deel is $3$ keer $1/5$ deel, dus $3 xx 7 = 21$ .

En $2/7$ deel van $3/5$ deel is zo $2/7 xx 21 = 6$ . En $6$ is $6/35$ deel van $35$ .

Je ziet dat $2/7$ van $3/5$ hetzelfde is als $6/35$ . Dus: $2/7 xx 3/5 = (2 xx 3)/(7 xx 5) = 6/35$ .

Zo kun je breuken vermenigvuldigen: je vermenigvuldigt de tellers met elkaar en de noemers met elkaar.

Opmerking:
In plaats van $xx$ gebruik je voor vermenigvuldigen meestal $*$ : $2 * 3 = 2 xx 3$ .

Als je een getal deelt door een breuk, kijk je hoe vaak die breuk in dat getal past. Zo kun je de uitkomst van $14 // 1/2$ voorstellen als het antwoord op de vraag: Hoeveel halve euro's passen er in $14$ hele euro's? Je ziet dan dat $14 // 1/2 = 28$ .

Je kunt ook twee breuken op elkaar delen.
Een munt van 0,50 is $1/2$ euro. Een munt van 0,10 is $1/10$ euro.
Stel je wilt weten hoeveel munten van 0,10 er gaan in een munt van 0,50. Dan reken je eigenlijk uit: $1/2 // 1/10$ . De uitkomst is $5$ zoals je wel weet. Dus: $1/2 // 1/10 = 5$ .
Dit komt omdat $1/2 = 5/10$ .

Dus: $1/2 // 1/10 = 5/10 // 1/10 = 5//1 = 5$ .
Je ziet dat het handig is om beide breuken gelijknamig te maken.

Je kunt ook zo redeneren: $1/2 // 1/10 = (1/2)/(1/10) = (1/2*10/1)/(1/10*10/1) = (1/2 * 10/1)/1 = 1/2 * 10/1 = 5$ .
Je hebt dan beide breuken vermenigvuldigd met het omgekeerde van de tweede breuk.

Bekijk de vermenigvuldiging $6/7 xx 5/8$ .

Voer de vermenigvuldiging met de hand uit.

$6/7 xx 5/8 = (6 xx 5)/(7 xx 8) = 30/56$ .

Kun je de breuk nog vereenvoudigen?

Ja, dat kan: $30/56 = 15/28$ .

Je kunt ook vereenvoudigen voordat je de tellers en de noemers vermenigvuldigt. Laat zien hoe dat gaat.

$6/7 xx 5/8 = (6 xx 5)/(7 xx 8) = (3 xx 5)/(7 xx 4) = 15/28$ .

Je hebt nog $2 1/2$ taart. Je geeft iedereen $1/6$ deel van een taart.

Hoeveel personen kun je een stuk taart geven?

$15$

Welke deling van breuken hoort hier bij?

$2 1/2 // 1/6$ .

Maak beide breuken gelijknamig. Leg nu uit hoe je het antwoord op a kunt zien aan beide breuken.

$2 1/2 // 1/6 = 5/2 // 1/6 = 15/6 // 1/6$ . Je kunt nu zien dat $1/6$ precies 15 keer in $2 1/2$ past.

Je kunt de deling ook uitvoeren door beide breuken te vermenigvuldigen met het omgekeerde van de tweede (de noemer). Laat zien hoe.

$2 1/2 // 1/6 = 5/2 // 1/6 = (5/2 * 6/1) // (1/6 * 6/1) = (5/2 * 6/1) // 1 = 5/2 * 6/1 = 30/2 = 15$ .

Bereken nu met de hand (geef je antwoord als breuk):

$2/11 xx 3/11$

$6/121$

$3/8 * 1/4$

$3/32$

$7/10 // 2/5$

$7/10 * 5/2 = 35/20 = 7/4$

$3/8 * 1 5/6$

$33/48 = 11/16$

$5/12 // 1 7/8$

$5/12 * 8/15 = 2/9$

Je kunt met breuken rekenen. De vier basisbewerkingen zijn:

breuken optellen, je maakt ze dan eerst gelijknamig;

breuken aftrekken, je maakt ze dan eerst gelijknamig;

breuken vermenigvuldigen, door de tellers te vermenigvuldigen en de noemers te vermenigvuldigen;

breuken delen, je kunt dit doen door ze gelijknamig te maken, je kunt ook twee breuken delen door de eerste breuk te vermenigvuldigen met het omgekeerde van de tweede.

Je kunt deze bewerkingen zowel met de hand uitvoeren (zie voorbeelden) als met de rekenmachine.

Breuken optellen en aftrekken doe je door ze eerst gelijknamig te maken.

$2 1/2 + 1 1/3 = 2 + 1/2 + 1 + 1/3 = 2 + 3/6 + 1 + 2/6 = 3 + 5/6 = 3 5/6$ .

$2 1/2 - 1 1/3 = 2 + 1/2 - 1 - 1/3 = 2 + 3/6 - 1 - 2/6 = 1 + 1/6 = 1 1/6$ .

Je kunt ook je rekenmachine gebruiken bij het rekenen met breuken. Je gebruikt dan de breukentoets die er soms zo uitziet om breuken in te voeren.
Hier zie je hoe dat gaat bij $2 1/2 - 1 1/3$ :

levert meteen $1 1/6$ op.

Bekijk de optelling $3 1/6 + 1 1/4$ .

Doe deze berekening met de hand en controleer hem met je rekenmachine.

Handmatig: $3 2/12 + 1 3/12 = 4 5/12$ .

Doe deze optelling ook op je rekenmachine zonder de breukentoets te gebruiken.

$3 1/6 + 1 1/4$ voer je in als $3 + 1//6 + 1 + 1//4$ .
Je krijgt alleen een antwoord in oneindig veel decimalen.

Bekijk de aftrekking $3 1/6 - 1 1/4$ .

Doe deze berekening met de hand en controleer hem met je rekenmachine.

Handmatig: $3 2/12 - 1 3/12 = 38/12 - 15/12 = 23/12 = 1 11/12$ .

Doe deze aftrekking ook op je rekenmachine zonder de breukentoets te gebruiken.

$3 1/6 + 1 1/4$ voer je in als $3 + 1//6 - (1 + 1//4)$ .
Je krijgt alleen een antwoord in oneindig veel decimalen.

Oefen het optellen en aftrekken van breuken via het practicum.

Oefen tot je (bijna) geen fouten meer maakt.

Soms zijn er ook helen betrokken bij de vermenigvuldiging. Die werk je dan eerst weg.

$2 1/7 xx 5 3/4$ doe je zo:

$2 1/7 = 2 + 1/7 = 14/7 + 1/7 = 15/7$ .

$5 3/4 = 5 + 3/4 = 23/4$ .

$15/7 xx 23/4 = 345/28 = 12 9/28$ .

Kijk ook hoe dit met je rekenmachine gaat.

Bekijk de vermenigvuldiging $3 1/6 xx 1 1/4$ .

Breng die vermenigvuldiging in beeld met behulp van een rechthoek van $3 1/6$ bij $1 1/4$ .

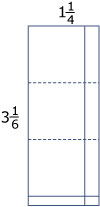
Leg met behulp van die rechthoek uit waarom je niet gewoon $3 xx 1$ en $1/6 xx 1/4$ kunt uitrekenen en dit bij elkaar optellen.

Behalve een rechthoek van $3$ bij $1$ en een rechthoekje van $1/6$ bij $1/4$ , heb je nog twee andere rechthoeken die ook meetellen.

Bepaal de juiste uitkomst met behulp van je figuur.

$3 xx 1 + 1/6 xx 1/4 + 3 xx 1/4 + 1 xx 1/6 = 95/24 = 3 23/24$ .

Bepaal de juiste uitkomst nog eens door eerst de gehelen weg te werken.

$19/6 xx 5/4 = 95/24 = 3 3/24$ .

Oefen het vermenigvuldigen van breuken via het practicum.

Oefen tot je (bijna) geen fouten meer maakt.

Breuken delen kan door ze eerst gelijknamig te maken:

$2/5 // 3/7 = 14/35 // 15/35 = 14/15$ .

$1 2/5 // 2 3/7 = 7/5 // 17/7 = 49/35 // 85/35 = 49/85$ .

Breuken delen kan ook door ze te vermenigvuldigen met het omgekeerde van de tweede breuk:

$2/5 // 3/7 = (2/5 * 7/3) // (3/7 * 7/3) = 2/5 * 7/3 = 14/15$ .

$1 2/5 // 2 3/7 = 7/5 // 17/7 = 7/5 * 7/17 = 49/85$ .

Dit kan ook op de rekenmachine met behulp van de breukentoets.
$1 2/5 // 2 3/7$ gaat dan zo:

Bekijk de deling $5/6 // 1/4$ .

Doe deze berekening met de hand en controleer hem met je rekenmachine. Kies de methode die je het handigst vindt.

$5/6 // 1/4 = 10/12 // 3/12 = 10/3 = 3 1/3$ of $5/6 // 1/4 = 5/6 * 4/1 = 20/6 = 3 1/3$ .

Welke vraag beantwoord je met deze deling?

Bijvoorbeeld: Hoeveel keer past 1/4 deel in 5/6 deel?

Bekijk de deling $3 1/6 // 1 3/4$ .

Doe deze berekening met de hand en controleer hem met je rekenmachine. Kies de methode die je het handigst vindt.

$3 1/6 // 1 3/4 = 38/12 // 21/12 = 38/21 = 1 17/21$ of $3 1/6 // 1 3/4 = 19/6 * 4/7 = 76/42 = 1 17/21$ .

Oefen het delen van breuken via het practicum.

Oefen tot je (bijna) geen fouten meer maakt.

Voer de volgende berekeningen handmatig uit. Controleer de antwoorden met de rekenmachine.

$\frac{3}{5} + 2 \frac{1}{3} = ...$

$2 14/15$

$2 \frac{1}{6} + 1 \frac{3}{4} - 2 \frac{1}{12} = ...$

$22/12 = 1 5/6$

$3 \frac{7}{12} - 2 \frac{5}{6} + \frac{2}{3} = ...$

$17/12 = 1 5/12$

$4 \frac{3}{10} - 2 \frac{2}{5} + \frac{17}{20} = ...$

$11/4 = 2 3/4$

In een stad is $1//3$ deel van mannen boven de 40 jaar en $1//7$ deel van de vrouwen boven de 40 jaar. Er zijn evenveel mannen als vrouwen.

Welk deel van mensen in die stad is boven de 40 jaar?

$1//3$ deel van de mannen is ongeveer $1//6$ deel en $1//7$ deel van de vrouwen is ongeveer $1//14$ deel van de totale bevolking. $1/6 + 1/14 = 5/21$ deel.

Waarom kun je het antwoord bij a alleen berekenen omdat er evenveel mannen als vrouwen in deze stad wonen?

Beide breuken gaan niet over hetzelfde geheel en dus kun je ze niet zonder meer optellen. Je moet eerst bekijken welk deel van het geheel ze vormen en dat kan hier alleen omdat de mannen en de vrouwen elk de helft van het geheel zijn.

Anneke, Henk en Frits verdelen een taartje.
Vreetzak Frits neemt $2/3$ deel van de taart, Anneke snijdt (bescheiden als ze is) $1/12$ deel van de taart af.

Welk deel van de taart blijft er over voor Henk?

$1 - 2/3 - 1/12 = 3/12 = 1/4$ deel.

Voer de volgende berekeningen handmatig uit. Controleer de antwoorden met de rekenmachine.

$3/5 xx 2 1/3 = ...$

$7/5 = 1 2/5$

$2 1/6 xx 1 3/5 = ...$

$104/30 = 52/15 = 3 7/15$

$3 7/12 xx 2 5/6 = ...$

$731/72 = 10 11/72$

$3/10 xx 3 1/3 = ...$

$1$

Je kunt het land van boer Groot Koerkamp voorstellen door een rechthoek. Als de boer sterft wordt het land verdeeld onder zijn zonen. Bart krijgt de helft, Dirk $3/8$ en Ben $1/8$ deel.

Geef met drie kleuren aan wie van de zonen welk deel krijgt.

Kies zelf de afmetingen van je rechthoek.

Bart verbouwt op $1/4$ deel van zijn land tulpen, op de helft narcissen en op de rest hyacinten. Dirk verbouwt op zijn stuk voor de helft tulpen en de rest hyacinten en Ben verbouwt alleen maar narcissen.

Deel de vakken op en geef in elk vakje met een T, een N of een H aan welke soort bloemen er verbouwd wordt.

Het is handig om de rechthoek in $16$ stroken te verdelen.

Op welk deel van het totale land staan tulpen?

$5/16$ deel.

Schrijf de berekening op waarmee je het deel tulpen kunt berekenen zonder het plaatje te gebruiken.

Bart: $1/4 xx 1/2 = 1/8$ . Dirk: $3/8 xx 1/2 = 3/16$ . Totaal: $1/8 + 3/16 = 5/16$ deel.

Bereken op welk deel narcissen staan en controleer het in de tekening.

Bart: $1/2 xx 1/2 = 1/4$ . Ben: $1/8$ . Totaal: $1/4 + 1/8 = 3/8$ deel.

Bereken het deel hyacinten.

Hyacinthen: $1 - 5/16 - 3/8 = 5/16$ deel.

Voer de volgende berekeningen handmatig uit. Controleer de antwoorden met de rekenmachine.

$12 // 2/3 = ...$

$18$

$2/3 // 12 = ...$

$1/18$

$3/5 // 2/3 = ...$

$9/10$

$2 1/6 // 1 3/5 = ...$

$65/48 = 1 17/48$

$3 7/12 // 2 5/6 = ...$

$43/34 = 1 9/34$

$3/10 // 3 1/3 = ...$

$9/100$

Nathalie heeft vaak last van benauwdheid. Daarom slikt ze medicijnen. Ze slikt per dag $1 1/2$ tablet. In een strip zitten $20$ tabletjes.

Hoeveel dagen doet Nathalie met één strip?

$20 // 1 1/2 = 40/3 = 13 1/3$ , dus ruim $13$ dagen.

In de zomer moet ze een $1/4$ tablet meer nemen.

Hoeveel dagen doet ze nu met één strip?

$20 // 1 3/4 = 11 3/7$ , dus ruim $11$ dagen.

Ton en Hans hebben samen een werkruimte op het computernetwerk om aan hun project te werken. Ton neemt de helft van de ruimte in gebruik, Hans heeft $3/8$ deel in gebruik.

Samen gebruiken ze dan $1/2 + 3/8 = 7/8$ deel van de totale werkruimte.
Ton gebruikt $1/2 - 3/8 = 1/8$ deel van de werkruimte meer dan Hans.
Als Ton $3/4$ deel van zijn opslagruimte heeft gevuld met data, dan heeft hij $3/4 xx 1/2=3/8$ deel van de totale werkruimte gebruikt.

Dit is een voorbeeld van het toepassen van rekenen met breuken.

Van een ICT team kan teamlid A de NAW gegevens van een database die niet te kopiëren is, in $5$ uur overnemen. Teamlid B kan dit in $3$ uur.

Welk deel van database kunnen beide teamleden samen in een uur overnemen?

Teamlid A neemt per uur $1/5$ deel van de database over.
Teamlid B neemt per uur $1/3$ deel van de database over.
Samen nemen ze per uur $1/5 + 1/3 = 8/15$ deel van de database over.

Waarom moet het steeds over dezelfde database gaan en kun je niet het overnemen van de NAW gegevens van twee verschillende databases vergelijken?

Omdat je dan de breuken niet zinvol kunt optellen.

Hoeveel tijd hebben de teamleden samen nodig om de NAW gegevens over te nemen?

Ze verwerken $8/15$ deel van de database in een uur, dus in $15$ uur verwerken ze $8$ van die databases. Per database hebben ze $15/8 = 1,875$ uur nodig.

Teamlid C neemt de NAW gegevens over in $3,5$ uur. Welk deel van de database nemen A en C over in $1$ uur? Hoeveel tijd hebben ze nodig voor de hele database?

$1/5 + 1/(3,5) = 1/5 + 2/7 = 17/35$ deel van de database over in $1$ uur. Ze hebben voor de database $17/35$ uur nodig om alle gegevens over te nemen.

Beantwoord de vragen uit d ook voor alle drie de teamleden samen.

$1/3 + 1/5 + 2/7 = 86/105$ deel van de database per uur, dus $105/86 = 1 19/86$ uur voor de NAW gegevens van de database.

Stel dat $1$ op de $8$ werkende Nederlanders werkt bij een ict-bedrijf. En ook dat daarvan $2/10$ deel op kantoor werkt.

Welk deel van alle werkende Nederlanders werkt dan bij een ict-bedrijf op kantoor?

Je moet nu $2/10$ deel van $1/8$ deel uitrekenen: $2/10 xx 1/8 = 2/80 = 1/40$ .

Dus $1$ op de $40$ werkende Nederlanders zit dan bij een ict-bedrijf op kantoor.

In een stad bestaat $3/5$ deel van de beroepsbevolking uit mannen van 20 jaar of ouder. Van die mannen is ongeveer $1$ op de $40$ werkeloos.

Welk deel van de beroepsbevolking bestaat uit werkeloze mannen van 20 jaar of ouder?

$1/40 xx 3/5 = 3/200$ deel.

Deze stad heeft op het moment een beroepsbevolking van $86text(.)315$ mensen. Hoeveel werkeloze mannen van 20 jaar of ouder zijn er?

$3/200 xx 86315 ~~ 1295$ mannen.

Bereken met de hand en controleer achteraf met je rekenmachine.

$1 2/3+5 4/5$

$7 7/15$

$1 2/3+5 4/5=1 10/15+5 12/15=6 22/15=7 7/15$

$2 7/8-3/10$

$2 23/40$

$2 7/8-3/10=2 70/80-24/80=2 46/80=2 23/40$

Bereken zonder rekenmachine.

$2 1/3 xx 4 2/5$

$154/15=10 4/15$

$2 1/3 xx 4 2/5=7/3 xx 22/5=154/15=10 4/15$

$1/3 //4 2/8$

$4/51$

$(1/3)/(4 2/8)=(1/3)/(34/8)=(8/24)/(102/24)=8/102=4/51$

$3 3/8 xx 1/4$

$27/32$

$3 3/8 xx 1/4=27/8 xx1/4=27/32$

$1/7//2/3$

$3/14$

$(1/7)/(2/3)=(3/21)/(14/21)=3/14$

$2/5 xx2 4/7$

$36/35=1 1/35$

$2/5 xx 2 4/7=2/5 xx 18/7=36/35=1 1/35$

$4 1/4//2 1/8$

$34/17=2$

$(4 1/4)/(2 1/8)=(17/4)/(17/8)=(34/8)/(17/8)=34/17=2$

Neem aan dat in een bepaald gebied vier op de zes leerlingen naar het mbo gaat. Van deze leerlingen kiest $1/4$ de richting zorg en welzijn, $2/3$ gaat voor techniek en de rest kiest economie.

Het hoeveelste deel van deze mbo-leerlingen kiest voor economie?

$1/12$

$1- 2/3 - 1/4=1/12$

Welk deel van de leerlingen in dit gebied gaat naar zorg en welzijn op het mbo?

$1/6$

$4/6 xx 1/4=4/24=1/6$

Op een scholengemeenschap in dit gebied zitten $1500$ leerlingen.
Hoeveel van hen kiezen voor techniek op het mbo?

$666 2/3 ~~ 667$ leerlingen.

$4/6 xx 2/3=8/18=4/9$ deel gaat voor techniek. $4/9 xx 1500=666 2/3 ~~ 667$ leerlingen.

Met AlgebraKIT kun je oefenen met het rekenen met breuken. Je kunt telkens een nieuwe opgave oproepen. Je maakt elke opgave zelf op papier.
Met Toon uitwerking zie je het verder uitklapbare antwoord.
Met krijg je een nieuwe opgave.