de begrippen macht, grondtal, exponent, machtsverheffen;

rekenen met machten in de juiste rekenvolgorde.

rekenen met positieve en negatieve decimale getallen met de juiste rekenvolgorde;

rekenen met breuken.

Als je een A4-blaadje dubbelvouwt, krijg je twee lagen papier.
Als je het blad nog een keer dubbelvouwt, krijg je vier lagen papier.
Hoeveel lagen papier krijg je als je het blad tien keer hebt dubbelgevouwen?

$1024$ lagen.

$2xx2xx2xx2xx2xx2xx2xx2xx2xx2 =2^10 = 1024$ lagen.

Je krijgt een kwadraat als je een getal met zichzelf vermenigvuldigt: $3 * 3 = 3^2$ .

Je krijgt een macht als je met steeds hetzelfde getal vermenigvuldigt: $3 * 3 * 3 * 3 * 3 = 3^5$ .
Reken je zo'n getal uit, dan wordt de uitkomst machtig groot: $3^5 = 243$ .

Je spreekt van machtsverheffen en je zegt 3 tot de macht 5, of kortweg 3 tot de vijfde. $3^5$ is een macht met grondtal $3$ en exponent $5$ .
Een kwadraat zoals $3^2$ is een macht met grondtal $3$ en exponent $2$ .

Je kunt ook de machten berekenen van een breuk: $(2/5)^3=2/5*2/5*2/5=8/125$

Je kunt ook de machten berekenen van negatieve getallen. Let op de rekenvolgorde: $text(-)17^3= text(-)17*17*17= text(-)4913$ en $( text(-)17)^3= text(-)17* text(-)17* text(-)17= text(-)4913$

Verder zijn er rekenregels:

machten vermenigvuldigen dan exponenten optellen:
$10^4 * 10^3 = 10*10*10*10\ *\ 10*10*10 = 10^7$ ;

machten delen dan exponenten aftrekken:
$10^5 // 10^3 = (10*10*10*10*10) // (10*10*10) = 10^2$ ;

machten van machten dan exponenten vermenigvuldigen:
$(10^3)^4 = 10^3 * 10^3 * 10^3 * 10^3 = 10^12$ ;

grondtal niet $0$ en exponent wel: $10^0 = 1$ ;

negatieve exponenten kunnen ook voorkomen:
$10^3 // 10^5 = (10*10*10) // (10*10*10*10*10) = 1/(10^2) = 10^(text(-)2)$ ;

machten gaan in een berekening voor vermenigvuldigen en delen.

Het samennemen of korter schrijven van machten heet herleiden.

Bereken de machten.

$1^12$

$1$

$1·1·1·1·1·1·1·1·1·1·1·1=1$

$3,5^3$

$42,875$

$3,5·3,5·3,5=42,875$

$( 1/3 ) ^4$

$1/81$

$1/3·1/3·1/3·1/3=1/81$

$( 2/5 ) ^4$

$16/625$

$2/5·2/5·2/5·2/5=16/625$

Bereken $3^4$ .

$81$

$3*3*3*3=81$

Wat betekent $(text(-)3) ^4$ ? Wat is de uitkomst?

$( text(-)3 ) ^4 = text(-)3 * text(-)3 * text(-)3 *text(-)3=81$

Wat betekent $text(-)3^4$ ? Wat is de uitkomst?

$text(-)3^4 = text(-)3 * 3 * 3 * 3 = text(-)81$

Bereken.

$( 1/2 ) ^4$

$1/16$

$1/2 * 1/2 * 1/2 * 1/2 = 1/16$

$( 2 2/3 ) ^3$

$18 26/27$

$8/3 * 8/3 * 8/3=512/27=18 26/27$

$( 2/7 ) ^0$

$1$

$text(-)2 * ( text(-)3 ) ^2$

$text(-)18$

$text(-)2*text(-)3*text(-)3=text(-)18$

Herleid de machten. Je hoeft ze niet te berekenen.

$3^95 * 3^114$

$3^95 * 3^114 = 3^209$

$3^114/3^95$

$3^114/3^95 = 3^19$

$( 3^12 ) ^5$

$( 3^12 ) ^5 = 3^60$

$( 3^15 ) ^10/ (3^50 * 3^100)$

$1$

$( 3^15 ) ^10/ (3^50 * 3^100) =3^150/3^150= 3^0 = 1$

Je krijgt een macht als je met steeds hetzelfde getal vermenigvuldigt: $3 * 3 * 3 * 3 * 3 = 3^5$ .

Rekenregels om machten te herleiden:

machten vermenigvuldigen dan exponenten optellen: $10^4 * 10^3 = 10^7$ ;

machten delen dan exponenten aftrekken: $10^5 // 10^3 = 10^2$ ;

machten van machten dan exponenten vermenigvuldigen: $(10^3)^4 = 10^12$ ;

grondtal niet $0$ en exponent wel: $10^0 = 1$ ;

negatieve exponenten kunnen ook voorkomen: $10^3 // 10^5 = 1/(10^2) = 10^(text(-)2)$ ;

machten gaan in een berekening voor vermenigvuldigen en delen.

Bij het rekenen moet je machten berekenen voor vermenigvuldigen en delen.

Met haakjes kun je de volgorde beïnvloeden: wat daarbinnen staat doe je eerst. Hier zie je een voorbeeld van hoe je dit kunt toepassen.

$2 * 2^4 + 2 *3 -4 *(2 +6 )/(2^3)$
$=2 *16 +2 *3 -4 *8/8$
$=32+2 *3 -4 *8/8$
$=32+6 -4$
$=34$

Let goed op mintekens en haakjes: $(text(-)17) ^4 = text(-)17 * text(-)17 * text(-)17 *text(-)17 = 83521$ , maar $text(-)17^4 = text(-)17 * 17 * 17 * 17 = text(-)83521$ .

Let op de rekenvolgorde en bereken.

$4 *2^5-400 /(2^4)$

$4 *32 - 400 /(16 )= 103$

$((2^3+3^2)^2)/17 - 2^2$

$((8+9)^2)/17 - 4 = 17 - 4 = 13$

$(2 * 1/(2^3)) ^3$

$(2*1/8)^3 = (1/4)^3 = 1/64$

Bereken.

$500- text(-)5^3$

$500- text(-)5*5*5=625$

$500- (text(-)5)^3$

$500- text(-)5*text(-)5*text(-)5= 625$

$500+text(-)5^4$

$500+text(-)5*5*5*5=text(-)125$

$500+(text(-)5)^4$

$500+text(-)5*text(-)5*text(-)5*text(-)5=1125$

Soms kun je uitdrukkingen met machten berekenen door eerst te herleiden

Bereken: $(17^304 * 17^98)/((17^100)^4)$

$(17^304 * 17^98)/((17^100)^4) = (17^402)/(17^400) = 17^2 = 289$

Bereken.

$(13^240)/((13^10)^4 * 13^200)$

$(13^240)/((13^10)^4 * 13^200) = (13^240)/(13^40 * 13^200) = 1$ .

$(4^99)/(2^150 * (text(-)2^5)^10)$

$(4^99)/(2^150 * (text(-)2^5)^10) = ((2^2)^99)/(2^150 * 2^50) = (2^198)/(2^200) = 1/(2^2) = 1/4$ .

Reken je met getallen in de technische notatie dan werk je met machten.

Een raket wordt afgeschoten met een snelheid van $42 * 10^3$ km/h richting de maan.
Hij moet een afstand afleggen van ongeveer $1,20*10^6$ km.
Hoe lang is de raket onderweg?

$1,20*10^6 // 42*10^3 = 1,20 // 42 *10^3 ~~ 28,6$ uur.

Er zitten ongeveer $6,02 * 10^23$ atomen in $12$ gram 12C (koolstof).
Hoeveel gram weegt $1$ atoom van deze koolstof? Geef je antwoord in drie significante cijfers in de technische notatie.

$12 // (6,02*10^23) ~~ 1,99 * 10^(text(-)23) ~~ 19,9 * 10^(text(-)24)$ gram.

Bereken.

$4^5$

$4^5 = 1024$

$3^4 * 2^3$

$3^4 * 2^3 = 648$

$3^4 * 2^3 = 81 *8 = 648$

$( 2/3 ) ^4$

$( 2/3 ) ^4 = 16/81$

$( 1 3/5 ) ^3$

$( 1 3/5 ) ^3 = 4 12/125$

$( 1 3/5 ) ^3 = ( 8/5 ) ^3 = 512/125 = 4 12/125$

$( text(-)2 ) ^6$

$( text(-)2 ) ^6 = 64$

$text(-)2^4 * 3^3$

$text(-)2^4 * 3^3 = text(-)432$

$text(-)2^4 * 3^3 = text(-)16 * 27 = text(-)432$

Vul de kruisgetallenpuzzel in.

Horizontaal		Verticaal
1	(6^2)^3	1	2^4*5^2+1
4	3^2*(2^2)^2	2	((23)^2)(20-1)
6	(3^7)/(3^5)*10	3	2*5^5
7	2*10^3+2	5	10*((7^5)/(7^3) -1)
		6	(2^3)^2*3-10^2

Herleid de machten. Je hoeft ze niet te berekenen.

$2^16 * ( 2^10 ) ^3$

$2^16 * ( 2^10 ) ^3 = 2^46$

$2^16 * ( 2^10 ) ^3 = 2^6*2^30=2^46$

$(4 * 2^26) /2^20$

$(4 * 2^26) /2^20 = 2^8$

$(4 * 2^26) /2^20 = (2^2*2^26)/2^20=2^28/2^20=2^8$

$(2^14 * 2^26) /( 2^20 ) ^2$

$(2^14 * 2^26) /( 2^20 ) ^2 = 2^0 = 1$

$(2^14 * 2^26) /( 2^20 ) ^2 = 2^40/2^40= 2^0 = 1$

Alle stoffen bestaan uit atomen. Die atomen hebben een zekere massa, de atoommassa. Die atoommassa wordt uitgedrukt in een eenheid u die gelijk is aan eentwaalfde deel van een koolstof-12 atoom, namelijk $1,66 * 10^(text(-)24)$ gram.

Het koolstof-12 atoom heeft dus een massa van $12$ u. Hoeveel gram is dat?

$12 * 1,66 * 10^(text(-)24) = 19,92 * 10^(text(-)24) ~~ 1,99 * 10^(text(-)23)$ gram.

Uit hoeveel atomen bestaat $12$ gram koolstof-12?

Uit ongeveer $(12)/(1,99 * 10^(text(-)23) ~~ 6,02 * 10^(23))$ atomen. (Dit getal is de constante van Avogadro.)

Waterstof heeft een atoommassa van ongeveer $1$ u en zuurstof van ongeveer $16$ u.

Laat zien dat $1$ gram waterstof en $16$ gram zuurstof evenveel atomen bevatten.

Allebei ongeveer $6,02 * 10^23$ atomen.

Water heeft moleculen die bestaan uit $1$ atoom zuurstof en $2$ atomen waterstof. De molecuulmassa is daarom $18$ u.

Hoeveel moleculen zitten er in $1$ kg (dat is $1$ liter) water?

Ongeveer $(10^3)/(18 * 1,66 * 10^(text(-)24)) ~~ 3,35 * 10^25$ .

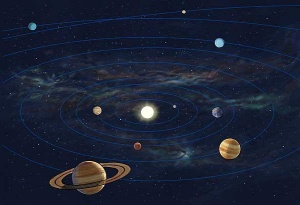
De astronomische eenheid (AE) is de gemiddelde afstand van de aarde tot de zon. $1$ AE $~~ 150 * 10^6$ km.

Hoeveel AE is $1$ km?

$1/(150*10^6) ~~ 6,7*10^(text(-)9)$ AE. (Denk er om dat je antwoorden ook in de technische notatie moeten staan en dat veel decimalen of exacte waarden nu onzinnig zijn.)

Planeet Jupiter bevindt zich ongeveer $5,2$ AE van de zon. Hoeveel km is dat?

$5,2*150*10^6 = 780*10^6$ km.

Pluto bevindt zich ongeveer $5,9 * 10^9$ km van de zon. Hoeveel AE is dat?

$(5,9*10^9)/(150*10^6) ~~ 39$ AE.

Een lichtjaar is de afstand die het licht in een jaar aflegt. De lichtsnelheid is $300 * 10^6$ m/s. Hoeveel AE is $1$ lichtjaar?

Het licht legt in een jaar ongeveer $365 * 24 * 60 * 60 * 300*10^6 // 1000 ~~ 9,46*10^12$ km af. Dat is ongeveer $63072$ AE.

Sissah Ben Dahir is de uitvinder van het schaakspel. De Indiase koning Shirham vroeg hem wat hij als beloning voor die uitvinding wilde hebben. Sissah Ben Dahir zei: Geef me één graankorrel om op het eerste veld van het bord te leggen, 2 graankorrels voor op het tweede veld, 4 voor op het derde veld, 8 op het vierde en laat me zo verder gaande alle 64 velden bedekken.
De koning lachte en antwoordde: Is dat echt alles dat je wilt hebben? en hij gaf opdracht het graan uit te betalen. Toen bleek dat de koning te weinig graan had om Sissah uit te betalen, liet hij hem in de gevangenis opsluiten.

Bekijk het verhaal dat wordt beschreven in Toepassen.
Je ziet in de figuur hoeveel vakjes een schaakbord heeft.

Hoeveel graankorrels moet de koning op het tiende vakje leggen?

$2^{9} = 512$

Hoeveel graankorrels komen er op het $64$ ste vakje?

$2^{63}$ .

Je rekenmachine kan het aantal graankorrels op het $64$ ste vakje niet uitrekenen, alleen benaderen. Hoeveel graankorrels worden het ongeveer?

Ongeveer $9,22 * 10^18$ .

Neem aan dat een graankorrel ongeveer $65$ mg weegt.

Hoeveel gewicht zou er dan op het $64$ ste vakje rusten als alle graankorrels er op zouden kunnen liggen?

Ongeveer $0,065 * 9,22 * 10^18 = 0,5993 * 10^18 ~~ 5,99 * 10^17$ gram en dat is ongeveer $5,99 * 10^14 ~~ 599 * 10^12$ kg.

Neem aan dat een vakje van het schaakbord $5$ bij $5$ cm is en dat in elke cm3 zo'n $100$ graankorrels kunnen worden geperst. De hoeveelheid graan op het $64$ ste vakje past dan in een balkvormige toren met een grondvlak van $5$ bij $5$ cm.

Hoe hoog zou die toren moeten worden?

Je moet er $9,22 * 10^16$ cm3 graan in kwijt kunnen. De hoogte wordt dan $9,22 * 10^16 // 25 = 3,69 * 10^15$ cm en dat is $3,69 * 10^10$ km oftwel $36,9$ miljard km.

Bekijk nog eens het verhaal dat wordt beschreven in Toepassen.
Je ziet in de figuur hoeveel vakjes een schaakbord heeft.

Hoeveel graankorrels moet de koning op de eerste tien vakjes samen leggen?

$1 + 2 + 2^{2} + 2^{3} + 2^{4} + 2^{5} + 2^{6} + 2^{7} + 2^{8} + 2^{9} = 1023$

Laat zien dat het antwoord op de vorige vraag gelijk is aan $2^{10} - 1$ .

Daar komt ook $1023$ uit.

De totale hoeveelheid graankorrels die op het schaakbord zouden moeten komen is $1 + 2 + 2^{2} + 2^{3} + ... + 2^{62} + 2^{63}$ . Dit is gelijk aan $2^{64} - 1$ .

Dat kun je zelf beredeneren. Probeer die redenering te vinden.

Stel $s = 1 + 2 + 2^{2} + 2^{3} + ... + 2^{62} + 2^{63}$ , dan is $2 s = 2 + 2^{2} + 2^{3} + ... + 2^{62} + 2^{63} + 2^{64}$ . Daaruit volgt $s = 2 s - s = 2^{64} - 1$ .

Bereken uit het hoofd.

$2^7$

$2^7=128$

$(text(-)2)^7$

$(text(-)2)^7=text(-)128$

$text(-)2^7$

$text(-)2^7=text(-)128$

$(2/3)^4$

$(2/3)^4=16/81$

Bereken de macht met grondtal $3$ en exponent $6$ .

$3^6=729$

Bereken.

$text(-)4*2^3-(3/4)^3$

$text(-)4*2^3-(3/4)^3=text(-)32 27/64$

$text(-)4*2^3-(3/4)^3=text(-)4*8-27/64=text(-)32-27/64=text(-)32 27/64$

$text(-)2*(text(-)4)^4$

$text(-)2*(text(-)4)^4=text(-)512$

$text(-)2*(text(-)4)^4=text(-)2*256=text(-)512$

$(2/4)^3*3+2^6$

$(2/4)^3*3+2^6=64 3/8$

$(2/4)^3*3+2^6=1/8 *3+64=3/8+64=64 3/8$

$text(-)4^4+3^5*2^2$

$text(-)4^4+3^5*2^2=716$

$text(-)4^4+3^5*2^2=text(-)256+243*4=text(-)256+972=716$

Herleid de volgende machten. Je hoeft ze niet uit te rekenen.

$(9^20)^4/(3^2*9^16)$

$(9^20)^4/(3^2*9^16)=9^63$

$(9^20)^4/(3^2*9^16)=9^80/9^17=9^63$

$6^16*6^12$

$6^16*6^12=6^28$

$(4^17)^4$

$(4^17)^4=4^68$

$12^14*12^80/12^56$

$12^14*12^80/12^56=12^38$

$12^14*12^80/12^56=12^14*12^24=12^38$

Met AlgebraKIT kun je oefenen met het rekenen met machten. Je kunt telkens een nieuwe opgave oproepen. Je maakt elke opgave zelf op papier.
Met Toon uitwerking zie je het verder uitklapbare antwoord.
Met krijg je een nieuwe opgave.