het begrip ongelijkheid en ongelijkheden systematisch oplossen.

werken met breuken in formules en vergelijkingen;

grafieken tekenen bij formules;

formules herleiden en vergelijkingen oplossen met de basismethoden.

Je rijdt met de auto $16$ km over de snelweg. Je hebt een constante (gemiddelde) snelheid. Maar je moet onderweg wel even stoppen om te tanken en dat kost $5$ minuten.

Als je $16$ km met $120$ km/uur rijdt, hoe lang doe je daar dan over? Geef je antwoord eerst in uren en dan in minuten.

$16 /120 =2/15$ uur en dus $8$ minuten. Daar komt nog $5$ minuten bij voor het tanken, totaal dus $13$ minuten.

Als je $16$ km met $60$ km/uur rijdt, hoe lang doe je daar dan over? Geef je antwoord eerst in uren en dan in minuten.

$16 /60 =4/15$ uur en dus $16$ minuten. Daar komt nog $5$ minuten bij voor het tanken, totaal dus $21$ minuten.

Noem de snelheid in km/uur $v$ en de reistijd in uren $t$ .
Bij welke snelheid is de reistijd meer dan $15$ minuten?

Laat zien, dat bij deze vraag de ongelijkheid $16/v+1/12 gt 1/4$ hoort.

Het tanken kost $5/60=1/12$ uur.
Een mogelijke formule voor de reistijd is $t=16/v+1/12$ .
$15$ minuten is $1/4$ uur, dus $16/v+1/12 gt 1/4$ .

Hoe los je deze ongelijkheid op?

Teken een grafiek van $t=16/v+1/12$ .
Los vervolgens op: $16/v+1/12 = 1/4$ .
Dit geeft $v = 96$ km/uur, dus (zie grafiek) je moet minder dan $96$ km/uur rijden gemiddeld.

Je rijdt weer op de Afsluitdijk, die $32$ km lang is. Je stapt dit keer onderweg $5$ minuten uit om van het uitzicht te genieten. Je ziet dat je de reistijd $t$ in minuten kunt berekenen door de afstand van $32$ km te delen door de snelheid $v$ (km/h), met $60$ te vermenigvuldigen en ten slotte nog $5$ bij de uitkomst op te tellen:

$t=32/v*60 + 5 =1920/v+5$

Bij deze formule kun je een bijbehorende grafiek tekenen.

Voor snelheden dicht bij $0$ wordt de reistijd heel erg groot, de grafiek loopt omhoog tot vlak bij de verticale as. Zo´n lijn waar de grafiek steeds dichter naartoe loopt heet een asymptoot.
Voor hele grote snelheden komt de reistijd in de buurt van de $5$ minuten. Maar wanneer is de reistijd bijvoorbeeld langer dan $60$ minuten?

Daarbij hoort de ongelijkheid: $1920/v+5 gt 60$ .

Om een ongelijkheid op te lossen bekijk je altijd de bijbehorende grafieken. In dit geval zijn dat de grafiek van $t=1920/v+5$ en de lijn $t = 60$ .

In het snijpunt van beide grafieken is $1920/v+5 = 60$

De waarde van $v$ die daarbij hoort bereken je: $v ~~ 34,91$ km/uur.

Uit de grafiek lees je vervolgens de oplossing van de ongelijkheid af: $v le 34,9$ km/uur.

Je rijdt $32$ km over de snelweg en je stopt onderweg $5$ minuten om te tanken.

Hoeveel minuten doe je over deze $32$ km als je $80$ km/h rijdt?

$29$ minuten

$32 /80 *60 +5 =29$ minuten

Hoeveel minuten doe je daarover als je $40$ km/h rijdt?

$53$ minuten

$32 /40 *60 +5 =53$ minuten

Teken zelf de grafiek van $t=1920/v+5$ . Maak eerst een tabel met voor $v$ de waarden $10$ , $20$ , ..., $120$ .

$v$	10	20	30	40	50	60	70	80	90	100	110	120
$t$	197	101	69	53	43,4	37	32,4	29	26,3	24,2	22,5	21

Wat betekent het voor de reistijd als je snelheid bijna $0$ wordt? Wat betekent dit voor de grafiek?

Je reistijd wordt dan heel erg groot. De grafiek gaat dus in de buurt van de verticale $t$ -as heel sterk omhoog.

Wat betekent het voor de reistijd als je snelheid heel groot wordt? Wat betekent dit voor de grafiek?

Je reistijd benadert dan de $5$ minuten. De grafiek gaat dus voor grote waarden van $v$ vlak boven de horizontale lijn $v=5$ lopen.

Bekijk de Uitleg.
Je wilt de ongelijkheid $1920/v+5 gt 60$ oplossen.

Laat zien hoe je $1920/v+5 = 60$ exact kunt oplossen.

Met de balansmethode:

$1920/v+5$

$=$

$60$

beide zijden $- 5$

$1920/v$

$=$

$55$

beide zijden $xx v$

$1920$

$=$

$55v$

beide zijden $// 55$ en omwisselen

$v$

$=$

$1920/55$

Lees vervolgens de juiste exacte oplossing van de ongelijkheid uit de grafiek af.

$v lt 1920/55$ km/uur.

Geef vervolgens je antwoord in km/uur in één decimaal nauwkeurig.

$v lt 1920/55 = 34,9090...$ km/uur en dus is $v le 34,9$ km/uur.

Los de volgende ongelijkheden op.
Schets de bijbehorende grafieken en los de bijbehorende vergelijkingen exact op. Neem aan dat $x gt 0$ .

$2/x + 3 lt 7$

$2/x + 3 = 7$ geeft $2/x = 4$ en dus $x = 0,5$ .
Uit de grafiek lees je af: $x gt 0,5$ .

$2/x + 3 le 15$

$2/x + 3 = 15$ geeft $2/x = 12$ en dus $x = 1/6$ .
Uit de grafiek lees je af: $x ge 1/6$ .

$1/x lt x$

$1/x = x$ geeft $x^2 = 1$ en dus $x = 1$ (omdat $x gt 0$ ).
Uit de grafiek lees je af: $x gt 1$ .

Een uitdrukking zoals $y_1 gt y_2$ , $y_1 ge y_2$ , $y_1 le y_2$ of $y_1 lt y_2$ heet een ongelijkheid. Ongelijkheden los je op met behulp van grafieken.

Eerst maak je bij de formules voor $y_1$ en $y_2$ een grafiek. Alle snijpunten moeten zichtbaar zijn!

Dan bereken je de coördinaten van de snijpunten.
Dat doe je door de vergelijking $y_1 = y_2$ op te lossen.
Probeer dat altijd exact te doen, afronden doe je als daarom wordt gevraagd.

Vervolgens lees je de oplossing van de ongelijkheid uit de grafieken af. Let daarbij goed op de gewenste nauwkeurigheid!

Voor het laten drukken van folders betaal je een vast bedrag van € 10,00 en daarbovenop € 0,04 per folder. De kosten per folder zijn daarom hoog als je maar weinig folders laat drukken.

Noem het aantal folders dat je wilt laten drukken $a$ en de kosten per folder $k$ . Maak een bijpassende formule van $k$ afhankelijk van $a$ en teken de grafiek. Je wilt niet meer dan € 0,06 per folder betalen. Hoeveel folders $a$ moet je dan laten drukken?

Per folder betaal je in ieder geval € 0,04. Verder betaal je per folder $10 /a$ euro.
In totaal dus $k=0,04 +10/a$ euro per folder.

Om een goede bijpassende grafiek te maken moet je bedenken dat je veel folders wilt laten maken om de kosten per folder laag te houden. Misschien wel zo'n $1000$ stuks. $a$ komt op de horizontale as en laat je daarom bijvoorbeeld lopen vanaf $0$ tot en met $1000$ . Voor $1000$ folders betaal je € 0,05 per stuk, maar voor $100$ folders betaal je € 0,14 per stuk. Maak zelf een goede tabel en grafiek.

Je moet vervolgens oplossen $0,04 +10/a=0,06$ . Dat kun je doen met behulp van de grafiek en inklemmen, maar je kunt ook de balansmethode toepassen. Daarna los je de hyperbolische ongelijkheid $0,04+10/a gt 0,06$ op.

Bekijk welk probleem er in het voorbeeld aan de orde wordt gesteld.

Maak een tabel (in drie decimalen nauwkeurig) en een grafiek bij de formule.

Maak een grafiek bij deze tabel. Laat de $k$ -as lopen van $0$ tot en met $0,20$ .

$a$	$0$	$100$	$200$	$300$	$400$	$500$	$600$	$700$	$800$	$900$	$1000$
$k$	-	$0,140$	$0,090$	$0,073$	$0,065$	$0,060$	$0,057$	$0,054$	$0,053$	$0,051$	$0,050$

Je wilt weten bij welk aantal folders $a$ geldt $k lt 0,06$ . Welke waarde voor $a$ levert precies $0,06$ op? En wat wordt dus je antwoord?

Je vindt met behulp van de tabel bij a, dat $k=0,06$ als $a=500$ . Het antwoord wordt $a gt 500$ .

In Voorbeeld staat dat je het antwoord bij b ook kunt vinden door te redeneren.

Leg uit hoe je dan de vergelijking $0,04 +10/a=0,06$ oplost.

Eerst aan beide zijden van het isgelijkteken $0,04$ aftrekken: $10/a=0,02$
Hieruit volgt: $a= 10/(0,02)=500$ .

Bij de productie van verf is er sprake van productiekosten per liter, maar ook van vaste kosten (machine, bedrijfshal, enzovoort) die niet van het geproduceerde aantal liter verf afhangen. Bij het berekenen van de prijs die de fabrikant per liter verf gaat berekenen moet hij ook met deze vaste kosten rekening houden. Neem aan dat die vaste kosten € $32000,00$ bedragen. De productiekosten per liter bedragen € 5,60.

Stel een formule op voor de totale kosten per liter ( $K$ in euro/liter) afhankelijk van het aantal geproduceerde liters $a$ .

$K=32000/a+5,60$

Bereken hiermee de totale kosten per liter bij een productie van $10000$ liter van deze verf.

$K=8,80$ euro

$K=32000/10000+5,60 =8,80$ euro

Bij welke waarde van $a$ worden de totale kosten per liter kleiner dan € 6,00?

$a>80000$

$6,00$

$=$

$32000/a+5,60$

$0,40$

$=$

$32000/a$

$a$

$=$

$(32000)/(0,40)$

$a$

$=$

$80000$

Dus geldt $a > 80000$ .

Los op: $1/x le x^3$ . Neem aan dat alle waarden van $x$ zijn toegestaan.

Maak eerst de grafieken van $y_1 = 1/x$ en $y_2 = x^3$ in één figuur.

Gebruik ook vervolgens de balansmethode:

$1/x$

$=$

$x^3$

beide zijden $xx x$ en omwisselen

$x^4$

$=$

$1$

beide zijden vierde machtswortel trekken

$x$

$=$

$1$ en/of $x = text(-)1$

Uit de grafieken lees je de oplossing af: $text(-)1 le x lt 0$ en/of $x ge 1$ .

In Voorbeeld zie je hoe je een ongelijkheid kunt oplossen met grafieken en de balansmethode.

Maak zelf de grafieken van $y_1=1/x$ en $y_2 = x^3$ .

Dit kun je bijvoorbeeld doen met behulp van GeoGebra, met een grafische rekenmachine of met de hand.

Leg uit hoe je aan de oplossing van de ongelijkheid komt.

$y_1$ moet kleinere (of gelijke) uitkomsten hebben als $y_2$
Dat is rechts van $x = text(-)1$ tot aan de verticale $y$ -as, maar ook rechts van $x = 1$ .
Verder horen $x = text(-)1$ en $x = 1$ bij de oplossingen, maar $x=0$ is geen toegestane waarde.

Schrijf de oplossing van de ongelijkheid $1/x gt x^3$ op.

$x lt text(-)1$ en/of $0 lt x lt 1$ .

Los de ongelijkheden op.

$1/6x+2 le 4 -1/2x$

$1/6x+2 le 4 -1/2x$ geeft $x = 3$ .
Uit de grafiek volgt $x le 3$ .

$1/6x+2$

$=$

$4 -1/2x$

$x+12$

$=$

$24 - 3x$

$4x$

$=$

$12$

$x$

$=$

$3$

Uit de grafiek volgt $x le 3$ .

$3/p+15 ge 17$

$3/p+15 = 17$ geeft $p = 1,5$ .
De oplossing is $0 lt p le 1,5$ .

$3/p+15$

$=$

$17$

$3/p$

$=$

$2$

$p$

$=$

$1,5$

Grafiek: $0 lt p le 1,5$ .

$x^2 ge 8/x$

$x^2 = 8/x$ geeft $x^3 = 8$ en dus $x = 2$ .
Uit de grafiek volgt $x ge 2$ .

$x^2$

$=$

$8/x$

$x^3$

$=$

$8$

$x$

$=$

$root[3](8) = 2$

Grafiek: $x ge 2$ .

Op veel scholen kun je ook als leerling kopieën maken. De maandelijkse kosten voor de school zijn:

de huur en het onderhoud van de kopieermachine: € 150,00

de kosten per kopie: € 0,02

Noem de maandelijkse kosten per kopie $K$ en het aantal kopieën $a$ .

Welke formule geldt voor $K$ afhankelijk van $a$ ?

$K = 150/a + 0,02$

Teken een grafiek bij deze formule.

Stel dat je als leerling € 0,05 per kopie betaalt. Hoeveel kopieën moeten er dan maandelijks minstens worden gemaakt als de school geen verlies wil draaien? Los de bijbehorende ongelijkheid systematisch op.

Eerst los je $150/a + 0,02 = 0,05$ op. Dit geeft $150/a = 0,03$ en dus $a = 5000$ .
Nu kijk je in je grafiek en je vindt $a > 5000$ . Dus bij meer dan $5000$ kopieën is de school uit de kosten.

Je wilt de ongelijkheid $4/x+2 >x+1$ oplossen.

Teken de grafieken van $y_1 =4/x+2$ en $y_2 =x+1$ in één figuur. Houd ook rekening met negatieve waarden van $x$ .

Aan de grafieken zie je dat er twee snijpunten zijn. Bereken de coördinaten van die snijpunten door inklemmen in één decimaal nauwkeurig.

Je vindt $(2,6; 3,6)$ en $(text(-)1,6; text(-)0,6)$ .

Schrijf de oplossingen van deze vergelijking op in één decimaal nauwkeurig.

De twee oplossingen zijn: $x≈ text(-) 1,6$ en $x≈2,6$

Schrijf de oplossingen van de ongelijkheid $4/x+2 >x+1$ op in één decimaal nauwkeurig.

De oplossingen zijn $x lt text(-) 1,6$ en $0 lt x lt 2,6$ .

Los de volgende ongelijkheden op. Neem aan dat $x$ alleen positieve waarden heeft.

$2400/x + 3,6 lt 6,8$

$2400/x + 3,6 = 6,8$ geeft $2400/x = 3,2$ en $x = 2400/(3,2) = 750$ .
Uit de grafieken volgt $x gt 750$ .

$200 + 50/x ge 450$

$200 + 50/x = 450$ geeft $50/x = 250$ en $x = 50/250 = 0,2$ .
Uit de grafieken volgt $0 lt x le 0,2$ .

$(x - 15) /300 - 0,5 gt 0,8$

$(x - 15) /300 - 0,5 = 0,8$ geeft $(x - 15) /300 = 1,3$ en $x - 15 = 390$ , dus $x = 405$ .
Uit de grafieken volgt $x gt 405$ .

$800/ (x - 5) ge 50$

$800/ (x - 5) = 50$ geeft $x - 5 = 800/50 = 16$ en dus $x = 21$ .
Uit de grafieken volgt $5 lt x le 21$ .

Als je een gewicht aan een touw rustig heen en weer laat slingeren (het touw moet strak blijven, dus geen al te grote uitwijking), dan is de slingertijd $T$ (in seconden) alleen afhankelijk van de lengte van het touw $l$ (in meter). De slingertijd is de tijd die het duurt voor het gewicht om precies één keer heen en weer te slingeren.
Er geldt: $T = 2pi sqrt(l/g)$ .
Hierin is $g ~~ 9,81$ de gravitatieconstante.

Je ziet dat de trillingstijd iets langzamer is dan $1$ seconde.
Hoe lang moet het touw dan minstens zijn in cm nauwkeurig?

Je moet oplossen $2pi sqrt(l/(9,81)) gt 1$ . $2pi sqrt(l/(9,81)) = 1$ geeft $l/(9,81) = (1/(2pi))^2$ en dus $l = 9,81*(1/(2pi))^2 ~~ 0,25$ m.
Grafiek: $l ge 0,25$ m.

Van een bepaald type rechthoekige verpakkingsdozen zijn lengte en breedte hetzelfde, maar is de hoogte de helft van de lengte.

Welke afmetingen moeten deze dozen hebben om er tot maximaal $0,25$ m3 ruimte in te hebben?

Noem de lengte $x$ m, dan is de breedte $x$ m en de hoogte is $1/2x$ m.
Voor het volume geldt dan $1/2 x^3 lt 0,25$ .
$1/2 x^3 lt 0,25$ geeft $x^3 = 0,5$ en dus $x ~~ 0,79$ m.
De dozen moeten $0,79 xx 0,79 xx 0,40$ m worden.

Deze hijskraan kan zware lasten tillen. De last hangt aan een katrol die langs de arm beweegt. De afstand van de plek waaronder de katrol hangt tot het steunpunt van de arm, heet de armlengte $a$ .

De grootste massa $m$ die deze kraan kan tillen, hangt af van de armlengte.
Voor deze kraan geldt: $m=120000/a$
Hierin is $m$ in kg en $a$ in meters.

In deze opgave bereken je op welke afstand van de kraan een gewicht van $6$ ton ( $6000$ kg) nog kan hangen.

Welke ongelijkheid moet er worden opgelost?

$120000/a lt 6000$

Los de bijbehorende vergelijking op.

$a=120000/6000=20$

Op welke afstand van de kraan kan een massa van $6$ ton dus nog hangen?

Zo'n massa kan maximaal $20$ meter van het steunpunt van de draaiarm hangen.

Om een stapel stenen naar de goede plek te hijsen moet deze stapel $23$ m van het steunpunt van de draaiarm kunnen hangen. Welke massa mag die stapel stenen hoogstens hebben?

De massa mag maximaal $5217$ kg zijn.

$m=120000/a$ geeft $m=120000/23≈5217$ .

De massa mag maximaal $5217$ kg zijn.

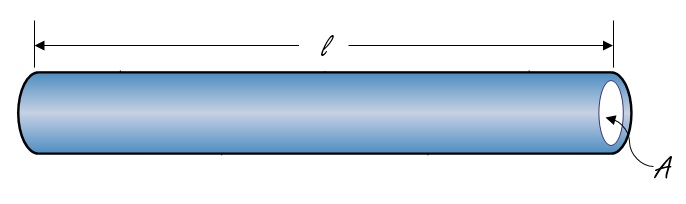
De weerstand die een elektrische stroom ondervindt in een koperdraad bereken je met de volgende formule:
$R=rho*l/A$

Hierin is:

$R$ de weerstand in ohm (Ω)

$rho$ de soortelijke weerstand van het materiaal in ohm meter (Ωm)

$l$ de lengte in meter (m)

$A$ de doorsnede in vierkante meter (m2)

De soortelijke weerstand van koper is $17*10^(text(-)8)$ Ωm.

Hoe groot moet de doorsnede van de koperdraad zijn om in $1$ m koperdraad een weerstand van meer dan $10$ Ω te krijgen?

Je moet oplossen $10 gt (17*10^(text(-)8))/A$ .
$(17*10^(text(-)8))/A = 10$ geeft $A = 17*10^(text(-)9)$ m2.
Grafiek: $A lt 17*10^(text(-)9)$ .

Welke diameter heeft zo'n koperdraad?

$A = pi r^2 = 17*10^(text(-)9)$ geeft $r ~~ 7,4 * 10^(text(-)5)$ m, dus dat zou een draad zijn met een diameter kleiner dan $0,074$ mm.

Los de volgende ongelijkheden op.

$8/m + 15 lt 20$

$m gt 1,6$

$8/m + 15$

$=$

$20$

$8/m$

$=$

$5$

$m$

$=$

$8/5 = 1,6$

Grafiek: $m gt 1,6$

$(11n)/4 + 25/7 ge 39/7$

$n ge 8/11$

$(11n)/4 + 25/7$

$=$

$39/7$

$(11n)/4$

$=$

$14/7$

$(11n)/4$

$=$

$2$

$11n$

$=$

$8$

$n$

$=$

$8/11$

$n ge 8/11$

$18/(x) gt 2x$

$x lt text(-)3$ en/of $0 lt x lt 3$

$18/(x)$

$=$

$2x$

$18$

$=$

$2x^2$

$x^2$

$=$

$9$

$x$

$=$

$3$ en/of $x = text(-)3$

Grafiek: $x lt text(-)3$ en/of $0 lt x lt 3$ .