de standaardafwijking van een verdeling uitrekenen en interpreteren;
een normale verdeling herkennen en typeren;
de vuistregels voor de normale verdeling gebruiken.
de belangrijkste principes van de beschrijvende statistiek;
de vorm van frequentieverdelingen (ook met klassenindelingen) te typeren;
met behulp van de mediaan en het gemiddelde de scheefheid van een verdeling benoemen.
|
som van de kwadraten |
||
Je hebt naar frequentieverdelingen leren kijken en centrummaten en spreidingsmaten leren gebruiken. Maar er is nog een belangrijke spreidingsmaat, namelijk de standaardafwijking.
Je ziet hier de resultaten van vergelijkbare metingen, verricht door verschillende studenten. De gemiddelden zijn aangegeven met en je ziet de standaardafwijkingen links en rechts van het gemiddelde.
De resultaten van student A zijn: , , , , , en .
De standaardafwijking van de resultaten van A bereken je zo (zie
Bereken eerst het gemiddelde.
Heb je een complete populatie dan is het gemiddelde .
Heb je een steekproef dan is het gemiddelde .
Bepaal van elk resultaat het verschil met het gemiddelde, de zogenaamde deviatie.
Kwadrateer elke deviatie (om geen negatieve afwijkingen te krijgen) en tel ze op.
Bereken de variantie.
Heb je een complete populatie dan is de variantie .
Heb je een steekproef dan is de variantie .
De standaardafwijking is de wortel uit de variantie.
Heb je een complete populatie dan is de standaardafwijking .
Heb je een steekproef dan is de standaardafwijking .
De resultaten van student A vormen een steekproef van alle mogelijke gelijke metingen en dus is de variantie en de standaardafwijking .
Je kunt de standaardafwijking ook met Excel berekenen, zie het practicum.
De standaardafwijking is de meestgebruikte spreidingsmaat bij statistisch onderzoek. Deze afwijking van het gemiddelde wordt links en rechts vanaf het gemiddelde uitgezet.
Bekijk de resultaten van de steekproeven van metingen door personen in Uitleg.
Bereken zelf de standaardafwijking van de resultaten van B.
Het gemiddelde is en .
Is de standaardafwijking een maat voor de precisie of voor de juistheid van de metingen?
De precisie.
Bij student A is het resultaat is nogal een uitschieter.
Hoe groot zijn het gemiddelde en de standaardafwijking van haar resultaten als je deze éne meting weglaat?
Het gemiddelde wordt dan en .
Stel je voor dat de resultaten van student C geen metingen zijn, maar alle resultaten voor zijn toetsen voor een bepaald vak in een bepaalde periode.
Hoe groot zijn het gemiddelde en de standaardafwijking in dat geval?
Nu is er geen sprake van een steekproef, dit is de populatie van zijn resultaten.
Het gemiddelde wordt dan en .
Van potten met augurken (uitlekgewicht gram) is geteld hoeveel augurken de potten bevatten. Van het resultaat zie je een tabel en een staafdiagram.
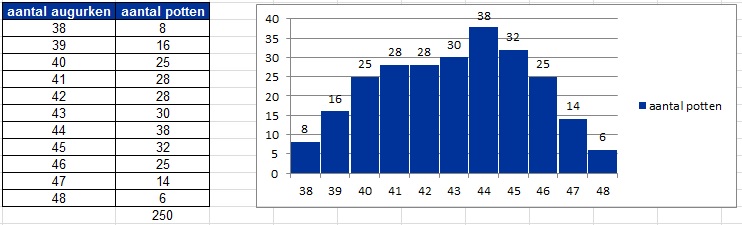
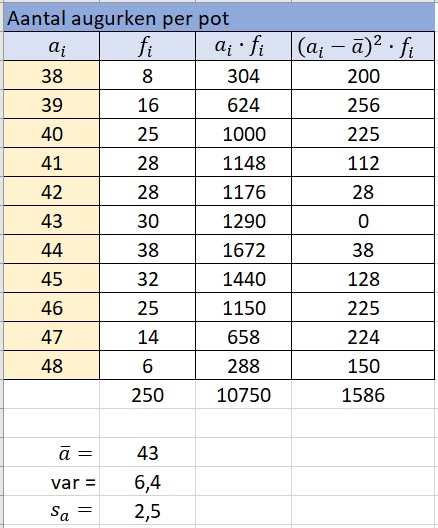
Om van deze steekproef het gemiddelde en de standaardafwijking te berekenen, moet je met de frequenties rekening houden.
Bereken van deze steekproef het gemiddelde en de standaardafwijking.
Zo kun je dit in Excel doen.
Je ziet een staafdiagram van de lengtes van een steekproef van vrouwen uit de dataset Statistiek Bijenkorf 1947. Er zijn relatieve frequenties gebruikt (in procenten). Daarom spreek je in dit geval wel van een histogram.
Dit histogram heeft een vrijwel zuivere
Beide getallen leggen de normale verdeling volledig vast, ze zijn karakteristiek voor deze normale verdeling.
Op grond van alleen het gemiddelde en de standaardafwijking kan elke normale verdeling worden getekend. En met die normale verdeling kun je gewoon berekenen hoeveel procent van de vrouwen een lengte van bijvoorbeeld meer dan cm hebben.
Vaak worden deze vuistregels voor de normale verdeling met gemiddelde en standaarddeviatie gebruikt:
Ongeveer % van alle waarden liggen tussen en .
Ongeveer % van alle waarden liggen tussen en .
Bijna% van alle waarden liggen tussen en .
Voor een steekproef zoals in de figuur gebruik je voor het gemiddelde en voor de standaardafwijking .
Bekijk Uitleg. Gebruik de dataset Statistiek Bijenkorf 1947 en het tabblad
Bereken zelf met behulp van Excel het gemiddelde en de standaardafwijking van deze steekproef.
Ga na, dat je dezelfde waarden vindt als in de Uitleg.
Gebruik waar nodig het practicum. Wees je er wel van bewust dat je met een frequentieverdeling te maken hebt.
Ga na dat bijna alle waarden binnen drie keer de standaarddeviatie van het gemiddelde afwijken.
en .
Er zijn ongeveer vrouwen kleiner dan en ongeveer vrouwen langer dan cm. Dat is in totaal % van de vrouwen die niet binnen drie keer de standaarddeviatie van het gemiddelde afwijken.
Controleer de vuistregel dat % van de vrouwen een lengte heeft tussen en .
en .
Daartussen zitten (tel % van de vrouwen in de klasse met midden en % van de vrouwen in de klasse met midden mee) ongeveer vrouwen en dat is % van de vrouwen.
Controleer de vuistregel dat % van de vrouwen een lengte heeft tussen en .
en .
Daartussen zitten (tel % van de vrouwen in de klasse met midden en % van de vrouwen in de klasse met midden mee) ongeveer vrouwen en dat is % van de vrouwen.
Men heeft ontdekt dat metingen van natuurlijke grootheden vaak normaal zijn verdeeld als je steekproef maar groot genoeg en aselect is.
De lengtes van vrouwen is daar een goed voorbeeld van, net al de lengtes van mannen, de vulgewichten van kilopakken suiker bij automatisch vullen, de gemeten pH-waarden in een vloeistoftank, etc.
Waarom moet hiervoor de steekproef groot genoeg zijn?
Bij een kleine steekproef kun je natuurlijk toevallig net veel lage waarden aantreffen.
Waarom zijn bijvoorbeeld de gewichten van mensen in een rijk land als Nederland waarschijnlijk niet normaal verdeeld?
Het gewicht kan door elk individu worden beïnvloed. In rijkere landen zie je vaak relatief veel mensen met overgewicht.
Waarom zullen lengtes van bijvoorbeeld basketballers niet normaal verdeeld zijn?
Daar zullen relatief veel lange mensen zijn.
Symmetrische frequentieverdelingen van een statistische variabele met een klokvorm zoals in de figuur, laten zich goed beschrijven door de
centrummaat
Die symmetrische verdeling noem je
In deze normale verdeling zie je het populatiegemiddelde en de bijbehorende standaardafwijking aangegeven.
Gaat het om een steekproef dan gebruik je het steekproefgemiddelde en de bijbehorende standaardafwijking .
Van een variabele met waarde en frequenties is de
(populatie) of (steekproef).
De standaardafwijking is de wortel uit de variantie:
(populatie) of (steekproef).
Elke normale verdeling wordt volledig bepaald door het gemiddelde en de standaardafwijking. De buigpunten van de normaalkromme zitten precies één standaardafwijking van de symmetrieas af. Voor elke normale verdeling gelden de vuistregels:
Ongeveer % van alle waarden liggen tussen en .
Ongeveer % van alle waarden liggen tussen en .
Bijna% van alle waarden liggen tussen en .
Je wilt de concentratie nitraat in landbouwgrond op een bepaald stuk land vaststellen.
Je neemt monsters, waarvan je hier de resultaten ziet.
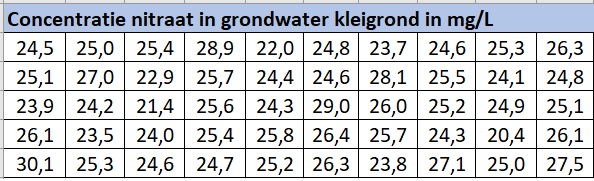
Bereken het gemiddelde en de standaarddeviatie van deze resultaten.
Maak bij deze gegevens ook een histogram met een klassenindeling , , ..., en zet er een bijpassende normale verdeling bij in.
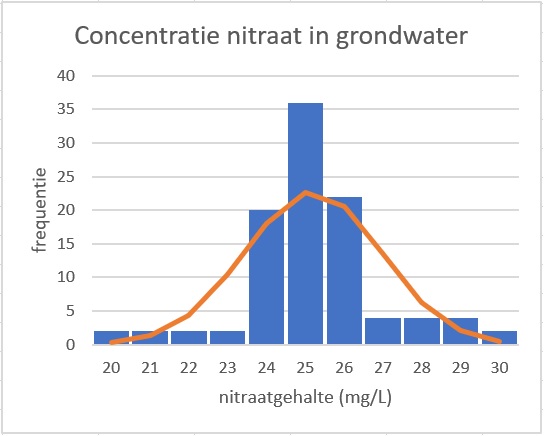
Je kunt dit gewoon met Excel doen met de ruwe data. Denk er dan wel om dat het om een steekproef gaat. Je gebruikt dus de functies STDEV() of STDEV.S(). Je vindt en .
Je maakt nu een combinatiediagram zoals dat hiernaast.
Maak eerst een frequentietabel met relatieve frequenties.
Teken daarvan een staafdiagram, dat is je histogram.
Maak vervolgens met Excel een tabel van de frequenties volgens de normale verdeling.
Maak van je histogram een combinatiediagram.
Bekijk
Voer zelf de berekeningen uit met behulp van Excel.
Hier zie je hoe dit er in Excel uitziet.
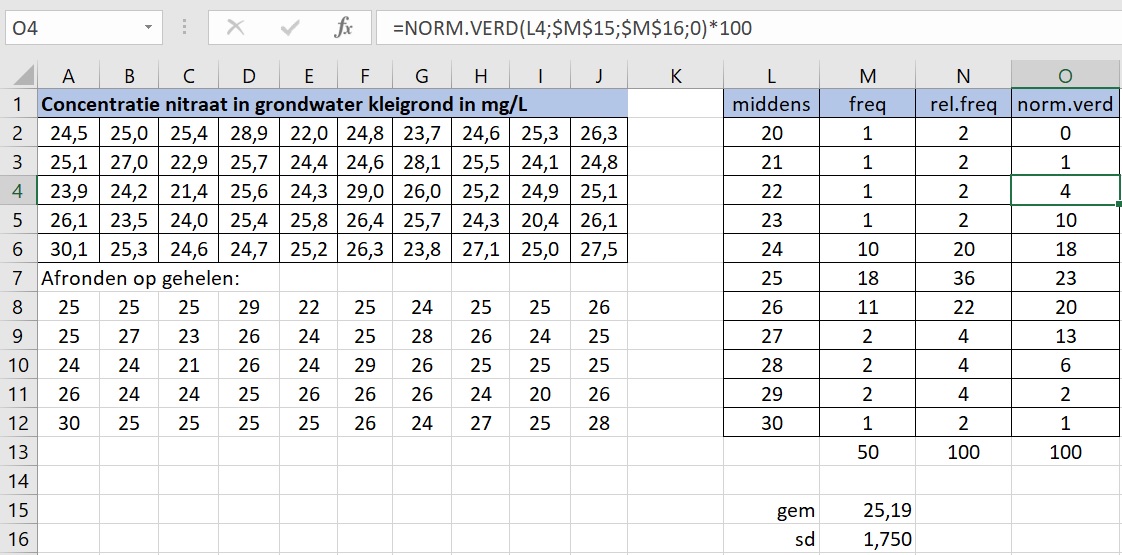
Je ziet dat de frequentieverdeling niet precies op een normale verdeling lijkt.
Ga of de % vuistregel klopt.
Volgens deze vuistregel moet % van de metingen tussen en liggen.
Nu is en .
Kijk je naar je frequentieverdeling, dan liggen daar van de metingen tussen en dat is %. Er zitten dus relatief veel metingen dicht bij het gemiddelde. De vuistregel klopt niet.
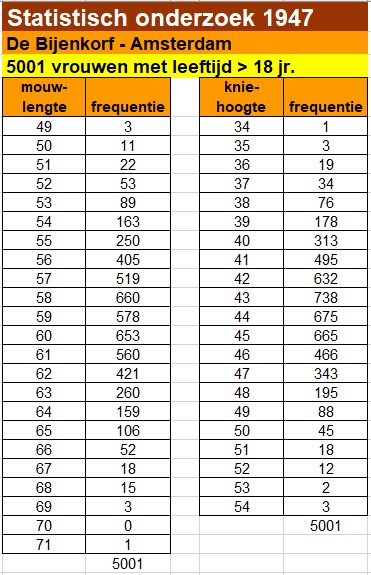
In 1947 hebben de wiskundigen Freudenthal en Sittig een grootscheeps onderzoek gehouden naar de lichaamsmaten van vrouwen in opdracht van De Bijenkorf. Daaruit wilde het bedrijf conclusies kunnen trekken betreffende de maatvoering van kleding voor hun vrouwelijke klanten.
Bereken het gemiddelde en de standaardafwijking van de mouwlengtes .
Onderzoek of deze frequentieverdeling voldoet aan de % vuistregel voor een normale verdeling.
Nu beschik je niet over de ruwe data, dus je kunt beide alleen schatten.
Het gemiddelde is .
Dus je maakt in Excel een kolom en die tel je op.
Delen door en je vindt .
De steekproefstandaardafwijking is .
Dus je maakt in Excel een kolom en die tel je op.
Delen door en worteltrekken je vindt .
Volgens de % vuistregel moet dat percentage van de metingen liggen tussen en .
Ga na, dat daar vrouwen tussen zitten. Bedenk dat je van de klasse met klassemidden de helft van het aantal moet nemen. En van de klasse met midden moet je keer het aantal nemen.
Het percentage is dan .
Dus deze frequentieverdeling voldoet redelijk goed aan de % vuistregel voor een normale verdeling.
Bekijk het berekenen van gemiddelde en standaardafwijking in het
Voer zelf deze berekeningen met behulp van Excel uit.
Gebruik het bestand dat je in het voorbeeld aantreft.
Controleer dat er inderdaad vrouwen tussen en zitten.
Het zijn er .
Controleer ook de % vuistregel.
Volgens de % vuistregel moet dat percentage van de metingen liggen tussen en .
Daar zitten vrouwen tussen. Van de klasse met klassemidden moet je keer het aantal nemen en van de klasse met midden moet je keer het aantal nemen.
Het percentage is dan .
Dus deze frequentieverdeling voldoet redelijk goed aan de % vuistregel voor een normale verdeling.
Acrylamide is een vermoedelijk kankerverwekkende stof die ontstaat in zetmeelrijke producten bij verhitting boven de °C. Voor gebakken frites is µg/kg de aanbevolen maximale hoeveelheid acrylamide. Een grote fastfoodketen laat onderzoeken of zijn frites aan dit referentieniveau voldoet. In een laboratorium worden daartoe porties frites van deze fastfoodketen onderzocht met de volgende resultaten.

Bereken het gemiddelde en de standaarddeviatie van deze metingen.
Gebruik Excel of werk met de hand en je rekenmachine.
Het gemiddelde is µg/kg en de standaarddeviatie is µg/kg.
Welke van deze twee waarden zegt iets over de precisie van de metingen?
De standaardafwijking.
Deze steekproef is klein, dus een normale verdeling zal er wel niet in zitten.
Controleer de % vuistregel en de % vuistregel.
en .
Daar zitten waarden tussen en dat is %.
De % vuistregel klopt niet.
en .
Daar zitten waarden tussen en dat is %.
De % vuistregel klopt ongeveer.

In 1947 hebben de wiskundigen Freudenthal en Sittig een grootscheeps onderzoek gehouden naar de lichaamsmaten van vrouwen in opdracht van De Bijenkorf. Daaruit wilde het bedrijf conclusies kunnen trekken betreffende de maatvoering van kleding voor hun vrouwelijke klanten.
Bekijk de frequentieverdeling van de kniehoogtes.
Bereken hiervan het gemiddelde en de standaardafwijking.
Werk met het Excelbestand.
Het gemiddelde is en de standaardafwijking is cm.
Maak van deze frequentieverdeling een histogram en zet daar de bijpassende normale verdeling bij in.
Zie figuur.
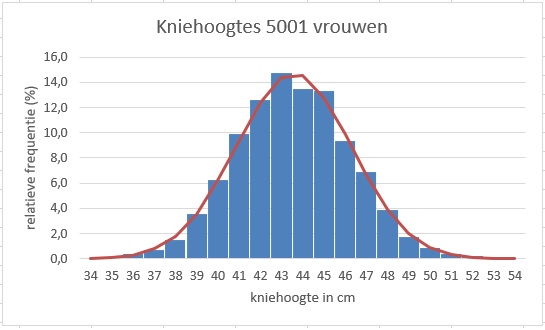
Ga na, of deze frequentieverdeling aan de % vuistregel voldoet.
en .
Daar zitten waarden tussen en dat is %.
De % vuistregel klopt.
Uit de wielersport komen regelmatig berichten over dopinggebruik. Wielrenners lijken
naar verboden middelen te grijpen om hun prestaties te verhogen. Een van de meest
genoemde stoffen is erytropoëtine, kortweg EPO. Dit middel bevordert de aanmaak van
rode bloedlichaampjes, waardoor de zuurstoftransportfunctie van het bloed wordt
vergroot. Je gaat hierdoor beter presteren.
De hematocrietwaarde is de
hoeveelheid rode bloedlichaampjes als percentage van de totale hoeveelheid bloed.
Die hematocrietwaarde stijgt als een wielrenner EPO gaat gebruiken.
Bij een
wielerwedstrijd in 1997 heeft men de hematocrietwaarde van een aantal wielrenners
gemeten. De meetresultaten staan in de tabel.
Bereken het gemiddelde en de standaardafwijking van de hematocrietwaarden van deze wielrenners.
Het gemiddelde is en de standaardafwijking is .
Waarom kan hier geen sprake zijn van een normale verdeling?
Deze frequentieverdeling is linksscheef.
De gemiddelde lengte van mannen is bij benadering normaal verdeeld. In 2010 was de gemiddelde lengte van de mannen in Nederland cm met een standaardafwijking van cm.
Schrijf de drie vuistregels op voor de lengte van mannen in 2010.
Ongeveer % van de mannen in Nederland heeft een lengte tussen cm en cm.
Ongeveer % van de mannen in Nederland heeft een lengte tussen cm en cm.
Bijna % van de mannen in Nederland heeft een lengte tussen cm en cm.
Schrijf nog minimaal uitspraken op over de lengte van mannen in 2010, gebaseerd op de vuistregels.
Bijvoorbeeld:
Ongeveer % van de mannen is langer dan cm.
Ongeveer % van de mannen is kleiner dan cm.
Ongeveer % van de mannen is langer dan cm en kleiner dan cm.
In waren mannen gemiddeld cm kleiner. De standaardafwijking was vrijwel hetzelfde, dus cm. Welke getallen in de antwoorden van de vorige twee vragen veranderen wel, en hoe, en welke niet?
De lengtes worden cm kleiner, de percentages veranderen niet.
De Unox stevige erwtensoep bevat volgens het etiket % rookworst. In een laboratorium wordt dit onderzocht. Deze waarden werden in monsters aangetroffen.
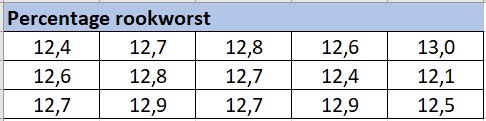
Bereken het gemiddelde percentage en de bijbehorende standaarddeviatie.
Gemiddelde %, standaardafwijking %.
Werk met Excel. Denk er om dat het hier om een steekproef gaat.
Gemiddelde %, standaardafwijking %.
Welke van beide maten zegt iets over de precisie van de metingen?
De standaarddeviatie.
Onderzoek of alle metingen minder dan drie standaarddeviaties afwijken van het gemiddelde.
Daar liggen alle waarden ruim binnen.
en .
Daar liggen alle waarden ruim binnen.
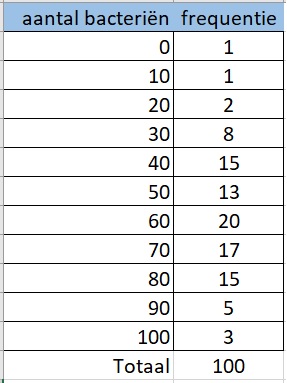
Een bedrijf haalt elke dag melk bij honderd boeren in de regio op. Voordat de melk in de transporttank gaat, wordt bij elke boer een monster van de melk genomen. In het lab wordt de melk onderzocht op het voorkomen van bacteriële vervuiling. Daartoe wordt in elk monster het aantal fecale bacteriën per centiliter geteld. De totale hoeveelheid melk die elke dag wordt opgehaald, heet een
De dienst die verantwoordelijk is voor de kwaliteitsbewaking, stelt als eis een maximum van fecale bacteriën per milliliter. In de tabel staan honderd waarden gegeven die het lab in een bepaalde dagproductie heeft gevonden.
Bereken een schatting van het gemiddelde en de standaardafwijking van deze gegevens.
Het gemiddelde bacteriën per centiliter.
De standaardafwijking .
Werk met Excel of maak met de hand extra kolommen voor en .
Het gemiddelde bacteriën per centiliter.
De standaardafwijking .
Onderzoek of deze frequentieverdeling bij benadering een normale verdeling is door de drie vuistregels te controleren.
Aan de % vuistregel wordt bijna voldaan en aan de % vuistregel ook, aan de % vuistregel wordt voldaan.
en .
Daar ligt % van de waarden binnen. Iets minder dan volgens de % vuistregel.
en .
Daar ligt % van de waarden binnen. Iets meer dan volgens de % vuistregel.
en .
Daar liggen alle waarden ruim binnen.
Aan de % vuistregel wordt bijna voldaan en aan de % vuistregel ook, aan de % vuistregel wordt voldaan.
De gemiddelde lengte van vrouwen is bij benadering normaal verdeeld. In was de gemiddelde lengte van de vrouwen in Nederland cm met een standaardafwijking van cm. Maak gebruik van de vuistregels en rond antwoorden af op halve procenten.
Hoeveel procent van de vrouwen was waarschijnlijk kleiner dan cm?
%
Pas de tweede vuistregel toe. Tussen en ligt naar schatting %; blijft nog % over, eerlijk verdelen, dus ongeveer % is kleiner dan .
Hoeveel procent van de vrouwen was waarschijnlijk kleiner dan cm?
%
Pas de tweede vuistregel toe. Tussen en ligt naar schatting %; blijft nog % over, eerlijk verdelen, dus ongeveer % is kleiner dan ; en dus kleiner dan is ongeveer %.
Hoe groot is de kans dat een willekeurige vrouw groter is dan cm?
%
Pas de tweede vuistregel toe. Tussen en ligt naar schatting %; blijft nog % over, eerlijk verdelen, dus ongeveer % is groter dan .
Van gegevens die in Excel beschikbaar zijn kun je diagrammen maken en centrum- en spreidingsmaten berekenen, zie Statistiek: Data presenteren.
Voor uitschieters kun je Dixon's Q-test toepassen.