een percentage onder een normale verdeling berekenen;

het gemiddelde of de standaardafwijking van een normale kansverdeling te berekenen.

de standaardafwijking van een frequentieverdeling uitrekenen en interpreteren;

een normale verdeling herkennen en typeren;

de vuistregels voor de normale verdeling gebruiken.

Statistische variabelen zoals het gewicht van appels, de lengte van een grote groep mensen, vulgewichten van literpakken, en dergelijke zijn vaak normaal verdeeld. Bijvoorbeeld is de lengte $L$ (in cm) van de populatie volwassen Nederlandse mannen een normale statistische variabele.
Je ziet hier dat de gemiddelde lengte $mu_L = 182$ cm is met een standaarddeviatie van $sigma_L = 7$ cm. Je kunt dan het percentage mannen dat kleiner dan $180$ cm is berekenen met bijvoorbeeld Excel, zie het Practicum.
De uitkomst van de normale verdeling noteer je als: $text(P)(L lt 180) ~~ 0,387$ .
Dit levert op: $0,387*100 = 38,7$ %.

Belangrijk is wel om je te realiseren dat de meetnauwkeurigheid hier een rol speelt.
De normale verdeling houdt met de nauwkeurigheid van het meten geen rekening, maar in de praktijk moet je daar wel rekening mee houden. Als je van iemand zegt dat hij $180$ cm lang is, dan heeft hij een lengte van $179,5 - lt 180,5$ cm. Dus is het deel van de mannen dat kleiner is dan $180$ cm eigenlijk $text(P)(L lt 179,5) ~~ 0,360$ .

Bekijk de verdeling van de lengtes van Nederlandse mannen in Uitleg.

Waarom worden hier $mu_L$ en $sigma_L$ gebruikt en niet $bar(L)$ en $s_L$ ?

Omdat dit gegevens zijn van de hele populatie Nederlandse mannen.

Ga zelf na, dat $text(P)(L lt 180) ~~ 0,387$ . Bekijk indien nodig het Practicum.

Voer in Excel in: =NORM.VERD(180;182;7;1).

Bij de lengtes van de mannen is afgerond op gehele cm. Het getal $180$ is dus een klassenmidden.

Van welke klasse?

De klasse $179,5 - lt 180,5$ .

Je wilt weten hoeveel procent van de mannen kleiner of gelijk aan $180$ cm is.
Je houdt ook met de meetnauwkeurigheid rekening.

Bereken dit percentage.

$text(P)(L lt 180,5) ~~ 0,415$ , dus $41,5$ %.

Bereken hoeveel procent van de mannen tussen $175$ en $189$ cm lang is.
Houd rekening met de meetnauwkeurigheid.

$text(P)(L lt 189,5) - text(P)(L lt 174,5) ~~ 0,716$ , dus $71,6$ %.

Ga na, dat de $68$ % vuistregel klopt.

Die vuistregel zegt dat $68$ % van de mannen tussen $175$ en $189$ moet zitten. Hierbij houd je met de meetnauwkeurigheid geen rekening.
$text(P)(L lt 189) - text(P)(L lt 175) ~~ 0,683$ , dus $68,3$ %.

Ga weer uit van de verdeling van de lengtes van Nederlandse mannen in Uitleg.

Waarom is $text(P)(L = 180) = 0$ als je niet met de meetnauwkeurigheid rekening houdt?

Omdat je nooit een man kunt vinden die precies $180,0000000...$ cm lang is.
Met de normale verdeling zou je ook $text(P)(L lt 180) - text(P)(L lt 180) = 0$ krijgen.

Bereken $text(P)(L = 180)$ als je wel met de meetnauwkeurigheid rekening houdt.
Hoeveel procent van de mannen is dus $180$ cm?

$text(P)(L lt 180) - text(P)(L lt 180) ~~ 0,055$ en dat is $5,5$ %.

Als je wilt berekenen hoeveel procent van de mannen groter is dan $180$ cm, dan gebruik je dat onder de normale verdeling $100$ % van de mannen valt.

Bereken hoeveel procent van de mannen langer is dan $180$ cm. Houd rekening met de meetnauwkeurigheid.

$1 - text(P)(L lt 180,5) ~~ 0,585$ , dus $58,5$ %.

Je ziet hier dat de gemiddelde lengte van mannen $mu_L = 182$ cm is met een standaarddeviatie van $sigma_L = 7$ cm. Je kunt dan het percentage mannen dat kleiner dan $180$ cm is berekenen met behulp van de z-tabel

Alle normale verdelingen zijn door verschuiven met $mu$ en vermenigvuldigen met $1/(sigma)$ in de $x$ -richting te vervormen naar de standaardnormale verdeling met $mu=0$ en $sigma=1$ . De waarden van die standaardnormale verdeling heten $z$ -waarden.

Hier geldt dus $z = (L - mu_L)/(sigma_L) = (L - 182)/7$ .

En dus is:

$text(P)(L lt 180) = text(P)(z lt (180 - 182)/7) = text(P)(z lt text(-)0,29) ~~ 0,3859$ .

In de standaardnormale tabel, of z-tabel, kun je nu de uitkomst aflezen, zie figuur.

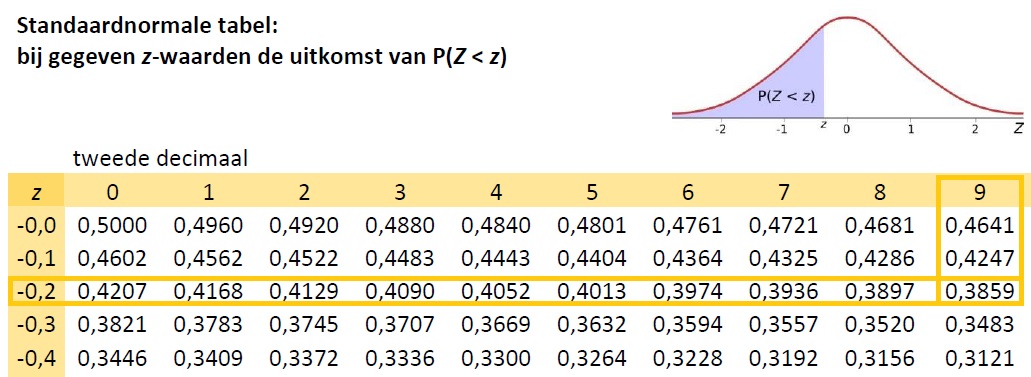
Je zult zien dat het werken met deze standaardnormale tabel zijn voordelen heeft.

Bekijk de Uitleg. Gebruik de tabel met $z$ -waarden.

Bereken $text(P)(L lt 179,5)$ .

$text(P)(L lt 179,5) = text(P)(z lt (179,5-182)/7) = text(P)(z lt text(-)0,36) ~~ 0,3594$ .

Hoeveel procent van de mannen heeft een lengte van $180$ cm als je met de meetnauwkeurigheid rekening houdt?

$text(P)(L lt 180,5) - text(P)(L lt 179,5) = text(P)(z lt text(-)0,21) - text(P)(z lt text(-)0,36) ~~ 0,4168 - 0,3594$ $=$ $0,0574$ en dat is $5,7$ %. (De afrondingen van de $z$ waarden zorgen voor kleine afwijkingen.)

Bereken hoeveel procent van de mannen langer is dan $180$ cm. Houd rekening met de meetnauwkeurigheid.

$1 - text(P)(L lt 180,5) = 1 - text(P)(z lt text(-)0,21) ~~ 1 - 0,4168 = 0,5832$ , dus $58,3$ %.

Statistische variabelen zoals het gewicht van appels, de lengte van een grote groep mensen, vulgewichten van literpakken, en dergelijke zijn vaak normaal verdeeld. Je spreekt dan van een normale statistische variabele.

De wiskundige Gauss (1777-1855) vond een formule voor de grafiek van de bijpassende normaalkromme of gausskromme. In bijvoorbeeld Excel, maar ook in GeoGebra of een rekenmachine is de formule voor die normaalkromme geprogrammeerd. Daarmee kun je relatieve frequenties bij de normale verdeling berekenen, zie het Practicum.

De relatieve frequentie die wordt weergegeven door de gekleurde oppervlakte noteer je als:

$text(P)(165 ≤ L < 180)$

Omdat $text(P)(L=165) = 0$ is dit hetzelfde als $text(P)(165 < L < 180)$ .

Als je wilt berekenen wat de relatieve frequentie is dat iemand afgerond een lengte heeft van 165 centimeter, dan moet je $text(P)(164,5 < X < 165,5)$ berekenen.

Hanteer de afspraak dat je bij een normale verdeling geen rekening houdt met afrondingen, tenzij duidelijk in de vraagstelling naar voren komt dat dit moet.

Alle normale verdelingen zijn om te zetten naar de standaardnormale verdeling. De waarden hiervan zijn de $z$ -waarden:

$z=(x-mu_X)/(sigma_X)$

Met de standaardnormale tabel kun je de bijbehorende relatieve frequenties bepalen.

De lengte $L$ van de Nederlandse mannen is normaal verdeeld met een gemiddelde van $μ=182$ centimeter en een standaardafwijking van $σ=7$ centimeter.

Bereken $text(Ρ)(170 < L < 180 )$ , $text(Ρ)(L < 180 )$ , $text(Ρ)(L=180 )$ .

Bereken het percentage mannen dat langer is dan $1,75$ meter als je rekening houdt met de meetonnauwkeurigheid.

Al deze kansen zijn met Excel te vinden. Maar je kunt ook GeoGebra gebruiken, of een rekenmachine. En je kunt werken met de standaardnormale tabel.
Bekijk het Practicum.

$text(P) (170 < L < 180 )≈0,3443$

$text(P) (L < 180 )≈0,3875$

$text(P) (L=180 )=0$

Bereken het percentage mannen dat langer is dan $1,75$ meter kun je vertalen naar:
$text(P)(L > 175,5) ~~ 0,8234$ . Dat is gelijk aan ongeveer $82,3$ %.

Gebruik de gegevens uit Voorbeeld.

Wat betekent $text(P)(162 < L < 178 )$ in dit verband?

De kans dat een willekeurige man een lengte heeft tussen $162$ en $178$ cm als je geen rekening houdt met de meetnauwkeurigheid.

Hoeveel procent van de mannen heeft een lengte tussen $171$ en $178$ centimeter?

Er staat niet dat je rekening met de meetnauwkeurigheid moet houden, dus dat doe je ook niet.

$text(P)(171 < L < 178\|\mu = 182 text( en ) sigma = 7)≈0,226$ , dus ongeveer $22,6$ %.

Hoeveel procent van de mannen heeft een lengte van precies $171$ centimeter?

$0$ %.

Hoeveel procent van de mannen heeft een lengte van $171$ centimeter als je met de meetnauwkeurigheid rekening houdt?

$text(P)(170,5 < L < 171,5)≈0,017$ , dus ongeveer $1,7$ %.

Hoeveel procent van de soldaten van deze kazerne heeft een lengte vanaf $μ-1,5 *σ$ tot $μ+1,5 *σ$ ?

86,6%

$μ-1,5 *σ = 182 - 10,5 = 171,5$ en $μ+1,5 *σ = 182 + 10,5 = 192,5$

$text(P)(171,5 ≤L < 192,5 )≈0,866$ , dus ongeveer $86,6$ %.

Het gewicht $G$ van een bepaalde appelsoort is normaal verdeeld met een gemiddelde van $150$ gram en een standaardafwijking van $17$ gram.

Hoeveel procent van deze appels weegt minder dan $140$ gram?

$text(P)(G < 140)≈0,278$ , dus $27,8$ %.

Hoeveel procent van deze appels heeft een gewicht dat minder dan $10$ gram afwijkt van het gemiddelde?

44,4%

$text(P)(140 < L < 160\|\μ=150 text( en ) σ=17 )≈0,444$
Het percentage is $44,4$ %.

Een groenteboer heeft nog $340$ van deze appels.

Hoeveel daarvan zijn lichter dan $120$ gram?

$text(P)(G < 120)≈0,039$

$0,039 *340 ≈13$ appels.

Er wordt gewerkt met een meetnauwkeurigheid van $1$ gram.

Maakt dit verschil voor je antwoord bij c?

$text(P)(G < 119,5)≈0,036$

$0,036 *340 ≈12$ appels, dus ja, het maakt verschil.

De lengte $L$ van een een grote steekproef Nederlandse mannen is normaal verdeeld met een gemiddelde van $bar(L)=182$ cm en een standaardafwijking van $s_L=7$ cm.

Welke lengtes hebben de $20$ % langste mannen in deze steekproef?

Vertaal deze vraag in: bereken grenswaarde $g$ als $text(Ρ)(L>g)=0,20$ .

Excel, GeoGebra, een rekenmachine hebben hiervoor een speciale functie. Die stelt je in staat om vanuit een gegeven kans de grenswaarde terug te vinden. Je kunt ook werken met $z$ -waarden. Alleen moet je omrekenen naar kleiner-of-gelijk-frequenties.

$text(Ρ)(L>g)=0,20$ betekent dat $text(Ρ)(L < g)=1 - 0,20 = 0,80$ .
Dus $text(P)(z lt (g-183)/7) = 0,80$ .
In de standaardnormale tabel vind je zo dicht mogelijk bij $0,8000$ een $z$ -waarde, namelijk $z~~0,84$ .
Dus: $(g-183)/7 ~~ 0,84$

De uitkomst is: $g ~~ 0,84*7 + 183 = 187,9$ .
De $20$ % langste mannen zijn $187,9$ cm of langer.

Gebruik de gegevens uit Voorbeeld.

Welke lengtes hebben de $20$ % kleinste mannen in deze groep?

$text(P)(L≤g) = text(P)(z le (g-182)/7)=0,20$ en hieruit volgt $(g-182)/7~~text(-)0,84$ en $g~~text(-)0,84*7+182≈176,1$ cm.

Bedenk dat je dit ook zonder z-tabel kunt berekenen, want deze grenswaarde ligt even ver van de gemiddelde lengte van $182$ cm af als lengte van $187,9$ cm (vanwege symmetrie) die de grenswaarde was voor de $20$ % langste mannen.

$10$ % van de mannen zit boven het gemiddelde, maar is toch niet langer dan $a$ centimeter. Bereken $a$ .

$text(P)(L≤a) = text(P)(z le (a-182)/7)=0,60$ en hieruit volgt $(a-182)/7~~0,25$ en $g~~0,25*7+182≈183,8$ cm.

De steekproef bestond uit $1200$ mannen.
Voor deze groep mannen worden T-shirts aangeschaft in drie maten: S (small), M (medium) en L (large). Deze maten worden zo gemaakt dat elke maat precies voor $1/3$ deel van de mannen geschikt is.

Voor welke lengtes is maat S geschikt?
Houd rekening met de meetnauwkeurigheid.

Uit $text(P)(L≤g)=1/3$ volgt $g≈179,0$ cm. De maat small is geschikt voor mannen die maximaal $178$ cm lang zijn.

Voor welke lengtes is maat M geschikt?

Door het antwoord bij c is bekend dat het hier in ieder geval om mannen gaat met een lengte vanaf $179$ cm.

$text(P)(L≤g)=2/3$ geeft $g≈185,0$ cm. De maat M is voor mannen met een lengte vanaf $179$ cm en tot en met $184$ cm.

In een suikerfabriek is het vulgewicht van kilopakken suiker ingesteld op een gemiddelde van $μ=1002$ gram en een standaardafwijking van $σ=3$ gram. Maar nu bevat ongeveer $25$ % van de pakken minder dan $1000$ gram.
De fabrikant wil dat niet meer dan $5$ % van de pakken minder dan $1000$ gram bevat.
Hij kan dit bijvoorbeeld bewerkstelligen door het gemiddelde vulgewicht $μ$ te verhogen, maar dat is een te dure oplossing.
De fabrikant kan dit ook voor elkaar krijgen door de vulmachine nauwkeuriger te laten werken: hij verkleint de standaardafwijking $σ$ .

Met de applet kun je de aangepaste waarde van $σ$ vinden, maar hoe bereken je die?

$G$ is het gewicht van een pak suiker uit de suikerfabriek.

Nu moet $text(P)(G < 1000) = 0,05$ , dus $text(P)(z lt (1000-1002)/(sigma)) = 0,05$ .

De $z$ -waarde bij $0,05$ haal je uit de standaardnormale tabel: $z=text(-)1,645$ .

$(1000-1002)/(sigma) = text(-)1,645$ geeft $sigma = (text(-)2)/(text(-)1,645)~~1,22$ .

De standaardafwijking moet afnemen van $3$ gram naar $1,22$ gram om aan de nieuwe eis te kunnen voldoen.

Gebruik de gegevens van de suikerfabriek in Voorbeeld.

Waarom is het verhogen van het gemiddelde voor de fabrikant een dure oplossing?

De fabrikant moet dan gemiddeld méér suiker in een pak stoppen.

Bereken wat het vulgewicht zou moeten worden om aan de eis te voldoen.
Nu blijft dus de standaarddeviatie hetzelfde.

$text(P)(G ≤ 1000) = text(P)(z le (1000-mu)/3)=0,05$ en hieruit volgt $(1000-mu)/3~~text(-)1,64$ en $mu~~1000 + 3*1,64≈1004,9$ gram.

Welke mogelijke voor- en nadelen heeft het verkleinen van de standaarddeviatie voor de fabrikant?

Het voordeel voor de fabrikant is dat dit ongeveer evenveel suiker kost, het nadeel kan zijn dat hij een nieuwe machine moet aanschaffen die nauwkeuriger is.

De eisen worden aangescherpt: niet meer dan $2,5$ % van de pakken suiker mag minder dan $1000$ gram wegen.

Welke standaarddeviatie moet de fabrikant dan hanteren als hij het gemiddelde gewicht gelijk van zijn pakken suiker houdt?

Nu moet $text(P)(G < 1000) = 0,025$ , dus $text(P)(z lt (1000-1002)/(sigma)) = 0,025$ .

De $z$ -waarde bij $0,025$ haal je uit de standaardnormale tabel: $z=text(-)1,96$ .

$(1000-1002)/(sigma) = text(-)1,96$ geeft $sigma = (text(-)2)/(text(-)1,96)~~1,02$ .

Is het mogelijk om te eisen dat $0$ % van de pakken te licht is? Licht je antwoord toe.

Nee, het vulgewicht van een pak suiker is een toevalsvariabele, dus er blijft altijd een (heel kleine) mogelijkheid dat er pakken te licht zijn.

Van een bepaald type batterij is de levensduur normaal verdeeld met een gemiddelde van $80$ uur en een standaardafwijking van $255$ minuten.

De fabrikant vermeldt op de verpakking dat deze batterijen $75$ uur meegaan. Hoeveel procent van de batterijen haalt deze levensduur niet?

$sigma = 255$ minuten en dit is gelijk aan $255/60 = 4,25$ uur.

$P(L < 75)≈0,120$ en hieruit volgt dat het percentage $12,0$ % is.

Door het verbeteren van het fabricageproces gaan de batterijen gemiddeld langer mee. De standaardafwijking van de levensduur blijft hetzelfde. De fabrikant garandeert nu dat slechts $1$ % van de batterijen geen $90$ uur meegaat. Hoe groot is nu de gemiddelde levensduur van dit soort batterijen?

$text(P)(L < 90) = text(P)(z lt (90-mu)/(4,25))=0,01$

Met de z-tabel vind je $μ≈99,9$ uur en dat is ongeveer $100$ uur.

Een vulmachine vult kilopakken rijst. Het ingestelde vulgewicht van de machine komt overeen met het gemiddelde gewicht van de pakken rijst. De gewichten zijn normaal verdeeld. Het gemiddelde gewicht van een pak rijst is $1010$ gram en de standaardafwijking is $9$ gram.

Hoeveel procent van de pakken weegt minder dan $1000$ gram?

$text(P)(G < 1000) ~~ 0,133$ , dus $13,3$ %.

Hoeveel procent van de pakken weegt meer dan $1000$ gram?

$text(P)(G > 1000) = 1 - text(P)(G < 1000) ~~ 0,867$ , dus $86,7$ %.

Hoeveel procent van de pakken is meer dan $5$ gram zwaarder dan het gemiddelde?

$text(P)(G > 1005) = 1 - text(P)(G lt 1005) ~~ 0,7107$ , dus $71,1$ %.

Hoeveel procent van de pakken weegt tussen de $1005$ en de $1015$ gram?

$text(P)(1005 < G < 1015) = text(P)(G lt 1015) - text(P)(G lt 1005) ~~ 0,4215$ , dus $42,2$ %.

Je ziet hier de relatieve frequentieverdeling van de lengtes van een steekproef van $5001$ vrouwen in 1947.

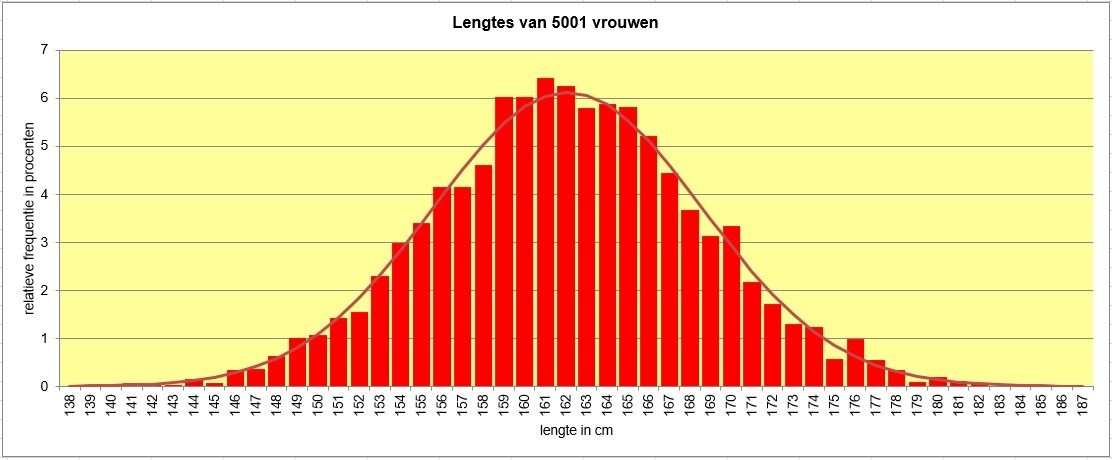
Bij dit histogram past een normaalkromme met gemiddelde $bar(L)~~162,1$ en een standaardafwijking $s_L ~~ 6,5$ .

Houd er rekening mee dat alle lengtes op gehele cm zijn afgerond.

Hoeveel procent van deze vrouwen was langer dan $170$ cm?

$text(P)(L gt 170,5) = 1 - text(P)(L lt 170,5) ~~ 0,0981$ dus $~~9,8$ %.

Hoeveel procent van deze vrouwen had een lengte tussen $160$ en $170$ cm?

$text(P)(160,5 lt L lt 169,5) = text(P)(L lt 169,5) - text(P)(L lt 160,5) ~~ 0,4698$ dus $~~47,0$ %.

Hoeveel procent van deze vrouwen had een lengte van $160$ cm lang?

$text(P)(159,5 lt L lt 160,5) = text(P)(L lt 160,5) - text(P)(L lt 159,5) ~~ 0,0582$ dus $~~5,8$ %.

Hoe lang waren de $10$ % kleinste vrouwen?

$text(P)(L lt g) ~~ 0,10$ betekent $text(P)(z lt (g-162,1)/(6,5)) ~~ 0,10$ .
De z-tabel geeft $(g-162,1)/(6,5) ~~ text(-)1,28$ , dus maximaal $g ~~ 153,78$ cm.
Die vrouwen waren maximaal $153$ cm lang.

En hoe lang waren de $10$ % langste vrouwen?

Minimaal $170,3$ , dus minimaal $171$ cm.

Een bakker bakt kerststollen van $1000$ gram.

Er wordt een grote steekproef van deze kerststollen onderzocht. Het gemiddelde gewicht hiervan bedraagt $bar(G) = 1000$ g. Echter $5$ % van de stollen in deze steekproef weegt minder dan $900$ gram.

Hoeveel bedraagt de standaardafwijking van deze steekproef?

Los op met de standaardnormale tabel: $text(P)(G lt 900) = text(P)(z lt (900-1000)/(s_G)) = 0,05$

Dit geeft: $s_G ~~ 60,8$ gram.

Als de standaardafwijking van de stollen in werkelijkheid $60$ gram is, hoeveel procent van de stollen weegt dan minder dan $900$ gram?

$100 * text(P)(G < 900) ~~ 4,8$ %.

Hoeveel bedraagt het gewicht van de $3$ % zwaarste kerststollen als het gemiddelde $1000$ gram is met een standaardafwijking van $60$ gram?

$text(P)(G lt g) ~~ 0,97$ geeft $text(P)(z lt (g-1000)/(60)) ~~ 0,97$ .
Dus $(g-1000)/(60) ~~ 1,88$ en $g ~~ 1112,8$ g.
Deze zwaarste kerststollen zijn $1113$ gram of zwaarder.

In het Moeders voor moeders babyboek staat dat $75$ % van de zwangere vrouwen bevalt tussen $14$ dagen vóór en $14$ dagen na de uitgerekende datum. Bij het bepalen van deze uitgerekende datum gaat men uit van een zwangerschap van $40$ weken. De zwangerschapsduur is bij benadering normaal verdeeld met een gemiddelde van $280$ dagen.

Bereken de bijbehorende standaardafwijking in één decimaal nauwkeurig.

$75$ % van de zwangerschappen duurt tussen $280 - 14 = 266$ en $280 + 14 = 294$ dagen.

Dus $12,5$ % van de zwangerschappen duurt minder dan $266$ dagen.

$text(P)(T lt 266) = text(P)(z lt (266-280)/(sigma)) = 0,125$ .

Dit geeft: $σ ≈ 12,2$ dagen.

In 2002 vonden er in Nederland $199205$ bevallingen plaats. Van een aantal van deze bevallingen duurde de zwangerschap minder dan $36$ weken.

Bereken bij hoeveel bevallingen dit het geval was.

Bij ongeveer $199205 * text(P)( T < 252) ~~ 2164$ bevallingen duurde de zwangerschap minder dan $36$ weken.

De accu van een tablet van het merk S gaat gemiddeld $2,60$ jaar mee met een standaardafwijking van $0,32$ jaar. De tableteigenaars zijn hiermee niet tevreden en daarom wil S de productiestraat van deze accu’s aanpassen.
Er zijn aanpassingen mogelijk die de gemiddelde levensduur zullen verhogen: per extra levensweek zijn de kosten hiervan € 0,01 per tablet.
Andere aanpassingen zorgen voor een kleinere standaardafwijking, maar deze aanpassingen kosten per extra levensweek € 0,02 per tablet.

S wil de productiestraat zodanig aanpassen dat de kans dat de accu meer dan twee jaar meegaat minstens $97,5$ % wordt. Echter: de totale extra kosten per tablet door de aanpassingen mogen niet hoger zijn dan $1,4$ eurocent.

Onderzoek of er mogelijkheden zijn voor S om de productiestraat zodanig aan te passen dat aan beide voorwaarden wordt voldaan.

De normaal verdeelde kansvariabele $L$ is het aantal jaren levensduur van een tablet van merk S.

Alleen het gemiddelde aanpassen, zodanig dat $text(P)(L>2) >= 0,975$ :

$text(P)(L gt 2) = text(P)(z lt (2-mu)/(0,32)) = 0,975$ geeft een gemiddelde van $2,62$ levensjaar: $0,027$ levensjaar extra.

de kosten hiervan zijn $(0,027 * 52) * 0,01 = 0,01404$ euro en dat is meer dan $1,4$ eurocent per tablet: dit is te veel.

Alleen de standaardafwijking aanpassen, zodanig dat $text(P)(L>2) >= 0,975$ :

$P(L>2) = text(P)(z lt (2-2,60)/(sigma)) = 0,975$ geeft een standaardafwijking van $0,306$ levensjaar: $0,014$ levensjaar minder afwijking;

de kosten hiervan zijn $(0,014 * 52) * 0,02 = 0,01456$ euro en dat is meer dan $1,4$ eurocent per tablet: dit is te veel.

Een combinatie van aanpassingen aan gemiddelde en standaardafwijking is wellicht noodzakelijk:

Kies het gemiddelde weer iets kleiner dan de gevonden 2,627 (maar groter dan de oorspronkelijke 2,6) levensjaar,
en

Kies de standaardafwijking weer iets groter dan de gevonden 0,306 (maar kleiner dan de oorspronkelijke 0,32) levensjaar

totdat de kosten 1,4 eurocent per tablet of lager zijn.

Als het goed is, valt nu een patroon op: als je beide aanpast, komen de kosten nooit onder de $0,01456$ euro uit.

Het is daarom niet mogelijk om te sleutelen aan gemiddelde of standaardafwijking zodanig dat aan beide voorwaarden wordt voldaan.

Het vulvolume $V$ van een pak melk is normaal verdeeld met een gemiddelde van $1,02$ liter en een standaardafwijking van $0,015$ liter. De consument verwacht $1$ liter melk te kopen.

Hoeveel procent van de melkpakken bevat minder dan $1$ liter melk?

$~~9,12$ %.

$text(P)(V lt 1) ~~ 0,0912$ , dus $~~9,12$ %.

Hoeveel procent van de melkpakken bevat meer dan $1,03$ liter melk?

$~~25,25$ %.

$1-text(P)(V lt 1,03) ~~ 0,2525$ , dus $~~25,25$ %.

Je kunt niet bepalen hoeveel procent van de melkpakken een inhoud van precies $1$ liter heeft. Je kunt wel bepalen hoeveel procent van de melkpakken afgerond op twee decimalen $1$ liter bevat. Dan zie je dat het gaat om het gebied vanaf de grens $0,995$ tot de grens $1,005$ . En daar hoort wel degelijk een bepaald percentage bij.

Bereken dat percentage.

$~~11,09$ %

$text(P)(0,995 lt V lt 1,005) = text(P)(V lt 1,005) - text(P)(V lt 0,995) ~~ 0,1109$ , dus $~~11,09$ %

$5$ % van de melkpakken heeft een vulvolume van minder dan $g$ . Bereken $g$ .

$g~~0,9953$ liter.

$text(P)(V lt g) = text(P) (z lt (g-1,02)/(0,015)) = 0,05$ geeft $g~~0,9953$ liter.

Omdat iets minder dan $10$ % van de melkpakken te weinig melk bevat, besluit de fabrikant het gemiddelde vulgewicht te verhogen tot dit percentage minder dan $1$ % is.

Hoeveel moet daarvoor het gemiddelde vulgewicht worden?

$~~1,035$ liter.

$text(P)(V lt 1) = text(P) (z lt (1-mu)/(0,015)) = 0,01$ geeft $(1-mu)/(0,015) ~~ text(-)2,33$ en dus $mu ~~ 1,035$ L.

Bij een groep van $1000$ mannen is de bloeddruk normaal verdeeld met een gemiddelde van $bar(B) = 128,5$ mm Hg met een standaardafwijking van $s_B = 12,5$ mm Hg.

Hoeveel mannen hebben een bloeddruk die meer dan drie keer de standaardafwijking afwijkt van de gemiddelde bloeddruk?

Ongeveer $0,27$ %.

Hoeveel procent van de mannen heeft een bloeddruk van meer dan $150$ ?

Ongeveer $4,3$ %.

Hoeveel bedraagt de bloeddruk van de $10$ % mannen met de hoogste bloeddruk?

$144,5$ of meer.

Werken met de normale verdeling kun je via de standaardnormale tabel, of met Excel, maar ook met behulp van een rekenmachine of met GeoGebra.

Ga uit van een normaal verdeelde variabele $X$ met $mu_X = 100$ en $sigma_X = 5$ .

Werken met standaardnormale tabel:

$text(P)(X lt 96) = text(P)(z lt (96-100)/5) = text(P)(Z lt text(-)0,8) ~~ 0,2119$ , geeft $~~21,2$ %.

$text(P)(X gt 96) = 1 - text(P)(X lt 96) = 1 - text(P)(z lt (96-100)/5) = 1 - text(P)(Z lt text(-)0,8) ~~ 0,7881$ , geeft $~~78,8$ %.

$text(P)(96 lt X gt 107) = text(P)(X lt 107) - text(P)(X lt 96) = text(P)(z lt 1,2) - text(P)(z lt text(-)0,8) ~~ 0,6730$ , geeft $~~67,3$ %.

$text(P)(X lt g) = 0,05$ geeft $text(P)(z lt (g-100)/5) = 0,05$ en $(g-100)/5 ~~ text(-)1,645$ .
Dus $g ~~ 91,775$ .

Nieuwe $mu$ berekenen bij gegeven percentage:
$text(P)(X lt 90) = 0,05$ geeft $text(P)(z lt (90-mu)/5) = 0,05$ en $(90-mu)/5 ~~ text(-)1,645$ .
Dus $mu ~~ 98,225$ .

Nieuwe $sigma$ berekenen bij gegeven percentage:
$text(P)(X lt 90) = 0,05$ geeft $text(P)(z lt (90-100)/(sigma)) = 0,05$ en $(text(-)10)/(sigma) ~~ text(-)1,645$ .
Dus $sigma ~~ 6,08$ .

Werken met Excel:

$text(P)(X lt 96) ~~ 0,2119$ via =NORM.VERD(96;100;5;1).

$text(P)(X gt 96) = 1 - text(P)(X lt 96) ~~ 0,7881$ via =1-NORM.VERD(96;100;5;1).

$text(P)(96 lt X gt 107) = text(P)(X lt 107) - text(P)(X lt 96)~~ 0,6730$ via =NORM.VERD(107;100;5;1)-NORM.VERD(96;100;5;1).

$text(P)(X lt g) = 0,05$ geeft $g ~~ 91,775$ via =INV.NORM(0.05;100;5).

Nieuwe $mu$ berekenen bij gegeven percentage:
$text(P)(X lt 90) = 0,05$ geeft $text(P)(z lt (90-mu)/5) = 0,05$ en $(90-mu)/5 ~~ text(-)1,645$ via =INV.NORM(0.05;0;1).
Dus $mu ~~ 98,225$ .

Nieuwe $sigma$ berekenen bij gegeven percentage:
$text(P)(X lt 90) = 0,05$ geeft $text(P)(z lt (90-100)/(sigma)) = 0,05$ en $(text(-)10)/(sigma) ~~ text(-)1,645$ via =INV.NORM(0.05;0;1).
Dus $sigma ~~ 6,08$ .

Werken met GeoGebra:
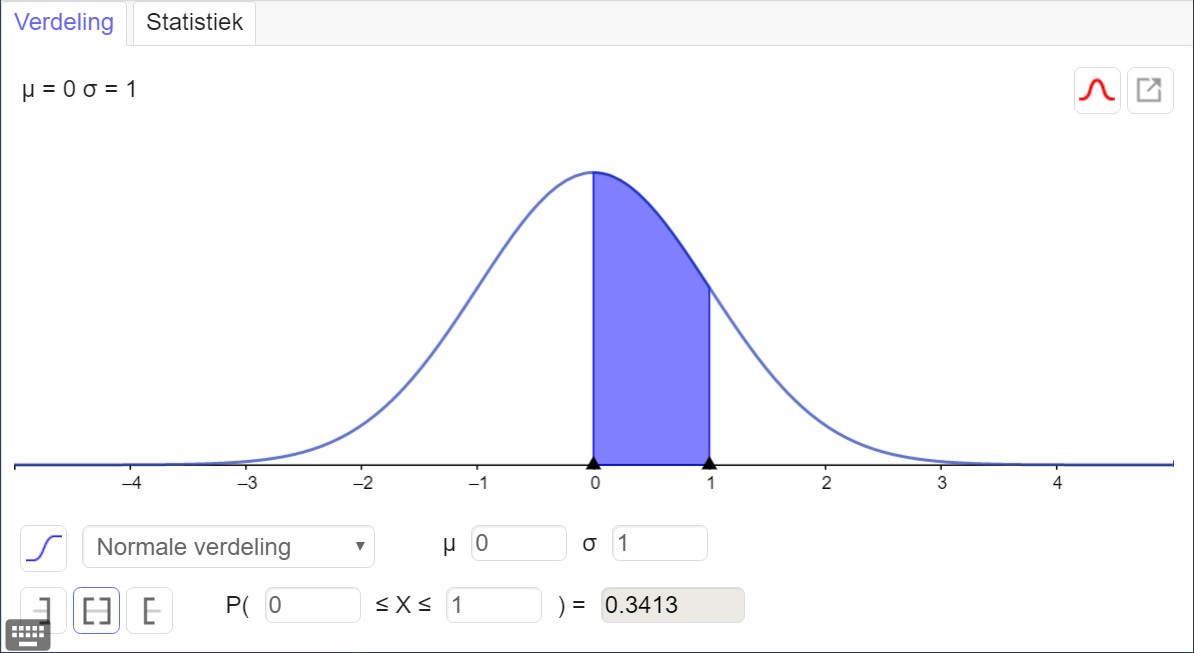
Gebruik de scherminstelling Kansrekening. Je ziet dan de normale verdeling en je kunt allerlei waarden gewoon instellen en aflezen.

Werken met de grafische rekenmachine TI-84:
Zie het practicum TI-84, Kansverdelingen en bekijk alles vanaf kanshistogrammen. Let wel: hier wordt vaak over kans gesproken in plaats van relatieve frequentie.