In dit onderwerp is het werken met verdelingen van vooral relatieve frequenties en dan met name de normale verdeling voorbij gekomen. Het gaat daarbij vooral om berekeningen met de normale verdeling, werken met betrouwbaarheidsintervallen en werken met controlekaarten.

Je hebt nu alle theorie van Normale verdeling doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan... Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je ermee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

symmetrische en niet-symmetrische frequentieverdelingen

standaardafwijking, standaarddeviatievariantienormaalkromme en zijn vuistregels

normale verdelingstandaardnormale tabel, $z$ -tabel $z$ -waarde

steekproevenverdelingbetrouwbaarheidsinterval

controlekaart, regelkaart, Shewhartkaart

beoordelen of een frequentieverdeling symmetrisch is of niet;

de standaarddeviatie van een frequentieverdeling berekenen en interpreteren is samenhang met de normaalkrommede vuistregels bij een normaalkromme toepassen;

een normale verdeling van relatieve frequenties karakteriseren door gemiddelde en standaarddeviatiebij een normale verdeling relatieve frequenties (percentages) berekenenbij gegeven percentages onder een normaalkromme gemiddelde of standaardafwijking berekenen;

de standaardafwijking van een steekproevenverdeling berekenen (de wortel-n-wet)een betrouwbaarheidsinterval voor metingen vaststellen;

werken met Shewhartkaarten.

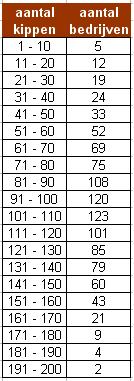
Uit onderzoek van het gemengde boerenbedrijf bleek het houden van kippen een belangrijke rol te spelen bij het tot stand komen van het inkomen van deze boeren. Daarom werd de boeren gevraagd het aantal kippen op hun bedrijf op te geven.

Waarom kun van deze gegevens het gemiddelde en de standaarddeviatie niet exact berekenen?

De gegevens zijn al verdeeld in klassen en je kunt de ruwe data niet meer zien.

Schat de centrummaten mediaan en gemiddelde. Onderbouw je schatting.

De mediaan is het gemiddelde van de 572e en 573e waarneming en valt in het midden van de klasse $101 - \le 110$ en is dus $~~105,5$ .

Voor de schatting van het gemiddelde werk je met de klassenmiddens:
$bar(K) = (5,5*5 + 15,5*12+ 25,5*19+ ....+ 185,5*4+195,5*2)/1044 ~~100,0$

Schat de standaardafwijking. Onderbouw je schatting.

Standaarddeviatie: $s_K ~~35,5$ .

De standaarddeviatie bereken je met Excel: afwijking ten opzichte van $100$ (gemiddelde) kwadrateren, vermenigvuldigen met frequentie, optellen, delen door $1044$ en wortel trekken.

Hoeveel procent van de bedrijven heeft meer dan $160$ kippen?

$(21+9+4+2)/1044* 100 ~~ 3,4$ %.

Hoeveel procent van de bedrijven heeft minder dan $41$ kippen?

$(5+12+19+24)/1044 * 100 ~~ 5,8$ %.

Hoe kun je de verdeling karakteriseren zonder er een diagram van te maken?

Redelijk symmetrisch met één top (in het midden), niet-scheef; benadert een normale verdeling.

Aan de frequentie in de tabel kun je zien dat de top rond $100-101$ kippen ligt en dat links en rechts in de frequentietabel min of meer getallen van gelijke grootte liggen. Er zijn misschien iets meer kleine ( $<=40$ ) dan grote bedrijven ( $>160$ ).

Je kunt de verdeling zo karakteriseren: redelijk symmetrisch met één top (in het midden), niet scheef, benadert een normale verdeling.

Bloeddruk wordt gemeten in mm Hg (spreek uit: millimeter kwikdruk).
Bij een groep van duizend Nederlandse mannen is de bloeddruk normaal verdeeld met een gemiddelde van $128,5$ mm Hg met een standaardafwijking van $12,5$ mm Hg.

Hoeveel procent van deze mannen hebben naar schatting een bloeddruk van minder dan $141$ mm Hg?

$bar(B)+s_B = 141$ . Maak gebruik van de vuistregels en de symmetrie van de normaalkromme. Dit geeft $84$ %.
Je kunt ook werken met de standaardnormale tabel: $text(P)(B lt 141) = text(P)(z lt (141-128,5)/(12,5)) = text(P)(z lt 1) ~~ 0,8413$ .

Hoeveel van deze mannen hebben naar schatting een bloeddruk die meer dan twee keer de standaardafwijking afwijkt van de gemiddelde bloeddruk?

Gebruik de tweede vuistregel van de normaalkromme. Dit geeft ongeveer $5$ %.

Ook dit kan met de standaardnormale tabel: $2*text(P)(z lt text(-)2) ~~ 2*0,228 ~~ 0,456$ . En dat is ook ongeveer $5$ %.

Schat het percentage van deze mannen dat een bloeddruk heeft van meer dan $150$ mm Hg.

$text(P)(B gt 150) = 1 - text(P)(z lt (150-128,5)/(12,5)) = 1 - text(P)(z lt 1,72) ~~ 0,0427$ , dus ongeveer $4,3$ %.

Op grond van deze steekproef van $1000$ mannen wil je de gemiddelde bloeddruk van alle Nederlandse mannen voorspellen.

Geef het bijbehorende $95$ %-betrouwbaarheidsinterval in één decimaal nauwkeurig.

Bij je voorspelling hoort $mu ~~ bar(B) = 128,5$ en $sigma ~~ s_B = 12,5$ .

Het $95$ %-betrouwbaarheidsinterval is $128,5 - 1,96*(12,5)/(sqrt(1000)) lt mu lt 128,5 + 1,96*(12,5)/(sqrt(1000))$ , dus $127,7 lt mu lt 129,3$ .

In een fabriek verpakt een machine in kleine zakjes poedermelk voor in de koffie. Elk van die zakjes hoort $3$ gram melkpoeder te bevatten. De fabrikant heeft zijn machine zo afgesteld dat het vulgewicht van deze zakjes normaal is verdeeld met een gemiddelde van $3,1$ gram en een standaardafwijking van $0,06$ gram.

Hoeveel procent van de zakjes melkpoeder die deze machine produceert, is te licht?

$text(P)(V lt 3) = text(P)(z lt (3-3,1)/(0,06)) ~~ text(P)(z lt text(-)1,67) ~~ 0,0475$ , dus $~~ 4,8$ %.

De fabrikant voldoet hiermee niet aan bepaalde richtlijnen. Die schrijven voor dat niet meer dan $1$ % van de zakjes poedermelk minder dan $3$ gram mag bevatten.

De fabrikant besluit om iets meer melkpoeder in de zakjes te doen. Op welk gemiddelde vulgewicht moet hij de machine instellen om aan de richtlijn van de EU te voldoen? Ga ervan uit dat de standaardafwijking van de verdeling van de vulgewichten hetzelfde blijft.

$P(V lt 3) = 0,01$ geeft $text(P)(z lt (3-mu)/(0,06)) = 0,01$ .

Met de $z$ -tabel: $(3-mu)/(0,06) ~~ text(-)2,33$ .

Dus $μ ≈ 3,14$ gram.

Je koopt een doosje met daarin twintig zakjes van het melkpoeder dat nog het oorspronkelijke gemiddelde van $3,1$ gram heeft.

Hoeveel gram melkpoeder verwacht je gemiddeld per zakje in het doosje met twintig zakjes? En welke standaardafwijking hoort daarbij?

Je verwacht gemiddeld $3,1$ gram met een standaardafwijking van $(0,06) / (sqrt(20)) ~~ 0,013$ gram.

Bij een steekproef van een flinke populatie is van $100$ pasgeboren baby's is de lengte (in cm) gemeten. De gemiddelde lengte in de steekproef is $bar(L) = 52,2$ cm en voor de standaardafwijking van de lengte geldt $s_L = 2,38$ .

Bereken het $95$ % betrouwbaarheidsinterval van de gemiddelde lengte van de populatie.

$95$ %-betrouwbaarheidsinterval loopt van $52,2- 1,96*(2,38)/(sqrt(100))$ tot $52,2 +1,96*(2,38)/(sqrt(100))$ .
Dus van $51,7$ tot $52,7$ cm.

Onder de metingen zit een meetfout. Een van de baby's is geen $43$ maar $49$ cm. Dit heeft gevolgen voor het gemiddelde en voor $s$ . Nu is $s_L = 1,84$ . Bereken het $95$ % betrouwbaarheidsinterval opnieuw.

Gemiddelde: alle lengtes bij elkaar is $52,2*100+6=5226$ cm.
Het nieuwe gemiddelde is dus $5226/100= 52,26$ cm.

$sigma = 1,84/sqrt(100) ~~ 0,184$

$95$ % betrouwbaarheidsinterval tussen $52,26-1,96*0,184$ en $52,26 +1,96*0,184$ , dus tussen $51,9$ en $52,6$ cm.

Leg uit waarom een meetfout in een kleine steekproef grotere gevolgen heeft voor het betrouwbaarheidsinterval dan een meetfout in een grote steekproef.

Het betrouwbaarheidsinterval verandert als het gemiddelde en/of de standaardafwijking veranderen. Bij een meetfout in een kleine steekproef, veranderen ze meer dan bij een meetfout in een grote steekproef.

Een opdrachtgever eist van een fabrikant dat het gemiddelde gewicht werkzame stof in een partij van $2000$ flessen met reinigingsmiddel $12$ gram is.

De fabrikant test dit door middel van een steekproef. Hij vindt een betrouwbaarheidsinterval met een breedte van $2$ gram voldoende precies bij een betrouwbaarheid van $95$ %.

De fabrikant weet dat de standaardafwijking van het gewicht van de werkzame stof bij zijn productieproces $4$ gram is.

De fabrikant wil weten hoe groot de steekproefomvang moet zijn om aan deze eisen te kunnen voldoen.

Bereken de minimaal benodigde steekproefomvang.

De breedte van het betrouwbaarheidsinterval moet $2$ zijn.

Dus het betrouwbaarheidsinterval is het gemiddelde $+- 1$ .

Dus $1,96*4/(sqrt(n))=1$ .

Dus $n~~62$ .

Je ziet hier een controlekaart van een fabrikant van chips.
Van alle chips mag volgens een Europese referentierichtlijn de hoeveelheid acrylamide niet hoger zijn dan $750$ µg/kg. Deze chipsfabrikant probeert zich aan die richtlijn te houden en meet elk half uur de hoeveelheid acrylamide in een steekproef uit zijn productie.

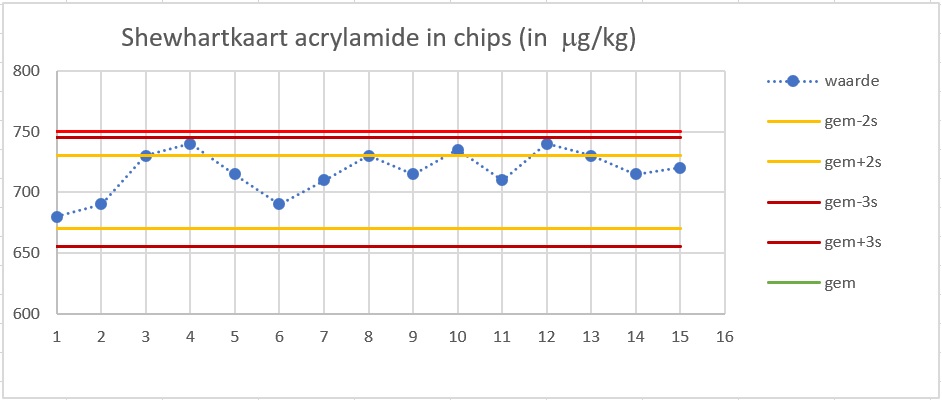
Hoeveel acrylamide bevatten zijn chips gemiddeld volgens de fabrikant?

$700$ µg/kg.

Met welke standaarddeviatie rekent de fabrikant?

$mu + 2sigma = 730$ en $mu=700$ geeft $sigma=15$ µg/kg.

Waar vind je in de figuur de Europese richtlijn terug?

Die wordt weergegeven door de rode horizontale lijn op $750$ µg/kg.

Hoe vaak wordt de bovenste waarschuwingslijn overschreden?

Echt overschreden wordt die lijn drie keer. En nog eens drie keer wordt hj bereikt.

Is er volgens deze Shewhartkaart reden om het productieproces bij te stellen? Licht je antwoord toe.

Als je de Westgardregels hanteert is alleen het aantal keren dat de hoeveelheid acrylamide achter elkaar boven $mu + 1sigma = 715$ µg/kg uitkomt zorgwekkend.