werken met de f-toets om precisie van metingen te vergelijken.
werken met de normale verdeling en Student´s t-verdeling;
de begrippen hypothese toetsen, nulhypothese, alternatieve hypothese, kritieke gebied, onterecht de nulhypothese verwerpen;
het begrip significantieniveau en de procedure bij hypothese toetsen;
linkszijdige, rechtszijdige, tweezijdige toetsen uitvoeren.
In een laboratorium wordt de pH-waarde (zuurgraad) van vloeistof in een tank gemeten. Twee laboranten doen metingen. Je ziet hier de resultaten.

De gemiddelden van deze metingen verschillen niet veel.
Maar de standaarddeviaties lopen wel wat uiteen, je vindt:
Laborant A: en .
Laborant B: en .
Toetsen van het gemiddelde, of betrouwbaarheidsintervallen voor de schatting van het populatiegemiddelde opstellen kun je met de -verdeling doen. Je zegt dan iets over de juistheid van je metingen.
Maar om vast te stellen of laborant B significant minder precies is dan laborant A gebruik je een verdeling die is bedacht door de Britse statisticus Ronald Fisher (1890 - 1962) en daarom de -verdeling heet. Daarbij gaat het om relatieve percentages die horen bij de grootheid:
waarin en de standaardafwijkingen zijn van twee metingen van dezelfde grootheid. Daarbij is altijd .
Je kunt er de -toets voor standaardafwijkingen mee uitvoeren.
Daarbij is:
: (beide standaardafwijkingen verschillen niet);
: (beide standaardafwijkingen verschillen) of : .
Hierbij bestaat een -tabel waarin je de grenswaarde van kunt opzoeken bij een gegeven betrouwbaarheid en de steekproefgroottes van de metingen A en B. Bij A hoort een vrijheidsgraad bij steekproefgrootte . Bij B hoort een vrijheidsgraad bij steekproefgrootte . In de gegeven tabel is de betrouwbaarheid %.
Bekijk de metingen van beide laboranten in de Uitleg.
Je gaat nu een -toets uitvoeren.
Leg uit, waarom hier en bereken de -waarde.
omdat .
En verder is .
In dit geval is en .
Gebruik de -tabel met betrouwbaarheid %.
Bepaal met een dubbelzijdige -toets of de precisie van beide metingen significant van elkaar verschilt.
Lees in de tabel af .
Dit betekent dat voor een -waarde van of groter de precisie van beide metingen significant van elkaar verschilt.
Voor deze metingen heb je gevonden, dus het verschil in precisie is niet significant.
Omdat bij de gegeven metingen al meteen zichtbaar is dat is ook als alternatieve hypothese : denkbaar.
Bepaal met een enkelzijdige -toets of significant groter is dan .
Lees in de tabel af .
Dit betekent dat voor een -waarde van of groter significant groter is dan .
Voor deze metingen heb je gevonden, dus is niet significant groter dan .
In de Uitleg vind je de -verdeling.
Welke waarde heeft als beide metingen even precies zijn gedaan, dus als ?
Dan is .
Bekijk de -tabel met betrouwbaarheid %.
Welke waarde benadert als zowel als heel groot worden?
Geef hiervoor een verklaring.
Dan gaat de waarde benaderen.
Dat komt omdat je de juiste waarde van de grootheid die je aan het meten bent steeds dichter benadert naarmate je steekproef groter wordt. Beide meetsessies krijgen dus steeds kleiner standaarddeviaties die ook steeds dichter bij elkaar komen.
Als je met behulp van twee series metingen A en B een bepaalde grootheid wilt vaststellen, krijg je bij A een steekproefgrootte , een gemiddelde met standaardafwijking en bij B een steekproefgrootte , een gemiddelde met standaardafwijking .
Met een
Neem aan , dan toets je
: ;
: (dubbelzijdige toets)
of
: (enkelzijdige toets).
Daarbij gebruik je de -verdeling
omdat .
Meestal neem je een betrouwbaarheid van % en daarbij hoort deze -tabel.
Je kunt ook de juistheid van beide series metingen vergelijken. Daartoe gebruik je een -toets, zie
Het gehalte stikstof in massaprocenten in een zak kunstmest is op twee manieren gemeten. Je ziet hier de resultaten:

Bereken van beide metingen het gemiddelde en de standaardafwijking. Bepaal met behulp van een -toets of de tweede manier significant minder precies is dan de eerste manier met een betrouwbaarheid van %.
Ga na:
Manier 1: en m%.
Manier 2: en m%.
Dit betekent dat .
Gebruik de -tabel met betrouwbaarheid 95%.
In dit geval zijn de vrijheidsgraden en .
Een enkelzijdige toets ligt voor de hand: : tegen : .
De tabel geeft daarbij .
De tweede manier is daarom significant minder precies.
Je ziet in
Bereken zelf de gemiddelden en de standaardafwijkingen van beide series metingen.
Dit gaat het snelst met behulp van Excel.
Denk er wel om dat je de steekproefstandaarddeviaties berekent.
Voer de (enkelzijdige) toets zelf uit met een betrouwbaarheid van %.
Ga na, dat je dezelfde waarden vindt als in het voorbeeld.
Ook hier zou je kunnen zeggen dat er tweezijdig getoetst moet worden. Het gaat immers alleen om het vergelijken van de precisie van twee meetseries, je hoeft niet van te voren al te weten dat de tweede serie minder precies is.
Laat zien, dat dit hier niet tot een andere conclusie zou hebben geleid.
De tabel geeft daarbij en nog steeds is de -waarde van de twee meetsessies groter.
Het gehalte stikstof in massaprocenten in een zak kunstmest is op twee manieren gemeten. Telkens wordt een monster eerst op de éne manier en dan op de andere manier gemeten. Je ziet hier de resultaten:

Bereken van beide metingen het gemiddelde en de standaardafwijking. Bepaal met behulp van een -toets of de tweede manier significant minder precies is dan de eerste manier met een betrouwbaarheid van %.
Bepaal met behulp van een -toets of de juistheid van beide metingen met dezelfde betrouwbaarheid significant verschilt.
Ga na:
Manier 1: en m%.
Manier 2: en m%.
Eerst toets je de precisie: .
De enkelzijdige -tabel geeft (denk om de juiste vrijheidsgraden): .
De tweede manier is daarom weer significant minder precies.
Nu toets je de juistheid.
Je kijkt daarvoor naar de serie verschillen van elk paar metingen . Zijn beide series metingen even juist, dan is . Zijn ze niet even juist dan is . Je toetst dus:
: tegen :
in een steekproef van met standaardafwijking .
De significantie is .
Voer deze dubbelzijdige toets zelf uit en trek de juiste conclusie.
Je ziet in
Waarom heb je nu twee even grote series metingen?
Om de juistheid te kunnen vaststellen moet je naar de verschillen van telkens twee metingen kijken. Dan moet je wel steeds zo'n verschil kunnen vaststellen. Daarom wordt elk monster eerst op de éne manier en dan op de andere manier gemeten.
Voer zelf de -toets uit met een betrouwbaarheid van %.
Ga na dat je hetzelfde krijgt als in het voorbeeld.
Voer zelf de -toets uit met een betrouwbaarheid van %.
Je toetst:
: tegen :
en .
Verder is , dus je gebruikt de Student-t-tabel met en een betrouwbaarheid van %.
, zodat .
Het kritieke gebied is dus .
Nu is en dit ligt niet in het kritieke gebied.
De conclusie is dat beide meetseries even juist zijn met een betrouwbaarheid van %.
| | lab.A | lab.B |
| aantal | ||
Twee laboranten hebben de nitraatconcentratie in mg/L van het grondwater op een bepaald perceel gemeten. Hier zie je de resultaten.
Kun je op grond van dit resultaat met een betrouwbaarheid van % beweren dat laborant B minder precies is geweest? Gebruik een -toets.
Je toetst : tegen : .
Dit betekent dat .
Gebruik de -tabel met betrouwbaarheid %.
In dit geval zijn de vrijheidsgraden en .
De tabel geeft daarbij .
De tweede manier is daarom niet significant minder precies.
De pH (zuurgraad) van zwemwater wordt regelmatig gemeten.
In een zwembad is de spreiding binnen de gevonden pH-waarden nogal groot en men besluit een nieuwe manier van meten te gaan hanteren. Hier zie je het verschil tussen de oude meetwaarden en de nieuwe op twee opeenvolgende dagen.

Bereken van beide series metingen het gemiddelde en de standaardafwijking.
Lijkt de nieuwe meetmethode precieser te zijn?
Je vindt:
oude methode: en .
nieuwe methode: en .
De nieuwe meetmethode lijkt inderdaad precieser.
Kun je met een betrouwbaarheid van % vaststellen dat de nieuwe meetmethode precieser is?
Je toetst : tegen : .
Dit betekent dat .
Gebruik de -tabel met betrouwbaarheid %.
In dit geval zijn de vrijheidsgraden en .
De tabel geeft daarbij .
De nieuwe meetmethode is daarom significant minder precies.
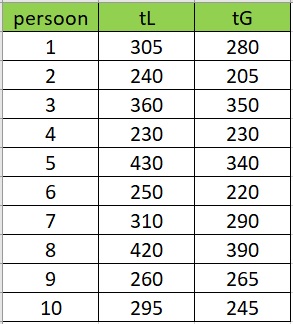
Van een tiental personen worden reactietijden gemeten.
Het is de bedoeling om de reactietijd op een geluidssignaal te vergelijken met de reactietijd op een lichtsignaal. Beide reactietijden zijn in milliseconden.
Bereken gemiddelde en standaardafwijking van beide reactietijden.
Je vindt:
oude methode: en .
nieuwe methode: en .
Kun je met een betrouwbaarheid van % vaststellen dat de reactietijden op geluid dichter bij elkaar liggen dan de reactietijden op licht? Gebruik een -toets.
Je toetst : tegen : .
Dit betekent dat .
Gebruik de -tabel met betrouwbaarheid %.
In dit geval zijn de vrijheidsgraden en .
De tabel geeft daarbij .
De reactietijden op geluid liggen dus niet significant dichter bij elkaar.
Kun je met een betrouwbaarheid van % vaststellen dat de reactietijden op geluid kleiner zijn dan de reactietijden op licht? Gebruik een -toets.
Je kijkt daarvoor naar de serie verschillen van elk paar metingen . Zijn beide series metingen even juist, dan is . Zijn de reactietijden op geluid kleiner dan is . Je toetst dus:
: tegen :
in een steekproef van met standaardafwijking (volgens Excel).
De (enkelzijdige) betrouwbaarheid is %.
, zodat .
Het kritieke gebied is dus .
Nu is (volgens Excel), en dus zijn de reactietijden op geluid gemiddeld kleiner dan die op licht.
In een medisch laboratorium worden voortdurend cholesterolgehaltes in bloedmonsters bepaald. De gebruikte apperatuur wordt elk uur gecontroleerd met
behulp van een ijkmonster. Hiervan is bekend dat het gemiddelde mg per mL zou moeten zijn met standaardafwijking mg/dL.
De controlemetingen aan het ijkmonster leveren op: , , , , , , , .
Waarom kun je in deze situatie een -toets toepassen om na te gaan of de controlemetingen even precies zijn als de standaardmetingen?
Je kunt een -toets toepassen omdat beide standaardafwijkingen bekend zijn en ook de vrijheidsgraad van de standaardmetingen bekend is, namelijk .
Is er met een betrouwbaarheid van % reden om aan te nemen dat de meetapperatuur niet nauwkeurig meer werkt?
Voor de controlemetingen geldt: en .
Je toetst : tegen : .
Dit betekent dat .
Gebruik de -tabel met betrouwbaarheid %.
In dit geval zijn de vrijheidsgraden en .
De tabel geeft daarbij .
De controlemetingen zijn inderdaad precieser dan de standaardmetingen, maar het scheelt niet veel.
In een melkfabriek worden flessen machinaal gevuld. De gedoseerde hoeveelheid per fles is normaal verdeeld. De acht flessen die de laatste uren zijn gemeten gaven een gemiddelde van g met een standaardafwijking van g. Een kwaliteitsinspecteur neemt een steekproef van flessen en vindt voor het gemiddelde g met een standaardafwijking van g.
Is er reden om aan te nemen dat deze inspecteur niet precies genoeg heeft gewerkt?
Gebruik een betrouwbaarheid van %.
De metingen van de inspecteur zijn inderdaad minder nauwkeurig dan de standaardmetingen, want .
Je toetst : tegen : .
Dit betekent dat .
Gebruik de -tabel met betrouwbaarheid %.
In dit geval zijn de vrijheidsgraden en .
De tabel geeft daarbij .
De metingen van de inspecteur zijn inderdaad minder nauwkeurig dan de standaardmetingen.
Messing is een legering van koper en zink, met soms (om bepaalde eigenschappen te bereiken) toevoegingen. In een metaalfabriek wordt messing geproduceerd met een kopergehalte dat % zou moeten bedragen.
Het kopergehalte van de geproduceerde hoeveelheid messing wordt bepaald door hetzelfde monster op twee manieren te meten.

Bepaal met % betrouwbaarheid of beide metingen even precies zijn.
Met % betrouwbaarheid zijn beide metingen even precies.
Met Excel:
oude methode: en .
nieuwe methode: en .
Dus .
Tweezijdige -toets met % betrouwbaarheid en vrijheidsgraden beide geeft .
Met % betrouwbaarheid zijn beide metingen even precies.
Bepaal met % betrouwbaarheid of beide metingen even juist zijn.
Met % betrouwbaarheid zijn beide metingen even juist.
Je kijkt naar de variabele en je toetst
: tegen :
in een steekproef van met standaardafwijking (volgens Excel).
De (dubbelzijdige) betrouwbaarheid is %.
, zodat .
Het kritieke gebied is dus .
Nu is (volgens Excel), en dus zijn beide metingen van het kopergehalte even juist.