In dit onderwerp is het trekken van conclusies uit metingen in steekproeven aan bod gekomen. Bij het doen van een uitspraak over één statistische variabele gaat het bij de juistheid om een $z$ -toets of een $t$ -toets en bij de spreiding om een $f$ -toets. Bij twee statistische variabelen gaat het om het vinden van een lineair verband tussen beide en het vaststellen van de sterkte van de samenhang.

Je hebt nu alle theorie van Conclusie trekken doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan... Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je ermee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

hypothese toetsen, enkelzijdig of dubbelzijdig significantieniveaukritieke gebiednulhypothese en alternatieve hypothesenormale toets van het gemiddelde, $z$ -toets

Student's $t$ -verdelingvrijheidsgraad $t$ -toets van het gemiddelde

Fisher's $f$ -verdeling $f$ -toets van de spreiding

spreidingsdiagram, puntenwolkcorrelatiecoëfficiënt regressielijn

het gemiddelde van een normaal verdeelde populatie toetsen met een bepaalde betrouwbaarheid als de populatiestandaarddeviatie bekend is met behulp van een steekproef;

het gemiddelde van een normaal verdeelde populatie toetsen met een bepaalde betrouwbaarheid als de populatiestandaarddeviatie niet bekend is met behulp van een kleine steekproef;

de standaarddeviaties van twee steekproeven uit een normaal verdeeld populatie met een bepaalde betrouwbaarheid vergelijken;

bij een spreidingsdiagram de correlatiecoëfficiënt berekenen en interpreterenbij een spreidingsdiagram een regressielijn berekenen en daarmee voorspellingen doen.

Volgens de informatie op een pakje drinkyoghurt zou dit gemiddeld $12,5$ gram suiker bevatten. Een onderzoeksbureau beweert dat er in werkelijkheid veel meer suiker in de pakjes zit.

De leverancier van de pakjes besluit een steekproef van $50$ pakjes te nemen. De pakjes uit de steekproef bevatten gemiddeld $16,4$ gram suiker.

Neem aan dat de hoeveelheid per pakje normaal verdeeld is met een standaardafwijking van $3,1$ gram.

Onderzoek of dit resultaat voldoende aanleiding is om de informatie die op de pakjes staat te verwerpen. Neem een significantieniveau van $1$ %.

Toevalsvariabele $S$ is de hoeveelheid suiker in een pakje drinkyoghurt.

Hypothesetoets:

$text(H)_0$ : $mu_S = 12,5$

$text(H)_1$ : $mu_S > 12,5$

Omdat de populatiestandaarddeviatie is gegeven wordt dit een $z$ -toets.

$text(P)(bar D > 16,4) = 1 - text(P)(z lt (16,4-12,5)/((3,1)/(sqrt(5)))) ~~ 0,0000$ ofwel vrijwel $0$ .

Dit is inderdaad aanleiding om $text(H)_0$ en dus ook de informatie op de pakjes te verwerpen.

$11,9$	$11,1$	$11,4$	$12,6$
$11,6$	$11,4$	$11,7$	$11,8$
$11,8$	$11,8$	$12,4$	$12,5$
$11,7$	$12,3$	$11,3$	$12,2$
$11,9$	$12,6$	$11,7$	$11,8$

Op het etiket van een pot jam staat dat het percentage rietsuiker $12,4$ % is. Om dit te controleren wordt het percentage rietsuiker van $20$ willekeurige potten jam bepaald en in een tabel gezet.

Je mag aannemen dat het percentage rietsuiker normaal verdeeld is.

Formuleer de hypothesen in deze situatie.

$text(H)_0: mu_R = 12,4$ tegen $text(H)_1: mu_R != 12,4$ .

Bereken het gemiddelde en de standaardafwijking van het percentage rietsuiker in de steekproef. Rond af op drie decimalen.

$bar(R) = 11,875$ en $s_R ~~ 0,423$ %.

Toets je hypothese met een significantieniveau $alpha = 0,10$ .

Je moet nu een tweezijdige $t$ -toets doen met $v=20-1$ en betrouwbaarheid $90$ %.

$t = (bar(R)-12,4)/((0,423)/(sqrt(20))) = +-1,73$ geeft als kritiek gebied $bar(R) lt 12,236 vv bar(R) gt 12,563$ .

De nulhypothese wordt verworpen omdat $bar(R) = 11,875$ in het kritieke gebied ligt.

Artsen schrijven aspirines voor aan hartpatiënten om te voorkomen dat bloedklonters aderen zullen verstoppen. Bij $12$ volwassen mannen is onderzocht of het gebruik van aspirines een positieve invloed heeft op klontervorming in het bloed, dat wil zeggen, dat de stollingstijd groter wordt.

De stollingstijd (in minuten) werd gemeten vóórdat de mannen aspirines innamen en drie uur na het innemen van twee aspirines, zie de tabel.

Onderzoek met behulp van een $f$ -toets of beide steekproeven even precies zijn met een betrouwbaarheid van $95$ %.

Bereken eerst de standaardafwijkingen.

stollingstijd vooraf: $s_V ~~ 0,696$ .

stollingstijd achteraf: $s_A ~~ 0,754$ .

Dubbelzijdige $f$ -tabel met $v_V=v_A=12-1=11$ en een betrouwbaarheid van $95$ % geeft $f$ tussen $3,72$ en $2,86$ .

$f = (0,754^2)/(0,696^2) ~~ 1,17$ , dus deze $f$ -waarde ligt niet in het kritieke gebied.
Beide steekproeven zijn even precies.

Onderzoek met behulp van een $t$ -toets of de stollingstijd van het bloed significant is toegenomen. Gebruik een betrouwbaarheid van $95$ %.

Het zijn gepaarde waarnemingen dus je kunt naar de verschillen $V$ tussen de stollingstijden kijken.

Het gemiddelde daarvan is $0,2$ met een standaardafwijking van $0,504$ .

Je toetst $text(H)_0$ : $bar(V) = 0$ tegen $text(H)_1$ : $bar(V) gt 0$ .

In de $t$ -tabel vind je $t=1,73$ .

$t = (bar(V)-0)/((0,504)/(sqrt(20))) = 1,73$ , dus het kritieke gebied is $bar(V) gt 0,19$ .
Omdat $bar(V) = 0,2$ zou je dus kunnen concluderen dat er inderdaad een significant verschil is.
Maar de steekproef is zo klein en het gevonden gemiddelde zit zo dicht bij de grens, dat verder onderzoek nodig is!

leeftijd	woordenschat
4	$3000$
5	$3800$
6	$4500$
7	$5200$
8	$6000$
9	$8500$
10	$11000$
11	$14000$
12	$17000$

Bekijk de tabel met de (geschatte) woordenschat die eentalige Nederlandse kinderen hebben.

Wat mag je, op basis van de gegevens uit deze tabel, concluderen omtrent het verband tussen de leeftijd en de woordenschat van een eentalig Nederlands kind? En kun je hiermee bijvoorbeeld voorspellen hoe groot de woordenschat van een volwassene is?

Er bestaat een sterke correlatie tussen leeftijd en woordenschat, zoals te zien is aan het spreidingsdiagram en de correlatiecoëfficiënt van $0,957$ .

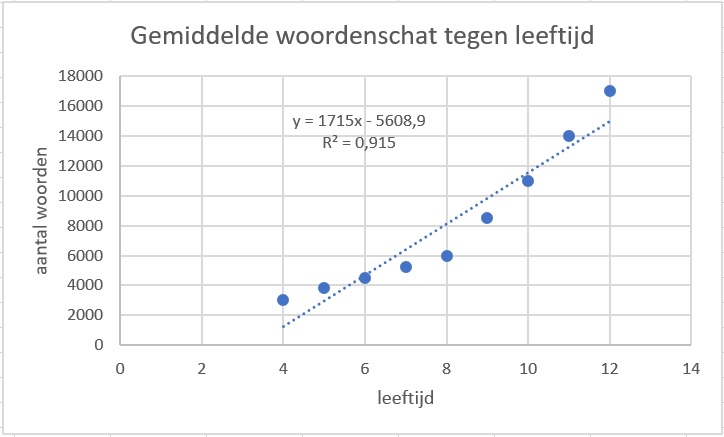
Je kunt hier echter nauwelijks voorspellingen mee doen. Veel hangt af van de verder ontwikkeling.

bron: www.cbsdeakker.nl

In 1947 hielden de wiskundigen Freudenthal en Sittig een statistisch onderzoek ten behoeve van een nieuw maatsysteem voor vrouwenkleding in opdracht van het warenhuis De Bijenkorf. Zij lieten daarbij een grote verscheidenheid aan lichaamsmaten opmeten van $5001$ vrouwen. Zij vonden onder andere een sterke correlatie tussen de taille (de omtrek van het lichaam gemeten ter hoogte van de navel) en de bovenwijdte (de omtrek van het lichaam gemeten ter hoogte van de borst). De gevonden correlatiecoëfficiënt bedroeg ongeveer $0,9058$ .
In hun rapport De juiste maat geven zij voor de bovenwijdte $b$ een gemiddelde van $97,99$ cm met een standaardafwijking van $10,12$ cm en voor de taille $t$ een gemiddelde van $80,45$ cm met een standaardafwijking van $10,80$ cm.

Welke betekenis heeft deze hoge correlatie tussen $b$ en $t$ voor een spreidingsdiagram van deze twee variabelen?

Het spreidingsdiagram bestaat uit $5001$ punten die ongeveer op een rechte lijn liggen.

Stel een vergelijking op van de regressielijn voor $b$ .

De richtingscoëfficiënt is $a=r*(s_b)/(s_t)=0,9058*(10,12)/(10,80)~~0,85$

Het begingetal is $bar(b) - a*bar(t) = 97,99-0,85*80,45~~29,61$

Regressielijn: $b = 0,85t + 29,61$

Geef een statistisch verantwoorde schatting van de bovenwijdte van een vrouw met een taille van $90$ cm.

Gebruik de formule van de regressielijn:

$b~~0,85*90+29,61 ~~ 106$ cm