datasets karakteriseren door getallen die de spreiding ervan aangeven;
spreidingsbreedte, (inter)kwartielafstand en standaardafwijking bepalen.
onderscheid maken tussen kwalitatieve en kwantitatieve statistische variabelen;
de begrippen juistheid en precisie van een steekproef;
waarnemingen weergeven in tabellen en in verschillende soorten diagrammen;
klassenindeling, klassenbreedte, absolute en relatieve frequentie.
datasets karakteriseren door getallen die het centrum ervan aangeven;
modus (modale klasse), mediaan en gemiddelde bepalen.
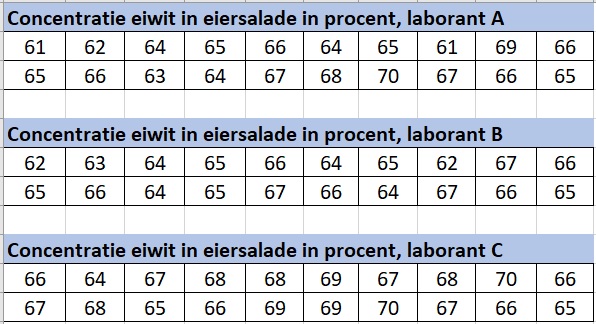
In een laboratorium wordt de hoeveelheid eiwit in eiersalade gemeten. Van een bepaalde fabrikant worden kuipjes eiersalade onderzocht. Er gaan drie laboranten mee aan het werk. Van dezelfde kuipjes meten ze onafhankelijk van elkaar het eiwitgehalte. Je ziet hiernaast de resultaten.
Je wilt deze resultaten kunnen vergelijken. Zo is dat nogal lastig, zeker als de datasets groter worden. Een manier is het gebruik van frequentietabellen en diagrammen. Maar je kunt ook werken met centrummaten en spreidingsmaten. Dan vat je de meetgegevens met twee getallen samen.
Er worden meerdere spreidingsmaten gebruikt:
de spreidingsbreedte is het verschil tussen de hoogste en de laagste waarde;
de (inter)kwartielafstand is de lengte van de box in een boxplot: ;
de gemiddelde absolute afwijking is de som van alle (positieve) afwijkingen van het gemiddelde gedeeld door het aantal waarden.
Bij laborant A is de spreidingsbreedte %, is de kwartielafstand % en is het gemiddelde absolute afwijking %.
Je noteert de gemiddelde absolute afwijking wel als
Hierin is het positieve verschil van een waarde met het gemiddelde.
In plaats van mag je natuurlijk ook een andere letter gebruiken, zoals voor eiwitgehalte.
Al deze spreidingsmaten zeggen iets over de precisie van de metingen. De relatieve spreidingsbreedte is daar (op dit moment) een goede maat voor. Je deelt dan de spreidingsbreedte door het gemiddelde van de steekproef.
Bekijk Uitleg. Je ziet meetgegevens van drie laboranten.
Reken de gemiddelde absolute afwijking van laborant A zelf na.
Je kunt dit met de hand doen door eerst het gemiddelde te berekenen, dat is .
Vervolgens bereken je bij elke meetwaarde het positieve verschil met het gemiddelde en tel je die allemaal op.
Het resultaat deel je door het aantal meetwaarden en je vindt
Als je de gegevens van laborant A in een rij (of een kolom) van Excel zet, kun je met =GEM.DEVIATIE(de gegevens) de gemiddelde absolute afwijking in één keer bepalen.
Waarom de relatieve spreidingsbreedte iets over de precisie van de metingen?
Bereken die relatieve spreidingsbreedte voor laborant A.
Dit getal vormt een maat voor hoe dicht de metingen bij elkaar liggen.
De relatieve spreidingsbreedte is %.
Dat is nogal groot!
Bereken ook van de andere twee laboranten de spreidingsbreedte, de en de
Bereken ook de precisie van die metingen.
Laborant B: spreidingsbreedte %, %,
Laborant C: spreidingsbreedte %, %,
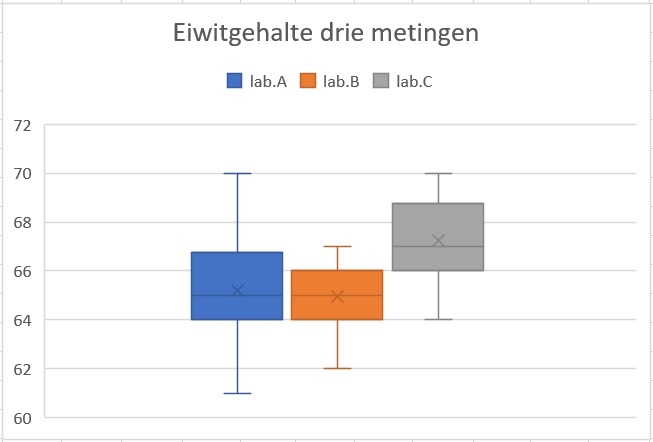
Je ziet de gegevens ook in de vorm van boxplots terug.
Laborant C ijkt zijn meetinstrument en doet de meting opnieuw. Bekijk de resultaten.

Bereken hierbij de spreidingsbreedte, de en de gemiddelde absolute afwijking.
Is het resultaat precieser of juister?
Laborant C, tweede meting: spreidingsbreedte %, %,
De relatieve spreidingsbreedte is nu %.
Het resultaat is vrijwel even precies, maar juister.
Hier zie je de de voetlengtes van mannen.
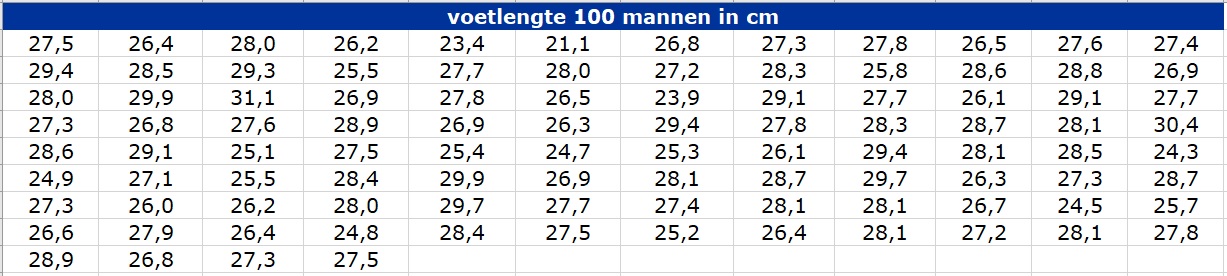
Is het gemakkelijk om uit de figuur het de drie spreidingsmaten van deze gegevens te bepalen?
Nee, je kunt beter meteen met het Excelbestand te gaan werken.
Bereken de spreidingsbreedte, de kwartielafstand en de gemiddelde absolute afwijking van de voetlengtes van deze mannen.
De spreidingsbreedte is cm, de kwartielafstand is cm en de gemiddelde absolute afwijking is cm.
In het bijgevoegde bestand vind je ook de voetlengtes van vrouwen.
Bereken de spreidingsbreedte, de kwartielafstand en de gemiddelde absolute afwijking van de voetlengtes van deze vrouwen.
De spreidingsbreedte is cm, de kwartielafstand is cm en de gemiddelde absolute afwijking is cm.
Kun je door deze spreidingsmaten bij de mannen en de vrouwen te vergelijken conclusies trekken?
De relatieve spreidingsbreedte is bij de mannen %.
De relatieve spreidingsbreedte is bij de vrouwen %.
Bij de mannen is de relatieve spreidingsbreedte veel groter, daar zijn dus echte uitschieters.
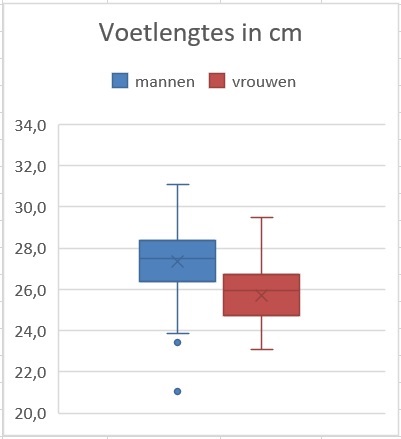
Je ziet hier twee boxplots van de gemeten voetlengtes van mannen en vrouwen. Bij de mannen zijn er twee losse datapunten te zien. Dat zijn echte uitschieters, in dit geval beide naar beneden.
In een boxplot is een uitschieter (of uitbijter) een waarde die meer dan keer de interkwartielafstand onder het eerste kwartiel of boven het derde kwartiel zit. Hier zijn het de waarden en .
Ga na dat deze waarden beide meer dan de kwartielafstand onder zitten.
In speciale gevallen bij kleine steekproeven kun je uitschieters opsporen met behulp van Dixon's Q-test. Bij meetwaarden ga je zo te werk:
Je zet eerst alle meetwaarden op volgorde van klein naar groot en bepaalt de spreidingsbreedte.
Je berekent het grootste verschil tussen twee waarden naast elkaar.
Dit getal deel je door de spreidingsbreedte en je krijgt .
Je vergelijkt met de -waarde in Dixon's tabel die je vindt bij de juiste en de gewenste betrouwbaarheid. Als dan heb je met een uitschieter te maken.
Ze kun je met een zelf gekozen (of voorgeschreven) betrouwbaarheid vaststellen of een waarde een uitschieter is.
Bekijk Uitleg.
Hier zie je de de voetlengtes van mannen.

Ga zelf na dat de waarden en uitschieters zijn bij de voetlengtes van de mannen.
De interkwartielafstand is cm.
cm ligt meer dan onder , want . Voor cm geldt hetzelfde.
In het bijgevoegde Excelbestand vind je ook de voetlengtes van vrouwen.
Ga ook na, dat er bij de voetlengtes van de vrouwen geen uitschieters zijn.
De interkwartielafstand is cm.
Naar beneden is de hoogste waarde voor een uitschieter.
Naar boven is de laagste waarde voor een uitschieter.
Er zijn bij de vrouwen geen voetlengtes die niet tussen en cm liggen.
Neem aan dat je op de gegevens in het Excelbestand ook Dixon's Q-test kunt toepassen.
Onderzoek, of de waarde cm bij de mannen ook volgens deze testmethode een uitschieter is met een betrouwbaarheid van %.
Werk met Excel, zet eerst alle gegevens van de mannen in één kolom en sorteer die kolom.
De spreidingsbreedte is .
De waarde cm ligt cm van zijn
Dus .
Kijk nu in Dixon's tabel bij en een betrouwbaarheid (CL = critical value) van %. Je vind .
Omdat heb je met een uitschieter te maken.
Je denkt dat de uitschieter bij c het gevolg kan zijn van een meetfout.
Je verwijdert hem uit de data.
Onderzoek daarna of er nog een andere uitschieter is.
De spreidingsbreedte wordt bij .
De waarde cm ligt cm van zijn
Dus .
Kijk nu in Dixon's tabel bij en een betrouwbaarheid (CL = critical value) van %. Je vind .
Omdat is er niet nog een uitschieter.
Kwantitatieve statistische gegevens (data) kun je - behalve met centrummaten - samenvatten met
de
de
de
Je noteert de gemiddelde absolute afwijking wel als
De
Bij kwalitatieve data hebben spreidingsmaten vaak geen betekenis.
Soms is er sprake van een
In een boxplot is een uitschieter een waarde die meer dan keer de interkwartielafstand onder het eerste kwartiel of boven het derde kwartiel zit.
Bij kleine steekproeven kun je (onder bepaalde omstandigheden) Dixon's Q-test toepassen.
Er kunnen meerdere uitschieters zowel naar boven als naar beneden zijn.
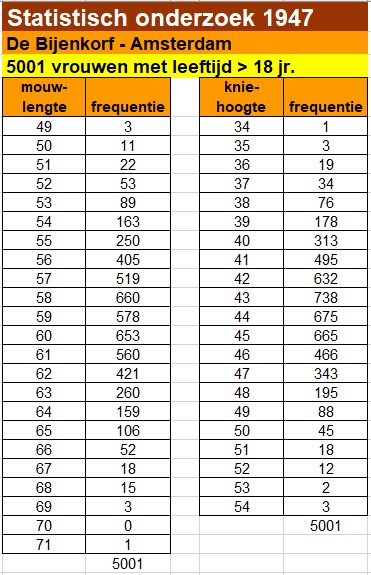
In 1947 hebben de wiskundigen Freudenthal en Sittig een grootscheeps onderzoek gehouden naar de lichaamsmaten van vrouwen in opdracht van De Bijenkorf. Daaruit wilde het bedrijf conclusies kunnen trekken betreffende de maatvoering van kleding voor hun vrouwelijke klanten.
Bepaal de spreidingsbreedte, de kwartielafstand en de gemiddelde absolute afwijking van de mouwlengtes .
Je hebt hier te maken met een frequentietabel waarbij de waarden van de statistische variabele
Omdat er vrouwen zijn opgemeten is het eerste kwartiel is het -ste getal en het derde kwartiel het -ste getal. De kwartielafstand is daarom cm.
Het berekenen van de gemiddelde absolute afwijking is nu meer werk, want je moet met de frequenties rekening houden.
Bijvoorbeeld bij een mouwlengte van cm hoort een absolute afwijking van en die komt keer voor. Je kunt dit het beste in het Excelbestand doen en Excel voor je laten rekenen.
Ga na dat
Bekijk
Ga zelf na dat de spreidingsbreedte cm, de kwartielafstand cm en de gemiddelde absolute afwijking cm is.
Werk vooral bij het berekenen van de gemiddelde absolute afwijking met Excel. Maak een extra kolom waarin een mouwlengte, het gemiddelde en de bijbehorende frequentie is. Laat Excel het rekenwerk doen.
De mouwlengte van cm lijkt een uitschieter.
Onderzoek met behulp van de kwartielafstand of dit ook zo is.
Omdat en is dit inderdaad een uitschieter.
Er zijn zo nogal wat uitschieters, naar boven en nar beneden.
Dat komt omdat de kwartielafstand erg klein is, de meetwaarden liggen in het centrum dicht bij elkaar.
Je wilt de concentratie nitraat in landbouwgrond op een bepaald stuk land vaststellen.
Je neemt monsters, waarvan je hier de resultaten ziet.
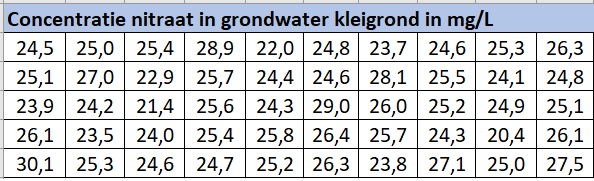
Bereken de spreidingsbreedte, de interkwartielafstand en de gemiddelde absolute afwijking.
Onderzoek ook met behulp van Dixon's Q-test of de waarde met een betrouwbaarheid van % een uitschieter is.
Je kunt dit gewoon met Excel doen: de spreidingsbreedte is , de kwartielafstand is en de gemiddelde absolute afwijking is .
Om te na te gaan of een uitschieter is, bepaal je het verschil met het getal er direct onder en dit deel je door de spreidingsbreedte: .
Je pakt nu Dixon's tabel er bij, zie het
De meetwaarde is dus geen uitschieter.
Bekijk
Bereken zelf de drie spreidingsmaten.
Werk met Excel, zie het
Voer ook zelf Dixon's Q-test uit op de meetwaarde met een betrouwbaarheid van %.
Je ziet, dat en dus is er bij deze betrouwbaarheid geen uitschieter.
Met welke betrouwbaarheid is volgens Dixon's tabel wel een uitschieter?
Met een betrouwbaarheid van (slechts) %.
Bepaal de precisie van deze metingen door de relatieve spreiding te berekenen.
De relatieve spreiding is %.
Acrylamide is een vermoedelijk kankerverwekkende stof die ontstaat in zetmeelrijke producten bij verhitting boven de °C. Voor gebakken frites is µg/kg de aanbevolen maximale hoeveelheid acrylamide. Een grote fastfoodketen laat onderzoeken of zijn frites aan dit referentieniveau voldoet. In een laboratorium worden daartoe porties frites van deze fastfoodketen onderzocht met de volgende resultaten.

Bereken de precisie van deze metingen door de relatieve spreiding te berekenen.
Het gemiddelde is µg/kg.
De spreidingsbreedte is .
De relatieve spreiding is %.
Bereken de interkwartielafstand .
µg/kg.
Is er volgens de interkwartielafstand een uitschieter bij deze metingen?
, dus is een uitschieter naar boven.
, dus er zijn geen uitschieters naar beneden.
Is er volgens Dixon's Q-test met een betrouwbaarheid van % een uitschieter bij deze metingen?
Kandidaat is de waarde . Daarvoor geldt: .
In Dixon's tabel (zie
In 1947 hebben de wiskundigen Freudenthal en Sittig een grootscheeps onderzoek gehouden naar de lichaamsmaten van vrouwen in opdracht van De Bijenkorf. Daaruit wilde het bedrijf conclusies kunnen trekken betreffende de maatvoering van kleding voor hun vrouwelijke klanten.
Bekijk de tabel van de lichaamslengte en het lichaamsgewicht van vrouwen die Freudenthal en Sittig maakten bij hun onderzoek.
Bereken de spreidingsbreedte, de kwartielafstand en de gemiddelde absolute afwijking van de lengtes.
Gebruik Excel en maak een extra kolom voor om de GAA te berekenen.
De spreidingsbreedte is cm, de kwartielafstand is cm en de GAA is cm.
Hoe groot is de relatieve spreiding van deze gegevens?
%.
Uit de wielersport komen regelmatig berichten over dopinggebruik. Wielrenners lijken
naar verboden middelen te grijpen om hun prestaties te verhogen. Een van de meest
genoemde stoffen is erytropoëtine, kortweg EPO. Dit middel bevordert de aanmaak van
rode bloedlichaampjes, waardoor de zuurstoftransportfunctie van het bloed wordt
vergroot. Je gaat hierdoor beter presteren.
De hematocrietwaarde is de
hoeveelheid rode bloedlichaampjes als percentage van de totale hoeveelheid bloed.
Die hematocrietwaarde stijgt als een wielrenner EPO gaat gebruiken.
Bij een
wielerwedstrijd in 1997 heeft men de hematocrietwaarde van een aantal wielrenners
gemeten.
De meetresultaten staan in de tabel.
Bereken de relatieve spreiding van de hematocrietwaarden van deze wielrenners.
Het gemiddelde is en de spreidingsbreedte is .
De relatieve spreiding is daarom %.
Onderzoek of een uitschieter is met behulp van Dixon's Q-test en een betrouwbaarheid van %.
.
In Dixon's tabel (zie
Je ziet hier een steelbladdiagram van een aantal snelheidsmetingen binnen de bebouwde kom van A. De maximale snelheid binnen de bebouwde kom is km/h. De politie accepteert een meetonnauwkeurigheid van km/h.
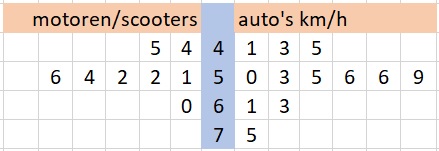
Bereken spreidingsbreedte en de kwartielafstand van de gemeten snelheden.
Spreidingsbreedte is km/h.
Kwartielafstand is km/h.
Kun je op grond van de kwartielafstand spreken van uitschieters bij deze gemeten snelheden?
en , dus er zijn geen uitschieters.
De Unox stevige erwtensoep bevat volgens het etiket % rookworst. In een laboratorium wordt dit onderzocht. Deze waarden werden in monsters aangetroffen.
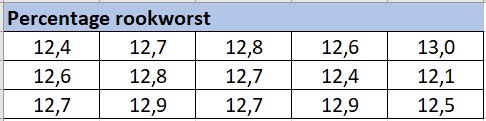
Bereken de drie spreidingsmaten.
Spreidingsbreedte , interkwartielafstand en gemiddelde absolute afwijking %.
Zeggen deze spreidingsmaten iets over de juistheid of over de precisie van de metingen?
Over de precisie.
Bereken de relatieve spreiding.
Over de precisie.
%.
Onderzoek met behulp van Dixon's Q-test of met een betrouwbaarheid van % een uitschieter is.
is een uitschieter.
en , dus ja is een uitschieter.
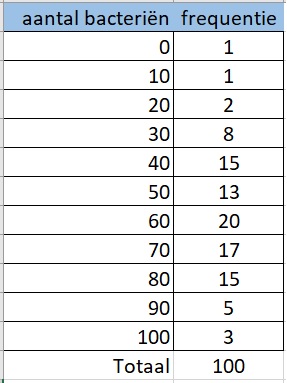
Een bedrijf haalt elke dag melk bij honderd boeren in de regio op. Voordat de melk in de transporttank gaat, wordt bij elke boer een monster van de melk genomen. In het lab wordt de melk onderzocht op het voorkomen van bacteriële vervuiling. Daartoe wordt in elk monster het aantal fecale bacteriën per centiliter geteld. De totale hoeveelheid melk die elke dag wordt opgehaald, heet een
De dienst die verantwoordelijk is voor de kwaliteitsbewaking, stelt als eis een maximum van fecale bacteriën per milliliter. In de tabel staan honderd waarden gegeven die het lab in een bepaalde dagproductie heeft gevonden.
Bereken de relatieve spreiding van het aantal bacteriën in de honderd monsters.
Zegt dit getal iets over de juistheid of over de precisie van de metingen?
Relatieve spreiding %.
Dit getal zegt iets over de precisie van de metingen, die is niet zo best.
Gemiddelde bacteriën per centiliter met spreidingsbreedte .
Dit getal zegt iets over de precisie van de metingen, die is niet zo best.
De laborante besluit de twee monsters die het laagste scoorden opnieuw te meten. Dat levert in beide gevallen een score van vijftig bacteriën op en daarmee een nieuwe dataset. Beredeneer dat in deze nieuwe set de spreidingsbreedte kleiner is dan in de oorspronkelijke dataset.
De laagste waarden worden groter.
De spreidingsbreedte is het verschil tussen de grootste en de kleinste waarde, dus als de kleinste waarde groter wordt, wordt de spreidingsbreedte kleiner.
Laat met behulp van de kwartielafstand zien, dat er in de oorspronkelijke dataset geen uitschieters voorkomen.
en .
Alle waarden blijven daar tussen.
Van gegevens die in Excel beschikbaar zijn kun je diagrammen maken en centrum- en spreidingsmaten berekenen, zie Statistiek: Data presenteren.
Voor uitschieters kun je Dixon's Q-test toepassen.