de vorm van frequentieverdelingen (ook met klassenindelingen) te typeren;
met behulp van de mediaan en het gemiddelde de scheefheid van een verdeling benoemen.
de begrippen data, populatie, steekproef, aselect en representatief, kwantitatief en kwalitatief, absolute en relatieve frequentie, discrete en continue variabele, klassenbreedte, klassenmidden en klassengrens;
werken met statistische (frequentie)tabellen en allerlei diagrammen;
centrum- en spreidingsmaten van frequentieverdelingen bepalen en die in verband brengen met de juistheid en de precisie van meetresultaten.
Bij een statistische variabele zijn veel verschillende verdelingen mogelijk.
Als je frequentieverdelingen bij datasets in beeld brengt, dus in diagrammen verwerkt, krijg je soms mooie symmetrische plaatjes, maar lang niet altijd. Sommige verdelingen zijn scheef, sommige erg grillig. Maar ook kun je met meerdere toppen te maken hebben.
Let bijvoorbeeld eens op de vorm en de verdeling van een staafdiagram. Is het diagram scheef of juist symmetrisch? Zijn er meerdere toppen of is er juist sprake van een opvallende gelijkmatigheid? Zijn er veel uitschieters?
diagram I
diagram II
diagram III
Je ziet hier diagrammen van de lengteverdeling van sporters. De lengtes zijn ingedeeld in klassen met een klassenbreedte van cm. Het meetgebied (of meetbereik) is vanaf t/m cm. Eén ervan gaat over volleyballers, één over hardlopers en één over gewichtheffers. Met behulp van de gegeven klassenmiddens kun je de mediaan en het gemiddelde van elk van deze lengteverdelingen schatten.
En aan de hand van deze centrummaten kun je goed vaststellen of een verdeling symmetrisch is of juist scheef: van een symmetrisch staafdiagram zijn gemiddelde en mediaan gelijk en zitten ze in het midden van het meetgebied, van een scheef staafdiagram zijn ze meestal verschillend en zitten ze niet in het midden van het meetbereik.
Voor lijndiagrammen en boxplots iets vergelijkbaars.
Bekijk de drie staafdiagrammen in de Uitleg.
Waarom kun je van zo'n frequentieverdeling het gemiddelde en de mediaan alleen schatten?
Door het indelen in klassen heb je de werkelijke lengtes niet meer.
Uit welke klassen bestaan deze drie lengteverdelingen?
Uit de klassen met klassenmidden , met klassenmidden , enz.
Schat met behulp van de klassenmiddens bij elk van deze drie lengteverdelingen de mediaan en het gemiddelde.
Diagram I: mediaan , gemiddelde .
Diagram II: mediaan , gemiddelde .
Diagram III: mediaan , gemiddelde .
Welke van de drie verdelingen is het meest scheef?
Licht je antwoord toe met de berekende waarden voor mediaan een gemiddelde.
Het midden van het meetbereik is .
De verdeling van diagram II is daarom het meest scheef: zowel mediaan als gemiddelde liggen daar nogal ver naast.
Welke van deze drie lengteverdelingen is meertoppig?
Waarom zal die bij de volleyballers horen?
Diagram II is tweetoppig.
Bij volleyballers heb je veel te maken met lange spelers voor het smashen/blokkeren, maar ook heeft elk team wel één of twee kleinere spelverdelers.
Je ziet hier vier zogenaamde dotplots van datasets. Elk gegeven, elk datapunt, heeft zijn eigen
Beschrijf van elke dataset de vorm van de verdeling, gebruik daarbij de mediaan en het gemiddelde.
Is er sprake van symmetrie, een gelijkmatige verdeling, meerdere toppen of uitschieters?
Dagen met hagel: meetbereik vanaf t/m , gemiddelde , mediaan , het diagram is linksscheef, rechts zitten redelijk wat uitschieters.
Gemiddelde temperatuur: meetbereik vanaf t/m , gemiddelde , mediaan , een behoorlijk symmetrische verdeling hoewel de top iets rechts van het midden van het meetbereik zit.
Dagen met strenge vorst: meetbereik vanaf t/m , gemiddelde , mediaan , erg scheve verdeling met rechts veel uitschieters.
Eruptieduur: meetbereik vanaf t/m , gemiddelde , mediaan , twee toppen, een duidelijk afwijkende verdeling.
diagram I
diagram II
diagram III
Bij de
de symmetrie
de scheefheid
het aantal toppen
de uitschieters
de gelijkmatigheid
Bij een symmetrische verdeling vallen mediaan (med) en gemiddelde (gem) vrijwel samen en zitten ze in het midden van het meetgebied (meetbereik). Dat zie je in diagram II. Soms is de verdeling scheef zoals in diagram I en soms zijn er meer toppen zoals in diagram III.
Belangrijk is wel dat je bij een frequentieverdeling met een klassenindeling de mediaan en het gemiddelde alleen nog kunt schatten met behulp van de klassenmiddens. (Tenzij je de werkelijke gegevens nog hebt!)
Voor uitschieters heb je vooralsnog een tweetal tests:
In een boxplot is een uitschieter een waarde die meer dan keer de interkwartielafstand onder het eerste kwartiel of boven het derde kwartiel zit.
Bij kleine steekproeven kun je (onder bepaalde omstandigheden) Dixon's Q-test toepassen.
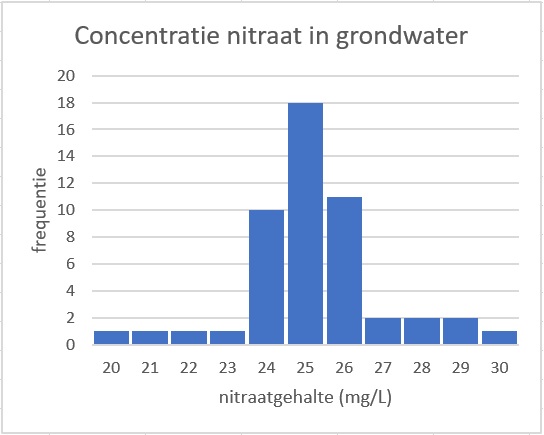
Je wilt de concentratie nitraat in landbouwgrond op een bepaald stuk land vaststellen. Je neemt monsters, waarvan je het nitraatgehalte in mg/L op één decimaal nauwkeurig vaststelt.
Om de metingen overzichtelijk weer te geven rond je ze af op gehele getallen en maak je dit staafdiagram.
Schat met behulp van dit staafdiagram de mediaan en het gemiddelde.
Is deze frequentieverdeling redelijk symmetrisch?
Er zijn metingen verricht, dus de mediaan is het gemiddelde van het ste en het ste getal. Beide getallen zijn , dus de mediaan is .
Voor het schatten van het gemiddelde maak je een frequentieverdeling.
En daarvan bereken je het gemiddelde. Ga na, dat je vind dat mg/L.
Het meetgebied loopt van tot en het midden daarvan is .
Zowel de mediaan als het gemiddelde zitten daar vlak bij.
De frequentieverdeling is eentoppig en redelijk symmetrisch.
Bekijk
Waarom kun je nu het gemiddelde en de mediaan alleen nog schatten?
Omdat je een klassenindeling hebt gemaakt door het afronden.
De klassen zijn daarom , , ..., . Je gebruikt de klassenmiddens om mediaan en gemiddelde te berekenen, maar dat zijn niet de werkelijke meetwaarden.
Bepaal zelf de mediaan en het gemiddelde.
Ga na dat de in het voorbeeld gegeven waarden kloppen.
Voer uit wat er in het
Hoeveel procent van de meetwaarden is kleiner dan (afgerond) mg/L?
Dat zijn van de meetwaarden, dus %.
Voldoet deze verzameling metingen aan de eis dat de relatieve spreiding maximaal %?
De relatieve spreiding is de spreidingsbreedte gedeeld door het gemiddelde, uitgedrukt in procenten.
Hier is de relatieve spreiding dus %.
Dus aan die eis wordt zeker niet voldaan.
Zijn er uitschieters als je werkt met de kwartielafstand?
De kwartielen zijn en .
De kwartielafstand is dus .
Uitschieters zijn waarden die meer dan keer de kwartielafstand onder of boven zitten. Dus zijn en uitschieters.
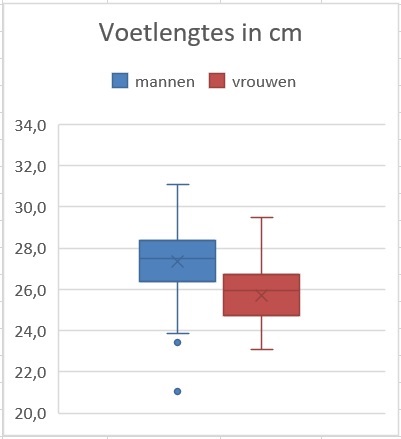
Je ziet hier twee boxplots van de gemeten voetlengtes van mannen en vrouwen. Bij de mannen zijn er twee losse datapunten te zien. Dat zijn echte uitschieters, in dit geval beide naar beneden.
De gemiddelde voetlengte van deze mannen is cm, van de vrouwen is dat cm.
Als je de uitschieters meerekent, welke van beide frequentieverdelingen is dan het meest scheef? En als je de twee uitschieters weglaat?
Uit deze figuren kun je aflezen - zelfs als je de oorspronkelijke data niet meer zou hebben - dat het meetgebied van de mannen ongeveer vanaf tot en met loopt. Bij de vrouwen is dat vanaf tot en met .
Je leest af: bij de mannen is de mediaan en bij de vrouwen cm.
Conclusie:
Bij de mannen liggen mediaan en gemiddelde ruim boven het midden van het meetgebied. Daar is van een scheve frequentieverdeling sprake.
Bij de vrouwen liggen mediaan en gemiddelde precies in het midden van het meetgebied. Daar is van een redelijk symmetrische frequentieverdeling sprake.
Laat je bij de mannen de twee uitschieters naar beneden weg, dan ziet dit er anders uit.
Ga dat zelf na.
Bekijk
Nu laat je de twee uitschieters weg.
Wat betekent dit voor de gemiddelden en de medianen?
Het gemiddelde van de mannen zal iets omhoog gaan, want er verdwijnen twee erg kleine waarden. De mediaan van de mannen zal ook iets opschuiven, maar vermoedelijk weinig veranderen. Het gemiddelde en de mediaan van de vrouwen veranderen natuurlijk niet.
Wat betekent dit voor het meetgebied van de mannen?
Dat loopt dan vanaf tot en met cm.
Welke conclusie betreffende de verdelingen trek je nu?
Het midden van het meetgebied is nu . Dus:
Bij de mannen liggen mediaan en gemiddelde nauwelijks boven het midden van het meetgebied. Daar is de verdeling redelijk symmetrisch geworden.
Bij de vrouwen liggen mediaan en gemiddelde iets onder het midden van het meetgebied. Daar is de frequentieverdeling nu enigszins scheef geworden.
Hieronder zie je een zestal frequentieverdelingen. Als er geen getal voor de frequentie is gegeven, hoort de bijbehorende waarde niet tot het meetgebied van de frequentieverdeling.

Welke van deze verdelingen zijn symmetrisch?
Symmetrisch: A, B, en C.
Welke van deze verdelingen zijn eentoppig?
Eentoppig: A, B, C, E en T.
Welke van deze verdelingen zijn links scheef?
Links scheef: E.
Bij welke van deze verdelingen is de mediaan kleiner dan het gemiddelde?
Mediaan kleiner dan gemiddelde: F.
Mediaan is , gemiddelde .
Bekijk deze boxplots. Ze stellen acht frequentieverdelingen voor waarvan het meetgebied de spreidingsbreedte is.
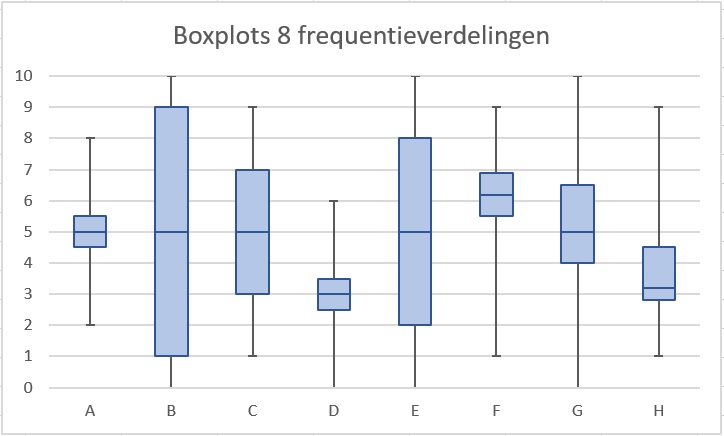
Welke van deze verdelingen zijn symmetrisch?
Symmetrisch: A, B, C, D en E.
Welke van deze verdelingen zijn links scheef?
Links scheef: H.
Welke van deze verdelingen bevatten één of meer uitschieters als je kijkt naar de interkwartielafstand?
Uitschieters: A, D, F, G en H.
Bekijk de twee staafdiagrammen.
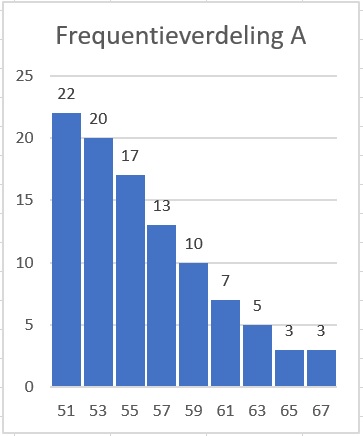
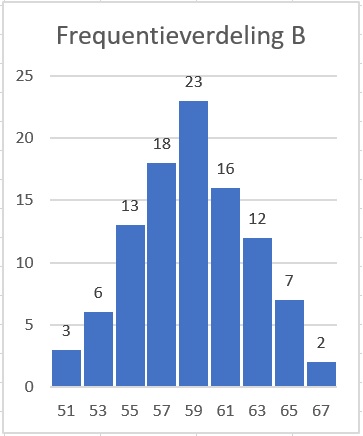
Welke klassenindeling is er gemaakt?
Welke getallen zijn de klassenmiddens?
Klassenindeling , , ..., .
Klassenmiddens: .
Maak bij elk van deze verdelingen een boxplot.
Bereken eerst de daarvoor noodzakelijke getallen.
Gebruik de klassenmiddens, behalve bij het minimum en het maximum.
Frequentieverdeling A: minimum , , mediaan , , maximum .
Frequentieverdeling B: minimum , , mediaan , , maximum .
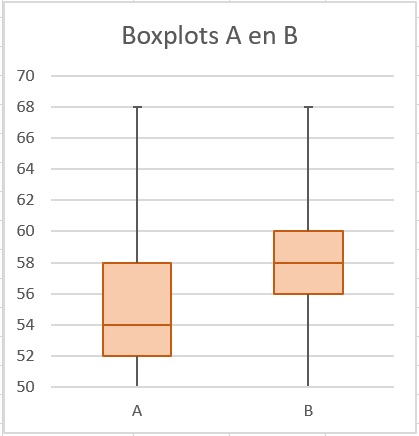
Waarom kun je bij beide verdelingen het gemiddelde alleen schatten?
Bepaal die gemiddelden en laat daarmee zien dat de verdeling B vrijwel symmetrisch is.
Je hebt de werkelijke meetgegevens niet meer, ze zijn in klassen ondergebracht.
Het gemiddelde van verdeling A is .
Het gemiddelde van verdeling B is en de mediaan is , dus die zitten vlak bij elkaar.
In ziekenhuizen worden vaak medische rapporten geschreven. Bij een onderzoek naar de inhoud van dergelijke rapporten zijn rapporten van het Elkerliek Ziekenhuis (ELK) in Deurne vergeleken met rapporten van het Academisch Ziekenhuis Maastricht (AZM). Van elk rapport is de lengte bepaald; de lengte van een rapport is het aantal woorden dat het bevat. In de figuur zijn de gegevens weergegeven in een gecombineerd staafdiagram met klassenbreedte .
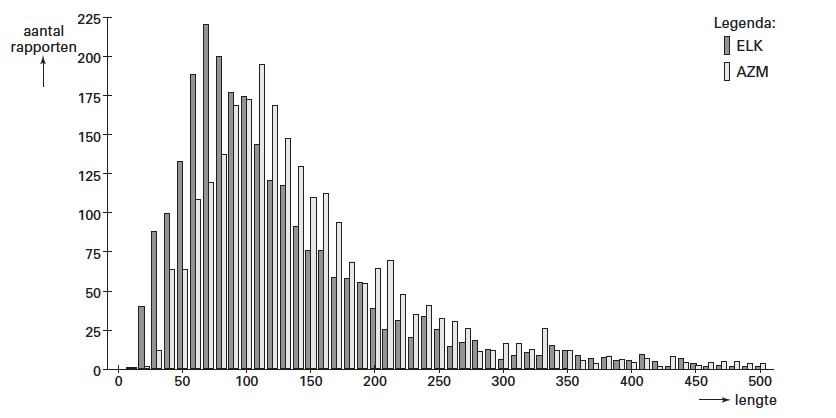
Beschrijf de overeenkomst in de vorm van de twee verdelingen.
Beide zijn scheef met één top en de uitlopers in de staart naar rechts.
Welke van deze boxplots, I of II, hoort bij de rapporten van het ELK? Licht je antwoord toe.

De verdeling van het AZM ligt ten opzichte van het ELK naar links; het 1
Kun je op grond van de twee boxplots concluderen dat er een verschil is tussen de lengtes van de rapporten in de twee ziekenhuizen? Beargumenteer je antwoord.
Kijkend naar de boxplots is er een verschil. Of het verschil typerend is voor de twee ziekenhuizen hangt af van de manier waarop de steekproef is genomen. Het aantal rapporten () is vergelijkbaar en vrij groot en hierdoor lijkt het AZM bondiger, want gemiddeld minder woorden. Pas op: het aantal woorden zegt niets over de moeilijkheidsgraad en de begrijpelijkheid van de rapporten. Het kan best zijn dat het AZM langere en moeilijkere woorden gebruikt.
Uit het onderzoek bleek dat de mediaan en het gemiddelde die horen bij de rapporten van het AZM niet even groot zijn. Geef met een redenering, dus zonder een berekening, aan of de mediaan groter of kleiner is dan het gemiddelde.
Rechts van de mediaan liggen de gegevens verder uit elkaar dan links van de mediaan. De mediaan is daarom kleiner dan het gemiddelde.
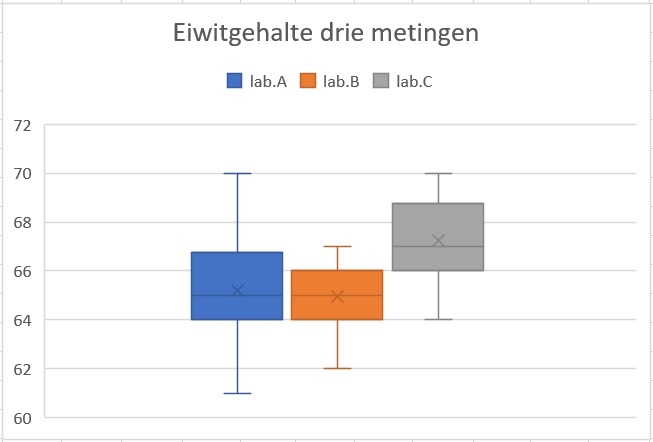
Je ziet hier boxplots van de metingen van het eiwitgehalte in eiersalade door drie verschillende laboranten. Het meetgebied is vanaf % tot en met %. De gemiddelden worden met een kruisje aangegeven.
Lees van alle drie de metingen de mediaan en het gemiddelde af.
Lab.A: mediaan %, gemiddelde %.
Lab.B: mediaan %, gemiddelde %.
Lab.C: mediaan %, gemiddelde %.
Welke verdeling is - gezien het meetgebied - het meest scheef?
De meting van laborant C.
Je ziet drie grafieken van een animatie van het CBS (Centraal Bureau voor de Statistiek). Het zijn staafdiagrammen die de verdeling van het besteedbaar inkomen in Nederland in 2007 in kaart brengen voor verschillende inkomensgroepen.
Het lichtblauwe staafdiagram gaat over het besteedbaar inkomen van alle Nederlanders.
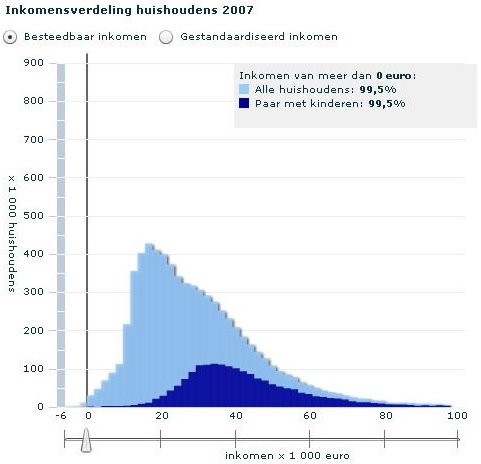
Hoe groot is het modale inkomen van de Nederlanders?
Hoeveel huishoudens betrof dat in 2007?
Dat waren ongeveer huishoudens.
Was het gemiddelde inkomen van de Nederlanders hoger of lager?
Licht je antwoord toe.
Hoger, want veel meer dan de helft van de Nederlanders verdient meer.
Beschrijf de vorm van deze lichtblauwe inkomensverdeling. Geef een verklaring.
De verdeling is linksscheef, dus met een staart naar rechts.
De inkomensverdeling is ongelijk, veel mensen verdienen een modaal inkomen of iets meer. Maar er zijn ook behoorlijk wat mensen die (heel) veel meer verdienen en dat zorgt voor een staart naar rechts.
Alle huishoudens (lichtblauw): scheef met staart rechts.
Paar met kinderen: scheef met staart rechts.
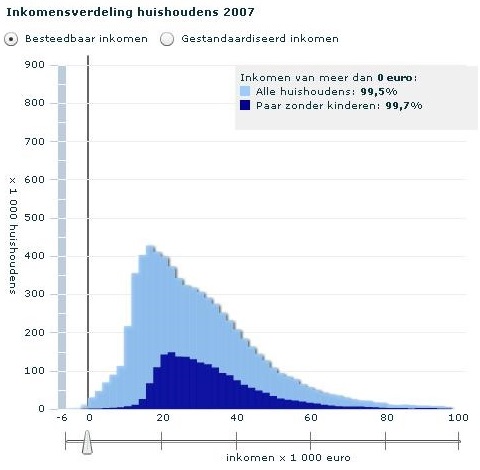
Paar zonder kinderen: nog veel schever met lange staart rechts.
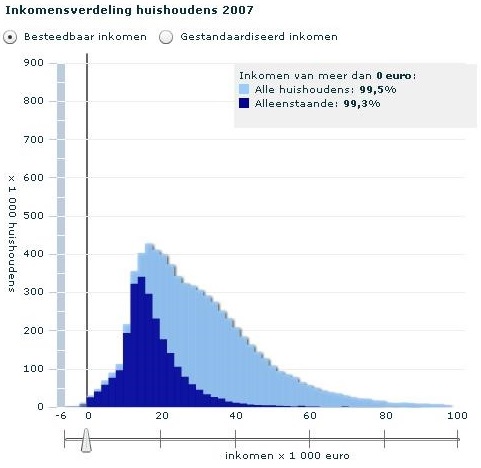
Alleenstaande: symmetrisch met één top (klokvorm).
Bekijk nu de drie donkerblauwe verdelingen.
De verdelingen van de inkomens van een paar met en een paar zonder kinderen lijken nogal op elkaar. Wat is het kenmerkende verschil en waardoor komt dat?
De besteedbare inkomens van een paar met kinderen zijn over het algemeen hoger. Dat komt waarschijnlijk doordat paren gemiddeld vaak kinderen krijgen als hun salarisniveau zo hoog is dat zie die kinderen ook kunnen onderhouden.
De inkomensverdeling van alleenstaanden is redelijk symmetrisch en zit nogal in de hoek van de lage besteedbare inkomens. Probeer dit te verklaren.
Alleenstaanden verdienen een stuk minder, wat logisch is want in een eenpersoons huishouden komt minder geld binnen, dan wanneer je met z'n tweeën werkt. Dat die verdeling redelijk symmetrisch komt omdat jongeren vaak nog alleenstaand zijn en ouderen vaak niet meer.
Beschrijf de klassenindeling die is gebruikt en geef de klassenmiddens.
Leg uit waarom je gemiddelde en mediaan van deze verdelingen alleen kunt schatten.
De klassenindeling is , , , , enz. De klassenmiddens zijn , , , , , etc.
Je kunt mediaan en gemiddelde alleen schatten omdat er van een klassenindeling sprake is.
Van gegevens die in Excel beschikbaar zijn kun je diagrammen maken en centrum- en spreidingsmaten berekenen, zie Statistiek: Data presenteren.
Voor uitschieters kun je Dixon's Q-test toepassen.