werken met regelkaarten zoals de Shewhartkaart.
de standaardafwijking van een frequentieverdeling uitrekenen en interpreteren;
een percentage onder een normale verdeling berekenen, werken met de vuistregels van een normale verdeling.
Om de kwaliteit van bepaalde processen te bewaken worden vaak controlekaarten gebruikt. Vaak worden ze Shewhartkaarten genoemd naar de Amerikaanse statisticus Walter Andrew Shewhart (1891-1967).
Je ziet hier een Shewhartkaart met de resultaten van metingen van de nitraatconcentratie in grondwater van kleigrond in een bepaald gebied in mg/L. De gemiddelde concentratie is mg/L met een standaardafwijking van .
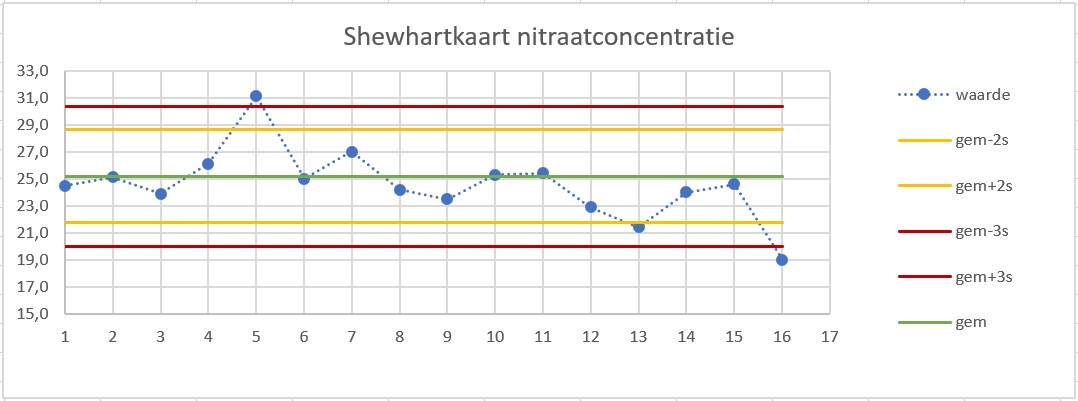
De groene lijn geeft hier het gemiddelde van de nitraatconcentratie weer. De twee oranje lijnen liggen op een afstand van en de twee donkerrode lijnen liggen op van het gemiddelde. Deze Shewhartkaart is op de vuistregels van de normale verdeling gebaseerd.
Vaak tref je op de horizontale as de tijdstippen van de metingen aan.
Omdat volgens de vuistregels van de normale verdeling slechts % van de metingen boven de bovenste oranje lijn ligt, zijn waarden die daar uitkomen bijzonder en wordt je gewaarschuwd dat er iets aan de hand kan zijn. De oranje lijnen heten daarom de waarschuwingsgrenzen van de controlekaart.
Omdat volgens de vuistregels van de normale verdeling vrijwel geen metingen boven de bovenste donkerrode lijn liggen, zijn waarden die daar uitkomen heel bijzonder en is het vrijwel zeker dat er iets aan de hand is. De donkerrode lijnen heten daarom de actiegrenzen van de controlekaart.
Bij dergelijke controlekaarten heeft James Westgard (1941-heden) regels opgesteld om aan te geven wanneer actie gewenst is. Dat zijn de Westgardregels, zie
Een Shewhartkaart kun je zelf maken, zowel met de hand als met behulp van Excel, zie het
Bekijk de controlekaart in de Uitleg.
Welke waarde voor de nitraatconcentratie hoort er bij de bovenste waarschuwingsgrens?
En bij de onderste waarschuwingsgrens?
Bij de bovenste waarschuwingsgrens hoort
mg/L.
Bij de onderste waarschuwingsgrens hoort
mg/L.
Welke waarde voor de nitraatconcentratie hoort er bij de bovenste actiegrens?
En bij de onderste actiegrens?
Bij de bovenste waarschuwingsgrens hoort
mg/L.
Bij de onderste waarschuwingsgrens hoort
mg/L.
Waarom moet je bij meting 5 in actie komen?
Deze meting ligt boven de -grens vanaf het gemiddelde.
Hij is zo uitzonderlijk dat dit waarschijnlijk geen toevallige afwijking is. Er is dus vermoedelijk iets aan de hand dat nader moet worden bekeken.
Bij welke meting wordt de -grens overschreden, maar de -grens niet?
Bij meting 13.
Het stikstofgehalte van een bepaalde kunstmest is gemiddeld m% met een standaarddeviatie van . Dit stikstofgehalte wordt regelmatig gecontroleerd. Hier zie je een tiental metingen van het stikstofgehalte in controlemonsters.

Maak hierbij zelf een Shewhartkaart.
Als het goed is krijg je deze Shewhartkaart stikstofgehalte kunstmest.
Waaraan zie je dat deze meetwaarden allemaal aan het opgegeven gemiddelde en standaarddeviatie voldoen?
Alle gegevens blijven binnen de -grenzen om het gemiddelde.
Bovendien schommelen ze netjes om het gemiddelde heen en weer, ze blijven niet allemaal boven (of allemaal onder) het gemiddelde zitten.
Bij welke meetwaarden moet je nagaan of het productieproces wel klopt?
Bij waarden boven m% of onder m%.
Om de kwaliteit van bepaalde processen te bewaken worden vaak

De horizontale lijnen hebben vaak met de vuistregels van de normale verdeling te maken:
De middelste (hier groene) lijn bepaalt het gemiddelde .
De onderste en de bovenste
Daartussen zit % van de metingen.
De onderste en de bovenste
Daartussen zitten vrijwel alle metingen.
Soms zijn er ook onderste en de bovenste
Gebeurt dit wel dan is er een onbruikbaar product ontstaan.
Bij dergelijke controlekaarten heeft James Westgard (1941-heden) regels opgesteld om aan te geven wanneer actie gewenst is. Dat zijn de Westgardregels, zie
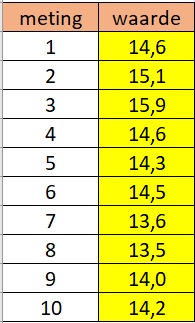
Je moet de productie van een nieuw soort kunstmest controleren op het stifstofgehalte (in m%). Omdat er geen gegevens vooraf beschikbaar zijn, doe je eerst een steekproef van monsters. Daarvan is het gemiddelde stikstofgehalte m% met een standaarddeviatie van . Deze waarden gebruik je om je controlekaart te maken.
Daarna ga je het proces bewaken, om het uur meet je het stifstofgehalte van een monster. Hiernaast zie je de eerste metingen.
Maak een bijpassende controlekaart.
Als een meting meer dan standaardafwijkingen van het gemiddelde zit spreek je van het overtreden van de -regel. Bij welke meting is dat het geval?
Als twee metingen na elkaar tussen de en standaardafwijkingen van het gemiddelde zitten spreek je van het overtreden van de -regel. Bij welke metingen is dat het geval?
Je neemt nu aan dat m% en .
Dat levert deze Shewhartkaart op:
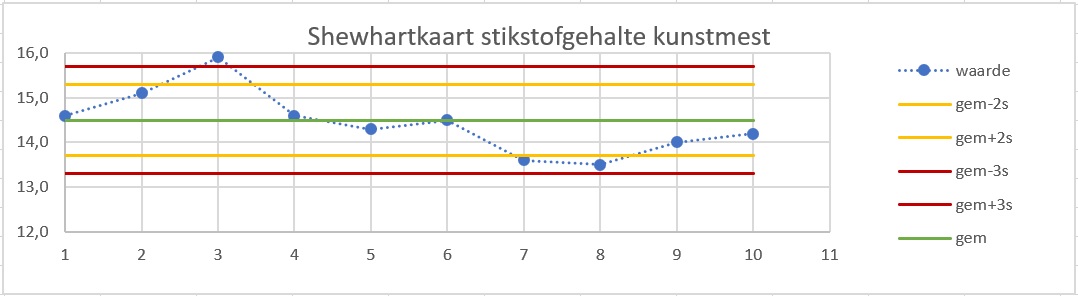
De -regel wordt overtreden bij de derde meting.
De -regel wordt overtreden bij de zevende en de achtste meting.
Bekijk
Maak zelf deze controlekaart.
Ga in het
Welke acties ga je ondernemen bij het overtreden van de - of de -regel?
Bijvoorbeeld:
de meting herhalen;
onderzoek doen naar de oorzaak;
na opheffen van de oorzaak de meting herhalen;
een nieuwe kaart starten.
Als metingen direct na elkaar allemaal meer dan onder of boven het gemiddelde liggen, spreek je van het overtreden van de -regel. Is daar sprake van?
en .
Nooit wordt bij de tien metingen de -regel overschreden.
Een buizenfabriek produceert buizen van cm met een toegestane tolerantie van mm, zowel naar boven als naar beneden. Elke dag wordt steekproefsgewijs de lengte van van die buizen nagemeten. De meetresultaten van de afgelopen week uitgedrukt in cm zijn:
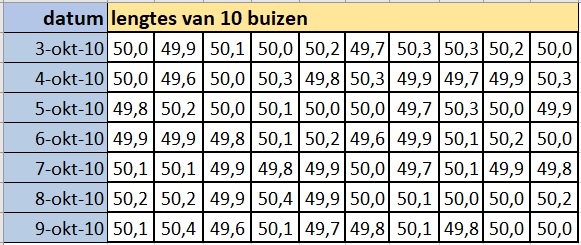
Een samenvatting van de meetresultaten zie je in deze regelkaart. De rode stippen zijn de berekende gemiddelden en de verticale lijntjes geven de minima en de maxima aan. Op de verticale as staat de buislengte. De blauwe lijnen zijn tolerantiegrenzen, de rode stippellijnen de actiegrenzen.
Met welke gemiddelde buislengte en welke standaardafwijking wordt hier gerekend?
Wat is de betekenis van de tolerantiegrenzen?
De gemiddelde buislengte wordt met de rode lijn weergegeven, dus .
De actiegrenzen liggen op een afstand van van het gemiddelde.
De bovenste actiegrens is ongeveer , dus en .
De tolerantiegrenzen zijn waarden die absoluut niet mogen worden overschreden. Bijvoorbeeld is een buis die dikker is dan cm niet bruikbaar. Hetzelfde geldt voor een buis die dunner is dan cm.
Bekijk
Een week later ziet de regelkaart er uit zoals hiernaast.
Waarom is er nu reden tot zorg, terwijl de minima en maxima toch binnen de regelgrenzen liggen? Is er nog steeds sprake van een statistisch beheerst proces?
Het gemiddelde wijkt steeds meer af van het gewenste gemiddelde en neemt steeds meer toe. Dit is geen statistisch beheerst proces, want er lijkt sprake van een systematische toename van de buisdikte.
Frederik zegt dat het proces statistisch beheerst verloopt als er maar één meting van de steekproef buiten de regelgrenzen valt. Klopt dat?
Nee, zie het antwoord bij a.
Als metingen direct na elkaar allemaal meer dan onder of boven het gemiddelde liggen, spreek je van het overtreden van de -regel. Is daar sprake van?
Ja, want het gaat in dit geval om metingen boven of onder . En de laatste metingen liggen allemaal op of zelfs daarboven.
In de praktijk worden ook regelkaarten zoals hieronder gebruikt:
met een diagram waarop alleen het gemiddelde staat;
daaronder een diagram met alleen de spreidingsbreedte .
Waarom heeft de spreidingsbreedte maar één actiegrens?
De spreidingsbreedte is groter of gelijk aan nul; een te kleine spreiding kan niet, omdat juist een zo klein mogelijke spreiding gewenst is.
Op welke hoogte ligt die actiegrens? Waarom deze hoogte? Leg uit dat die hoogte overeen komt met de actiegrenzen voor het gemiddelde.
Bij en dat is keer de standaardafwijking. De afstand in het bovenste deel van de grafiek tussen de twee stippellijntjes is even groot als de hoogte waarop de onderste stippellijn ligt.
Beredeneer dat het proces in het gedeelte van de regelkaart van dag 1 tot dag 11 statistisch beheerst is.
Tot en met dag 10 schommelt het gemiddelde mooi om het gewenste gemiddelde.
Waarom kun je zeggen dat het proces in het tweede deel van de regelkaart statistisch onbeheerst wordt?
De steekproefgemiddelden beginnen systematisch van het gemiddelde
Beschrijf een paar situaties waarin een regelkaart van deze soort aanleiding geeft om te denken dat het productieproces statistisch onbeheerst is.
Bijvoorbeeld:
Als er een waarde boven de bovenste actiegrens of onder de onderste actiegrens uitkomt.
Als de steekproefgemiddelden systematisch oplopen (of kleiner worden).
Als de spreiding boven de actiegrens komt te liggen.
...
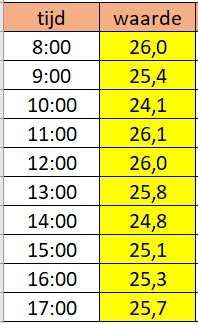
Een vulmachine vult flesjes water. Een aselecte steekproef van flesjes geeft een gemiddelde inhoud van cL. De standaardafwijking is .
Vervolgens wordt er elk uur een flesje onderzocht op de inhoud. Hier zie je de metingen van één dag.
Maak een Shewhartkaart voor het vulproces van deze machine, gebaseerd op deze gegevens en de verrichte metingen.
Zie figuur.
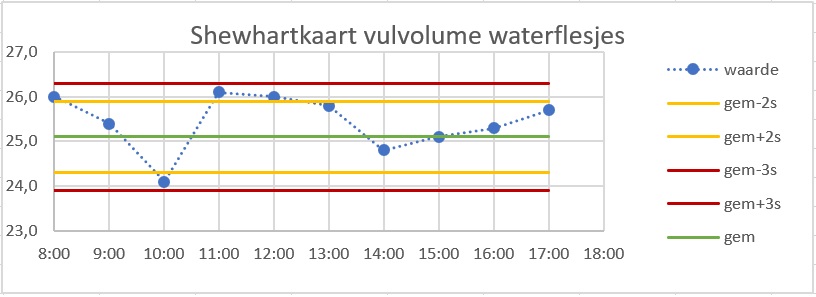
Op welke hoogte liggen beide waarschuwingsgrenzen?
Bij de bovenste waarschuwingsgrens hoort de waarde .
Bij de onderste waarschuwingsgrens hoort de waarde .
Op welke hoogte liggen beide actiegrenzen?
Bij de bovenste actiegrens hoort de waarde .
Bij de onderste actiegrens hoort de waarde .
Als twee opeenvolgende metingen meer dan van het gemiddelde afwijken dan wordt er normaal gesproken actie ondernomen. Op welk moment is dat hier het geval?
Om 12:00 uur.
Je ziet hier een controlekaart voor de productie van eiersalade. Het eiwitgehalte wordt elk half uur gecontroleerd, deze metingen zijn van één dag.
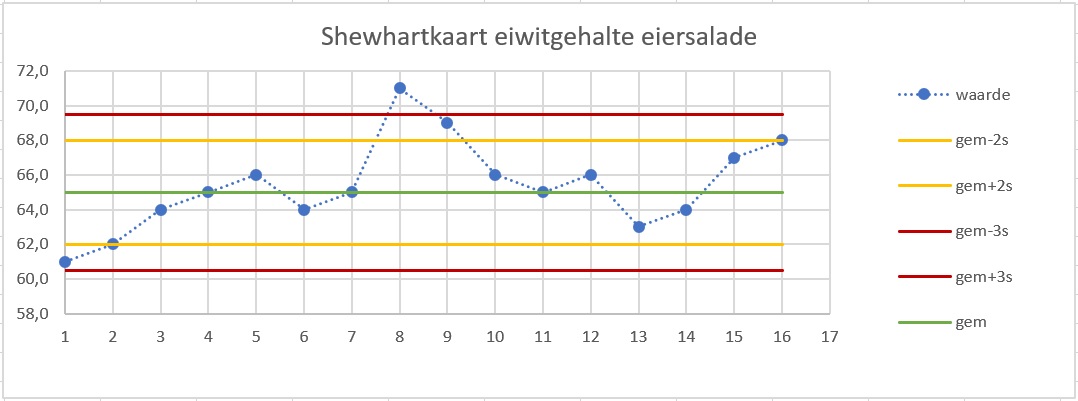
Met welk gemiddelde en welke standaardafwijking wordt er gerekend?
% en , dus .
Welke meting is onacceptabel en vereist onmiddellijke actie?
Meting 8, daarbij wordt zelfs de actiegrens behoorlijk overschreden. Voor de consument misschien prima, voor de fabrikant waarschijnlijk niet.
Bij de productie van literpakken melk is een vulmachine zo ingesteld dat de inhoud van elk pak liter is met een standaardafwijking van liter.
Om zijn productieproces te bewaken wordt er een regelkaart ontworpen. De actiegrenzen worden zo gekozen dat vrijwel alle vulvolumes daar binnen vallen. Door de wetgever is echter vastgesteld dat het vulvolume van een pak niet meer dan % onder de gewenste liter mag zitten.
Waarom is er nu maar één tolerantiegrens?
Wettelijk is er geen maximum, dus er mag best teveel melk in een pak zitten.
Maak een regelkaart voor deze fabrikant. Neem als tolerantiegrens van het gemiddelde het door de wetgever vastgestelde minimale vulvolume.
Zie figuur bij c. De onderste tolerantiegrens zit bij % van liter en dat is liter. Vuistregels normale verdeling: tussen en zit vrijwel alles, dus:
de bovenste actiegrens zit bij liter;
de onderste actiegrens zit bij liter.
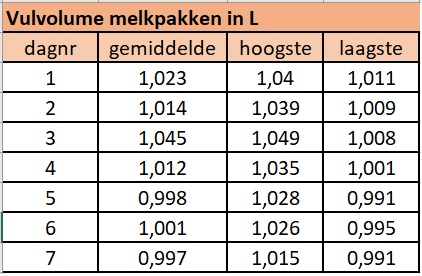
Dagelijks laat de fabrikant een steekproef trekken uit zijn pakken melk: hij laat dan van pakken melk het vulvolume bepalen. Deze tabel geeft de gemiddelden en de hoogste en laagste gemeten waarden per dag. In de controlekaart geef je met verticale lijnstukken de spreidingsbreedte van de metingen weer. Daarop zet je ook het gemiddelde.
Maak het complete diagram.
Zie figuur.
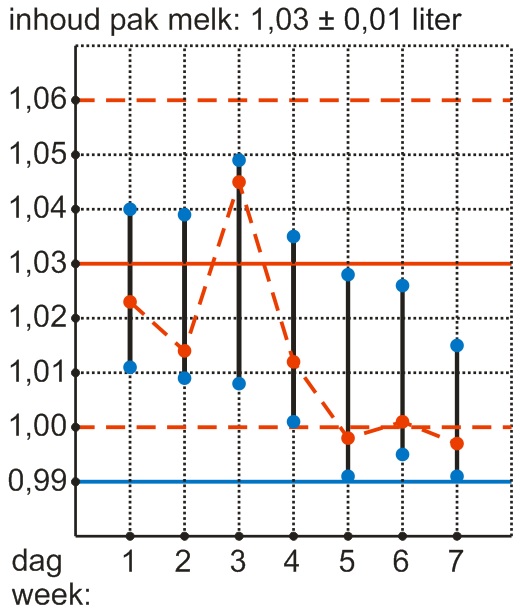
Welke conclusie zal de fabrikant trekken? Motiveer je antwoord.
Het proces zal bijgesteld moeten worden. De laatste drie metingen zitten onder de actiegrens (hoewel ze nog wel net aan het wettelijk minimum voldoen).
Hier zie je een Engelstalige controlekaart, een -regelkaart.
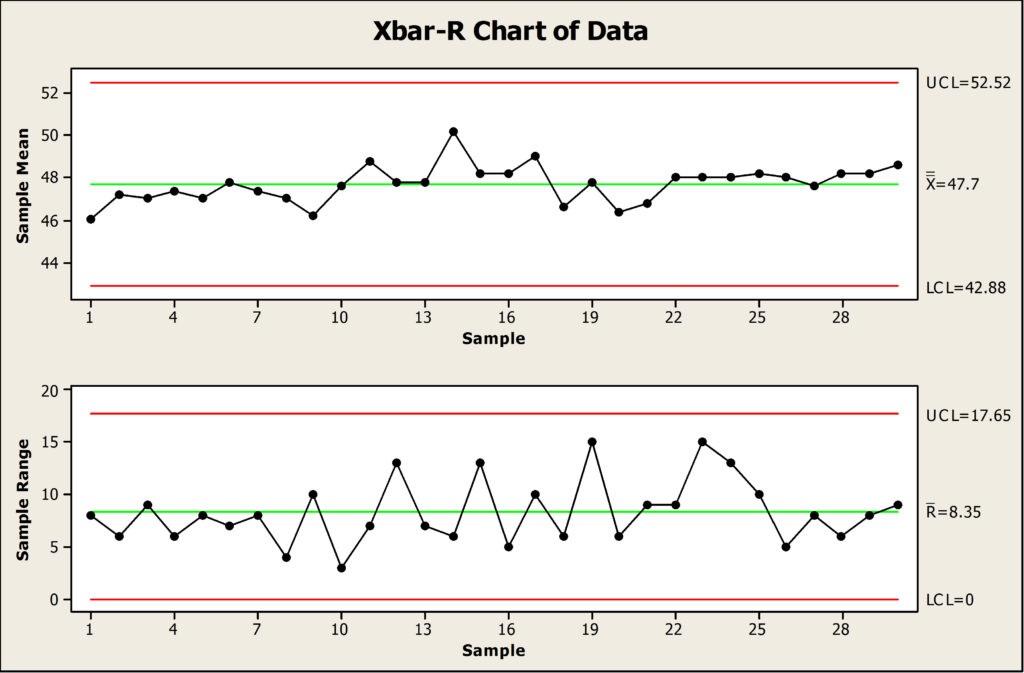
Hoe groot zijn het gemiddelde en de bijbehorende standaardafwijking die op deze regelkaart worden gebruikt?
en , dus .
Hoe groot zijn gemiddelde en standaardafwijking van de spreidingsbreedtes ?
en , dus .
Hier komt de standaardafwijking bij de spreidingsbreedtes niet overeen met de standaardafwijking van de gemiddelden. Hoe kan dat?
Kennelijk liggen de meetwaarden zelf meer verspreid dan hun gemiddelden.
Je ziet hier een statistische controlekaart over het vulgewicht (in kg) van pakken suiker.
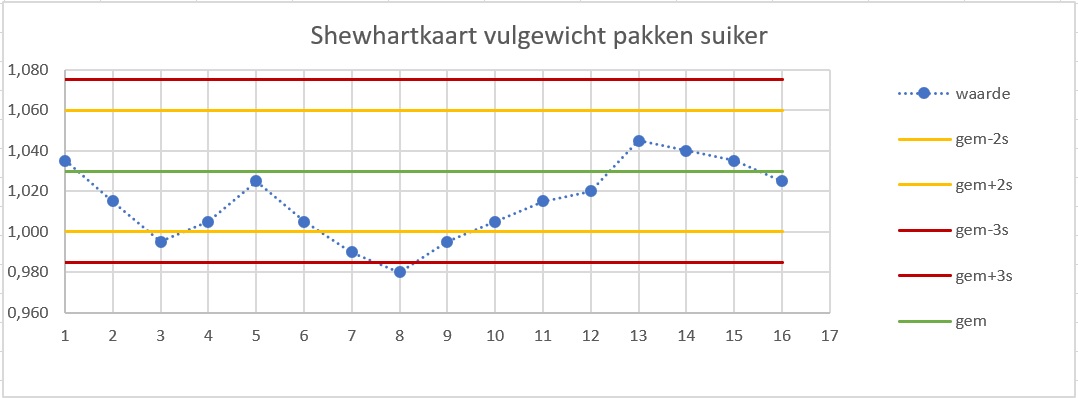
Met welk gemiddelde en welke standaardafwijking wordt er gerekend?
kg en .
kg en , dus .
Welke waarden hebben de twee waarschuwingsgrenzen?
In hoeveel procent van de metingen worden die grenzen maximaal overschreden?
Bovenste waarschuwingsgrens: .
Onderste waarschuwingsgrens: .
Volgens de vuistregels in % van de metingen.
Welke meting is onacceptabel en vereist onmiddellijke actie?
Meting 8, daarbij wordt de onderste actiegrens behoorlijk overschreden.
Een fabrikant van erwtensoep stopt daar % rookworst in met een standaardafwijking van .
Ter controle wordt het percentage rookworst regelmatig nagemeten. Hier zie je van die metingen.

Teken hierbij een Shewhartkaart.
Zie figuur.
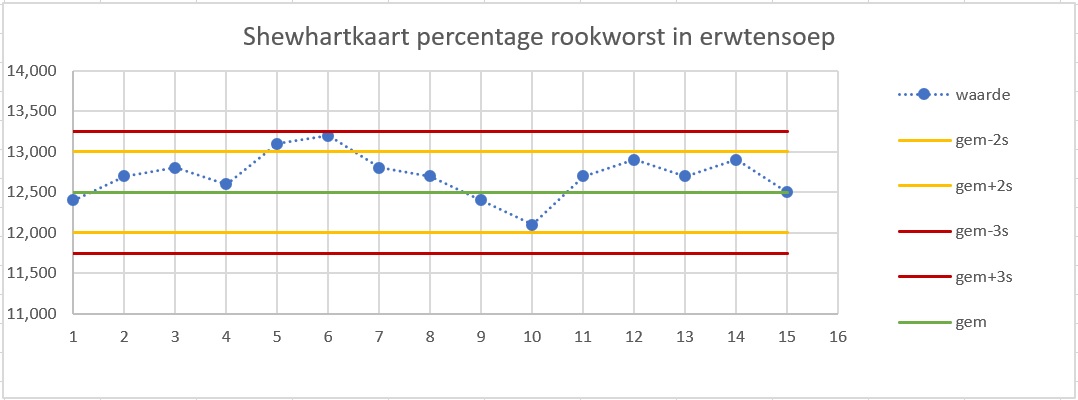
De -regel wordt overtreden als er twee metingen zijn die meer dan afwijken van het gemiddelde. Bij welke metingen is dat het geval.
Bij metingen 5 en 6.
Een controlekaart, of Shewhartkaart, kun je zelf maken met behulp van Excel.
Bekijk daarbij deze Shewhartkaart nitraatconcentratie.
Die kaart is als volgt gemaakt:
Stel eerst en van je metingen vast.
Maak de kolommen zoals die in het bestand staan, vul op de daarvoor bestemde plekken de juiste waarden van en in, laat de gele kolom leeg.
Selecteer alle kolommen inclusief hun kopjes en kies bij Invoegen voor een Spreidingsdiagram met rechte lijnen.
Werk vervolgens aan de opmaak, bijvoorbeeld de kleuren van de en de lijnen.
Je kunt natuurlijk ook de bijgevoegde Shewhartkaart gebruiken en de gegevens en instellingen van de assen aanpassen...
In plaats van de metingen nummeren, kun je ook tijdstippen neerzetten waarop je elke meting hebt gedaan.